Integrales Triples Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Regiones en el Espacio

Definición:

Una región \(W\subset \mathbb{R}^{3} \) es de tipo I si existen una región \(D \) en el plano \( XY \) de tipo 1 o 2 y dos funciones continuas \( \psi _{1},\psi _{2}:D\longrightarrow \mathbb{R} \) tales que \begin{equation*} W=\left\{ \left( x,y,z \right) \,\left\vert \,\left( x,y\right) \in D,\quad \psi _{1}\left( x,y\right) \leq z\leq \psi _{2}\left( x,y\right) \right. \right\} . \end{equation*} Si \(\psi _{1}\left( x,y\right) =\psi _{2}\left( x,y\right) , \) entonces \( \left( x,y\right) \in \partial D, \) es decir, si las superficies \(z=\psi _{1}\left( x,y\right) \) y \(z=\psi _{2}\left( x,y\right) \) se intersectan, lo hacen sólo en \(\partial D. \)

• Si \(D \) es de tipo 1, entonces existen dos funciones continuas \(\phi _{1},\phi _{2}:\left[ a,b\right] \longrightarrow \mathbb{R} \) \begin{equation*} D=\left\{ \left( x,y\right) \,\,\left\vert \,\,x\in \left[ a,b\right] ,\quad \phi _{1}\left( x\right) \leq y\leq \phi _{2}\left( x\right) \right. \right\} \end{equation*} y por tanto, \begin{equation} W=\left\{ \left. \left( x,y,z\right) \right\vert \,a\leq x\leq b,\quad \phi _{1}\left( x\right) \leq y\leq \phi _{2}\left( x\right) ,\quad \psi _{1}\left( x,y\right) \leq z\leq \psi _{2}\left( x,y\right) \right\} \label{1}\tag{1} \end{equation}
• Si \(D \) es de tipo 2, entonces existen dos funciones continuas \(\phi _{1},\phi _{2}:\left[ c,d\right] \longrightarrow \mathbb{R} \) tales que \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ c,d\right] ,\quad \phi _{1}\left( y\right) \leq x\leq \phi _{2}\left( y\right) \right. \right\} \end{equation*} y por tanto,

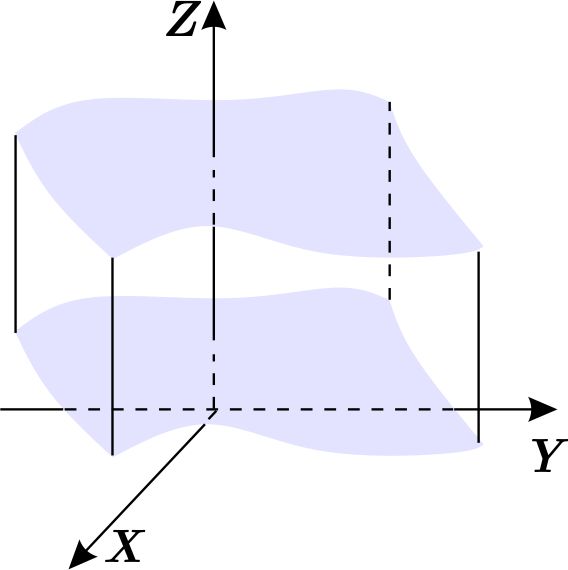
Definición:

Una región \(W\subset \mathbb{R}^{3} \) es de tipo II si puede expresarse en la forma (\ref{1}) o (\ref{2}) intercambiando los papeles de \( x \) y \(z \) , es decir, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,a\leq z\leq b,\quad \phi _{1}\left( z\right) \leq y\leq \phi _{2}\left( z\right) ,\quad \psi _{1}\left( z,y\right) \leq x\leq \psi _{2}\left( z,y\right) \right. \right\} , \end{equation*} o bien, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,c\leq y\leq d,\quad \phi _{1}\left( y\right) \leq z\leq \phi _{2}\left( y\right) ,\quad \psi _{1}\left( z,y\right) \leq x\leq \psi _{2}\left( z,y\right) \right. \right\} \end{equation*}

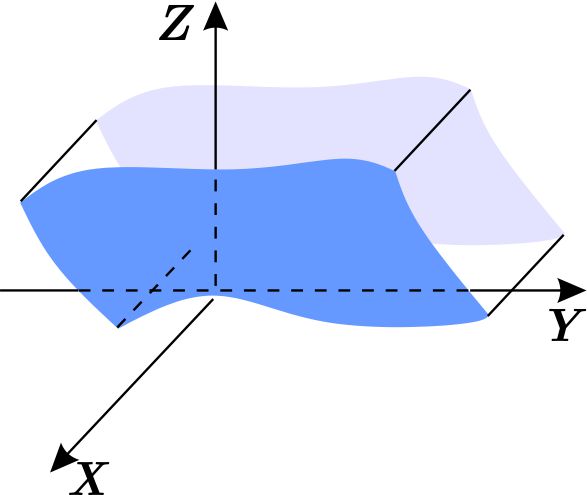
Definición:

Análogamente \(W \) es del tipo III si puede expresarse en la forma (\ref {1}) o (\ref{2}) intercambiando los papeles de \(y \) y \(z \) , es decir, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,a\leq x\leq b,\quad \phi _{1}\left( x\right) \leq z\leq \phi _{2}\left( x\right) ,\quad \psi _{1}\left( x,z\right) \leq y\leq \psi _{2}\left( x,z\right) \right. \right\} , \end{equation*} o bien, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,c\leq z\leq d,\quad \phi _{1}\left( z\right) \leq x\leq \phi _{2}\left( z\right) ,\quad \psi _{1}\left( x,z\right) \leq y\leq \psi _{2}\left( x,z\right) \right. \right\} . \end{equation*}

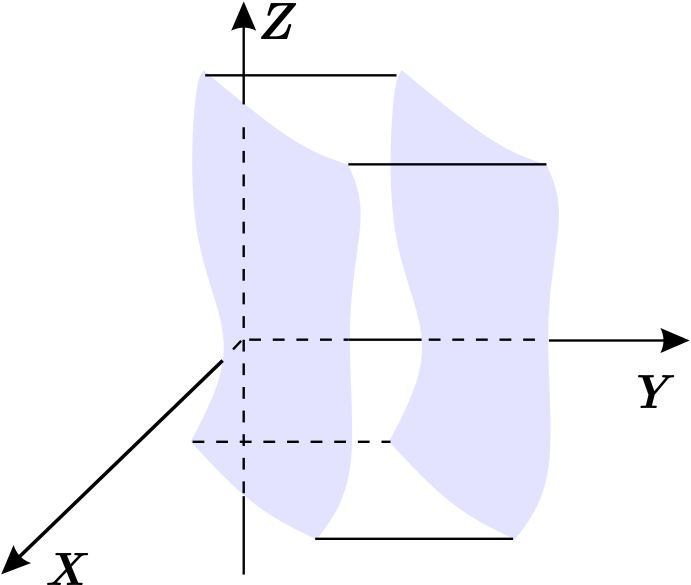
Definición:

Una región \(W\subset \mathbb{R}^{3} \) es de tipo IV si es de tipo I, II, III.

Observaciones:

En las regiones del espacio de

• tipo I, las partes superior e inferior son superficies \(z=f\left( x,y\right) . \)
• tipo II, el frente y la parte posterior son superficies \(x=f\left( z,y\right) . \)
• tipo III, las partes derecha e izquierda son superficies \(y=f\left( x,z\right) . \)

Ejemplos

1. Esfera
2. Paraboloide
3. Cono
4. Hiperboloide

Ejercicios

1. Describe la región \(W \) limitada por el paraboloide \(z=x^{2}+y^{2} \) con \(z\in \left[ 0,9\right] \) como una región del tipo I.
   
   
2. Describe la región \(W \) limitada por el paraboloide circular \( y=\left( \dfrac{x}{2}\right) ^{2}+\left( \dfrac{z}{2}\right) ^{2} \) con \(y\in \left[ 0,8\right] \) como una región del tipo III.
   
   
3. Describe la región \(W \) limitada por la sección de hiperboloide \( z=\sqrt{x^{2}+y^{2}+1} \) y el plano \(z=3 \) como una región del tipo I.
   
   
4. Describe la región \(W \) limitada por los planos \( x=0,y=0,x=-2,y=2,z=1 \) y \(y+z-5=0 \) , como una región del tipo III.