Integrales Triples Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Regiones en el espacio

Describe la región \(W \) limitada por el cono \(z=-\sqrt{x^{2}+y^{2}} \) con \(z\in \left[ -5,0\right] \) como una región del tipo I.

Solución:

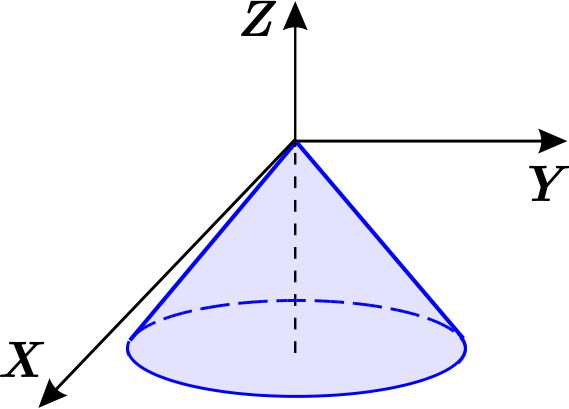
Si consideramos \(z=-5 \) en la ecuación, tenemos \(-\sqrt{x^{2}+y^{2}}=-5, \) tenemos \begin{equation*} x^{2}+y^{2}=25, \end{equation*} es decir, la tapa del cono es un disco. La proyección de \(W \) sobre \(XY \) coincide con la proyección de dicho disco. Así, la región \(D \) en el plano \(XY \) es un círculo con centro en el origen y radio 5. \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-5\leq x\leq 5,\quad -\sqrt{ 25-x^{2}}\leq y\leq \sqrt{25-x^{2}}\right. \right\} . \end{equation*} La región \(W \) es \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\quad -5\leq z\leq -\sqrt{x^{2}+y^{2}}\right. \right\} , \end{equation*} es decir, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,-5\leq x\leq 5,\quad -\sqrt{ 25-x^{2}}\leq y\leq \sqrt{25-x^{2}},\quad -5\leq z\leq -\sqrt{x^{2}+y^{2}} \right. \right\} . \end{equation*}