Integrales Triples Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Regiones en el espacio

Describe la región \(W \) limitada por la sección de hiperboloide \( z=\sqrt{x^{2}+y^{2}+1} \) y el plano \(z=3 \) como una región del tipo III.

Solución:

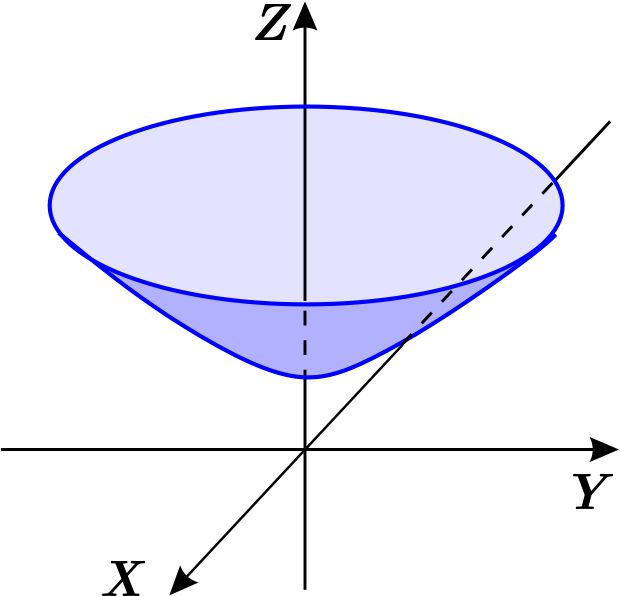
Si consideramos \(y=0 \) en la ecuación del hiperboloide, tenemos \begin{equation*} z=\sqrt{x^{2}+1}, \end{equation*} que es la rama superior de una hipérbola en el plano \(XZ \)

Al hacer \(z=3 \) en esta última ecuación tenemos \begin{eqnarray*} 3 &=&\sqrt{x^{2}+1}, \\ x^{2} &=&8. \end{eqnarray*} O sea, la intersección de la hipérbola \(z=\sqrt{x^{2}+1} \) y la recta \( z=3 \) en el plano \(XZ \) son los puntos \(\left( -2\sqrt{2},3\right) \) y \( \left( 2\sqrt{2},3\right) . \) La proyección de \(W \) sobre \(XZ \) es

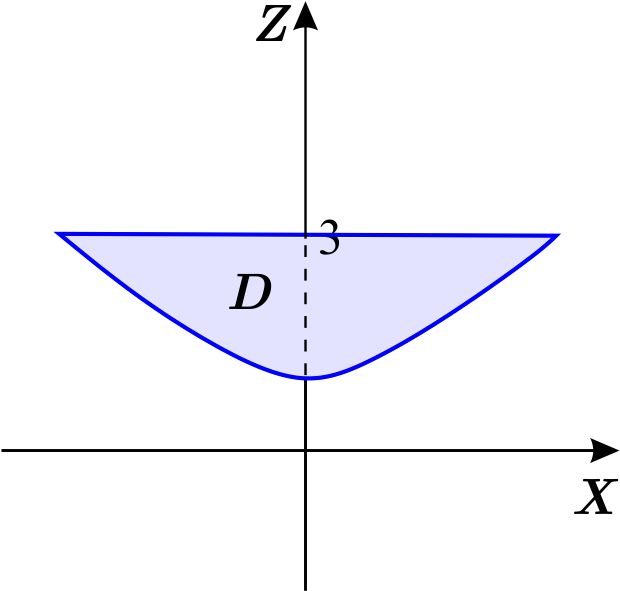
Así, la región \(D \) en el plano \(XZ \) es de tipo 3. Si escribimos \(D \) como de tipo \(1, \) tenemos: \begin{equation*} D=\left\{ \left( x,z\right) \,\left\vert \,-2\sqrt{2}\leq x\leq 2\sqrt{2} ,\quad \sqrt{x^{2}+1}\leq z\leq 3\right. \right\} . \end{equation*} La región \(W \) es \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,z\right) \in D,\quad -\sqrt{z^{2}-x^{2}-1}\leq y\leq \sqrt{z^{2}-x^{2}-1}\right. \right\} \\ &=&\left\{ \left( x,y,z\right) \,\left\vert \,-2\sqrt{2}\leq x\leq 2\sqrt{2} ,\quad \sqrt{x^{2}+1}\leq z\leq 3,\quad -\sqrt{z^{2}-x^{2}-1}\leq y\leq \sqrt{z^{2}-x^{2}-1}\right. \right\} . \end{eqnarray*} Si escribimos \(D \) como de tipo \(2, \) tenemos: \begin{equation*} D=\left\{ \left( x,z\right) \,\left\vert \,1\leq z\leq 3,\quad -\sqrt{z^{2}-1 }\leq x\leq \sqrt{z^{2}-1}\right. \right\} . \end{equation*} La región \(W \) es \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,z\right) \in D,\quad -\sqrt{z^{2}-x^{2}-1}\leq y\leq \sqrt{z^{2}-x^{2}-1}\right. \right\} \\ &=&\left\{ \left( x,y,z\right) \,\left\vert \,1\leq z\leq 3,\quad -\sqrt{ z^{2}-1}\leq x\leq \sqrt{z^{2}-1},\quad -\sqrt{z^{2}-x^{2}-1}\leq y\leq \sqrt{z^{2}-x^{2}-1}\right. \right\} . \end{eqnarray*}