Integrales Triples Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Regiones en el espacio

Describe la esfera \(W \) con centro en el origen y radio 4 como una región del tipo I.

Solución:

La esfera con centro en el origen y radio 4 tiene ecuación \begin{equation*} x^{2}+y^{2}+z^{2}\leq 16. \end{equation*}

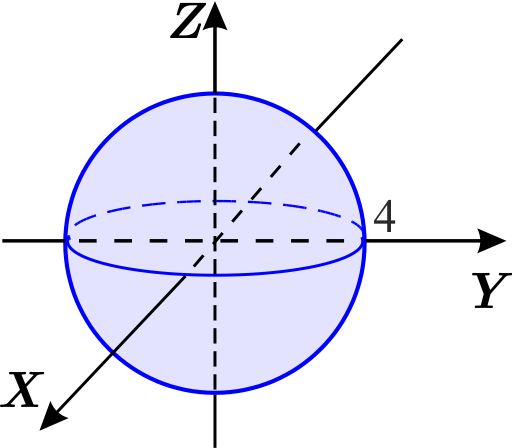
Primero describimos el conjunto \(D \) en el plano \(XY \) . La proyección de la esfera sobre \(XY \) es el círculo con centro en el origen y radio 4 \begin{equation*} D=\left\{ \left. \left( x,y\right) \,\right\vert \,x^{2}+y^{2}\leq 16\right\} , \end{equation*} Para determinar el intervalo en el que varía \(x, \) consideramos \(y=0, \) es decir, \begin{eqnarray*} x^{2} &\leq &16 \\ \left\vert x\right\vert &\leq &4, \end{eqnarray*} de donde, \begin{equation*} -4\leq x\leq 4. \end{equation*} Ahora consideramos la inecuación \(x^{2}+y^{2}\leq 16 \) y despejamos \(y \) \begin{eqnarray*} x^{2}+y^{2} &\leq &16 \\ y^{2} &\leq &16-x^{2} \\ \left\vert y^{2}\right\vert &\leq &\sqrt{16-x^{2}}, \end{eqnarray*} es decir, \begin{equation*} -\sqrt{16-x^{2}}\leq y\leq \sqrt{16-x^{2}} \end{equation*} así, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}}\right. \right\} . \end{equation*} Para determinar \(\psi _{1} \) y \(\psi _{2}, \) despejamos \(z \) de \( x^{2}+y^{2}+z^{2}\leq 16 \) , es decir \begin{eqnarray*} x^{2}+y^{2}+z^{2} &\leq &16 \\ z^{2} &\leq &16-x^{2}-y^{2} \\ \left\vert z\right\vert &\leq &\sqrt{16-x^{2}-y^{2}}, \end{eqnarray*} de donde, \begin{equation*} -\sqrt{16-x^{2}-y^{2}}\leq z\leq \sqrt{16-x^{2}-y^{2}}. \end{equation*} Por tanto, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\quad - \sqrt{16-x^{2}-y^{2}}\leq z\leq \sqrt{16-x^{2}-y^{2}}\right. \right\} , \end{equation*} es decir, \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}},\quad -\sqrt{16-x^{2}-y^{2}}\leq z\leq \sqrt{16-x^{2}-y^{2}}\right. \right\} . \end{equation*} Como \(D \) es un conjunto de tipo 3, podemos representar a \(D \) como de tipo 2, y escribir a \(W \) del modo siguiente. \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,-4\leq y\leq 4,\quad -\sqrt{ 16-y^{2}}\leq x\leq \sqrt{16-y^{2}},\quad -\sqrt{16-x^{2}-y^{2}}\leq z\leq \sqrt{16-x^{2}-y^{2}}\right. \right\} . \end{equation*}