Coordenadas Cilíndricas y Esféricas Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Coordenadas Cilíndricas

Definición:

Partimos de un sistema cartesiano \(XYZ \) con origen \(O. \) En el plano \(XY \) escojamos el origen \( O \) como polo, al semieje \( OX \) como eje polar y la orientación positiva de giro como aquella que lleva a coincidir al semieje \( OX \) con el \( OY \) mediante un giro de \( 90^{\circ }. \) Dado un punto \( P \) en el espacio con coordenadas rectangulares \( \left( x,y,z\right) \) tomamos \( \left( r,\theta \right) \) como unas coordenadas polares de la proyección \( P^{\prime }\left( x,y,0\right) \) de \( P \) sobre el plano \( XY. \) Los números reales de la tercia \( \left( r,\theta ,z\right) \) son llamados unas coordenadas cilíndricas de \( P. \)

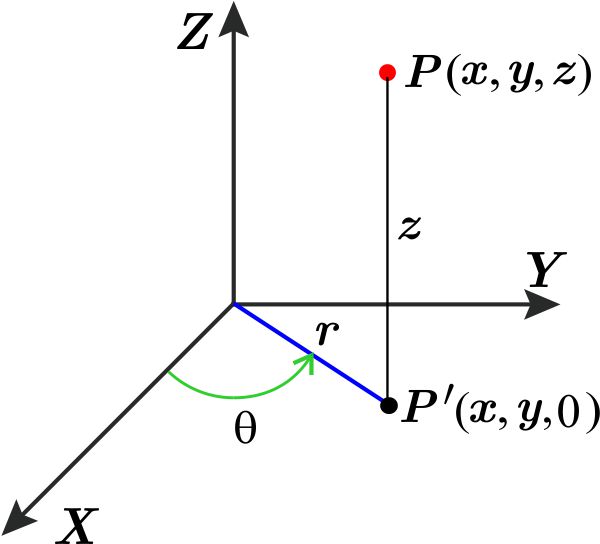
La coordenada \( z \) es llamada altura o altitud.

En particular, para \( \left( x,y\right) \neq \left( 0,0\right) , \) los reales \( r \) y \( \theta \) pueden ser tomados como las coordenadas polares principales de \( P^{\prime }\left( x,y,0\right),\) en cuyo caso \begin{eqnarray} &&r=\sqrt{x^{2}+y^{2}}>0\text{ y} \notag \\ \theta &=&\left\{ \begin{array}{ll} \arctan \dfrac{y}{x} & \text{si }x>0\text{ y }y\geq 0 \\ \pi +\arctan \dfrac{y}{x} & \text{si }x < 0 \\ 2\pi +\arctan \dfrac{y}{x} & \text{si }x>0\text{ y }y < 0 \\ \dfrac{\pi }{2} & \text{si }x=0\text{ y }y>0 \\ -\dfrac{\pi }{2} & \text{si }x=0\text{ y }y < 0 \end{array} \right. \label{1}\tag{1} \end{eqnarray} Para \( \left( x,y\right) =\left( 0,0\right) \) , podemos escoger \( \theta \) arbitrariamente, por ejemplo \( \theta =0. \)

La coordenada \( r \) es llamada la coordenada radial o radio y \( \theta \) la coordenada acimutal o acimut.

Notamos que cada punto \( P \) tiene una infinidad de coordenadas cilíndricas, pues cada punto \( \left( x,y\right) \) del plano \( XY \) tiene una infinidad de coordenadas polares. Si \( \left( r,\theta \right) \) son las coordenadas polares principales de \( P^{\prime }(x,y,0) \) en \( XY \), entonces \( \left( r,\theta +2n\pi ,z\right) \) y \( \left( -r,\theta +\pi +2n\pi ,z\right) \) con \( n\in \mathbb{Z} \) son también coordenadas cilíndricas de \( P\left( x,y,z\right) . \)

Si \( \left( r,\theta ,z\right) \) son cualesquiera coordenadas cilíndricas de \( P\left( x,y,z\right) , \) entonces \begin{eqnarray*} x &=&r\cos \theta , \\ y &=&r\ \text{sen}\ \theta \\ z &=&z \end{eqnarray*} y se cumple la igualdad \begin{equation*} x^{2}+y^{2}=r^{2}. \end{equation*} A cualquier tercia de reales \( \left( r,\theta ,z\right) \) le podemos hacer corresponder un único punto \( P \) que tiene por coordenadas cilíndricas a dicha tercia. Simplemente localizamos en el sistema cartesiano \( XYZ \) el punto \( P \) con coordenadas rectangulares \( \left( r\cos \theta , r \ \text{sen}\ \theta ,z\right) . \)

Ejemplos

1. Encuentra las coordenadas rectangulares del punto \( P \) cuyas coordenadas cilíndricas son \( \left( r,\theta ,z\right) =\left( 5,\dfrac{ \pi }{4},-4\right) . \)

   Solución:

   \begin{eqnarray*} x &=&r\cos \theta =5\cos \dfrac{\pi }{4}=5\left( \dfrac{1}{\sqrt{2}}\right) = \dfrac{5}{\sqrt{2}} \\ y &=&r\ \text{sen}\ \theta =5\ \text{sen}\ \dfrac{\pi }{4}=5\left( \dfrac{1}{ \sqrt{2}}\right) =\dfrac{5}{\sqrt{2}} \\ z &=&-4. \end{eqnarray*} Por lo tanto, las coordenadas rectangulares del punto \( P \) son \( \left( \dfrac{ 5}{\sqrt{2}},\dfrac{5}{\sqrt{2}},-4\right) . \)

2. Encuentra unas coordenadas cilíndricas del punto \( P \) cuyas coordenadas rectangulares son \( \left( x,y,z\right) =\left( -1,1,-6\right) . \)

   Solución:

   Las coordenadas polares principales de la proyección \( P^{\prime }\left( -1,1,0\right) \) de \( P \) sobre \( XY \) son (ver \ref{1}) \begin{equation*} r=\sqrt{2} \end{equation*} y \begin{eqnarray*} \theta &=&\pi +\arctan \dfrac{y}{x} \\ &=&\pi +\arctan(-1) \\ &=&\pi -\frac{1}{4}\pi =\frac{3}{4}\pi . \end{eqnarray*} Entonces \( \left( \sqrt{2},\dfrac{3}{4}\pi ,-6\right) \) son coordenadas cilíndricas de \( P. \)

Ejercicios

1. Encontrar las coordenadas cilíndricas de los puntos que tienen coordenadas rectangulares

   1. \( \left( 1,-1,100\right) . \)

   2. \( \left( \sqrt{3},1,\sqrt[3]{5}\right) . \)

   3. \( \left( 4,-2,\sqrt{7}\right) . \)

   4. \( \left( -\dfrac{\sqrt{3}}{2},\dfrac{1}{2},-e\right) . \)

   5. \( \left( -2,-1,-e\right) . \)

2. Encontrar las coordenadas rectangulares de los puntos que tienen coordenadas cilíndricas

   1. \( \left( 2,\pi ,-1\right) . \)

   2. \( \left( 8,\dfrac{\pi }{2},\dfrac{1}{4}\right) . \)

   3. \( \left( \sqrt{3},\dfrac{\pi }{4},\pi \right) . \)

   4. \( \left( 1,\dfrac{\pi }{3},-24\right) . \)

   5. \( \left( \dfrac{\pi }{2},0,-1\right) . \)

Ecuaciones cilíndricas

Se dice que una superficie \( S \) tiene por ecuación cartesiana a una ecuación del tipo \begin{equation*} F\left( x,y,z\right) =0 \end{equation*} si cada uno de sus puntos y sólo ellos tienen coordenadas rectangulares \( \left( x,y,z\right) \) que satisfacen esa ecuación, donde \( F \) es una función real.

En tanto que, se dice que una superficie \( S \) tiene por ecuación cilíndrica una ecuación del tipo \begin{equation} G\left( r,\theta ,z\right) =0 \label{eccilingral}\tag{2} \end{equation} si cada uno de sus puntos y sólo ellos tienen coordenadas cilíndricas \( \left( r,\theta ,z\right) \) que satisfacen dicha ecuación, donde \( G \) es una función real.

En muchas ocasiones \( G\left( r,\theta ,z\right) =z-f\left( r,\theta \right) \) , donde \( f \) es una función real. En tales casos la ecuación cilíndrica (\ref{eccilingral}) se transforma en \begin{equation*} z=f\left( r,\theta \right) . \end{equation*} Una superficie en el espacio tiene asociada una ecuación cartesiana y también una cilíndrica.

El paso de una a otra se logra mediante el uso de las ecuaciones \begin{equation*} x^{2}+y^{2}=r^{2},\quad \ \text{sen}\ \theta =\dfrac{y}{\sqrt{x^{2}+y^{2}}} ,\quad \cos \theta =\dfrac{x}{\sqrt{x^{2}+y^{2}}}, \label{I}\tag{3} \end{equation*} y \begin{equation} x=r\cos \theta ,\quad y=r\ \text{sen}\ \theta \quad \text{y}\quad z=z. \label{4}\tag{4} \end{equation}

Ejemplos

1. Paraboloide

2. Cilindro

3. Cono

4. Cilindro Parabólico

Ejercicios

1. Encontrar la ecuación rectangular correspondiente a la ecuación cilíndrica que se indica.

   1. \( r=r_{0}, \) donde \( r_{0}>0 \) (cilindro circular recto).

   2. \( \theta =\theta _{0}, \) donde \( 0\leq \theta _{0}<\pi \) (plano).

   3. \( z=z_{0}, \) donde \( z_{0}\in \mathbb{R} \) (plano).

   4. \( r=5\cos \theta \) (cilindro circular recto y el origen).

   5. \( z^{2}=r^{2}\cos 2\theta \) (paraboloide hiperbólico).

2. Se perfora una esfera centrada en el origen de radio \( 3 \) usando un cilindro de radio \( 2, \) del modo que se indica en el siguiente corte lateral.
   

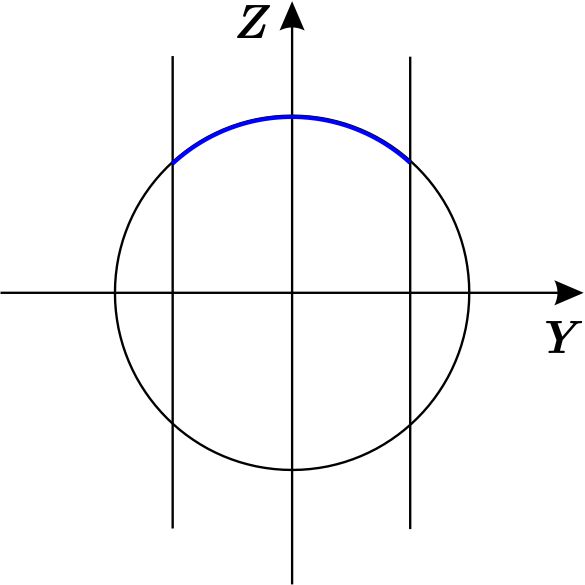
   Describir el casquete superior \( C \) eliminado usando coordenadas cilíndricas.

3. Escribe la ecuación cilíndrica del paraboloide elíptico con ecuación cartesiana \( z=2y^{2}+3x^{2}. \)

4. Escribe la ecuación cilíndrica de las superficies cuadráticas, cuyas ecuaciones cartesianas son de los siguientes tipos:

   1. Elipsoide: \( \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{ c^{2}}=1. \)

   2. Paraboloide hiperbólico: \( \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}} =z. \)

   3. Hiperboloide de una hoja: \( \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}- \dfrac{z^{2}}{c^{2}}=1. \)

   4. Hiperboloide de dos hojas: \( \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}- \dfrac{z^{2}}{c^{2}}=1. \)

   5. Cono elíptico: \( \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}-\dfrac{ z^{2}}{c^{2}}=0 \) (si \( a^{2}=b^{2}, \) entonces es llamado cono circular).

5. Encuentra las ecuaciones cilíndricas que determinan la intersección de las superficies con ecuaciones cartesianas \( z-4=x^{2}+y^{2} \) y \( z^{2}=16x^{2}+16y^{2}. \)

Transformación cilíndrica

Ejemplo

Determinar las superficies \( S_{ci} \) y \( S_{ca} \) definidas por la ecuación \(r=a \), con \( a>0 \), cuando ésta se interpreta como una ecuación cilíndrica y cuando se le considera como una ecuación cartesiana, respectivamente.

Solución:

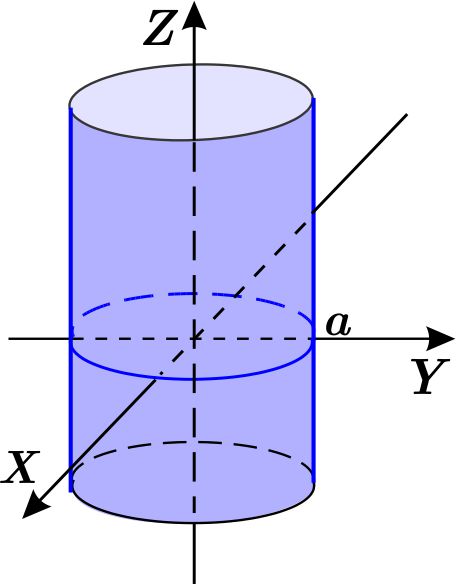
Los puntos del sistema \( XYZ \) cuyas coordenadas cilíndricas \( \left( r,\theta ,z\right) \) satisfacen \( r=a, \) son los del cilindro circular recto con base en el círculo con centro en el origen y radio \( a. \) O sea, este cilindro es la superficie \( S_{ci} \) en el sistema \( XYZ \) que tiene ecuación cilíndrica \( r=a. \)

Por otra parte, los puntos del sistema cartesiano \( R\Theta Z \) cuyas coordenadas \( \left( r,\theta ,z\right) \) satisfacen \( r=a, \) son los del plano \(r=a \) en dicho sistema. O sea, este plano es la superficie \( S_{ca} \) en el sistema \( R\Theta Z \) que tiene ecuación cartesiana \( r=a. \)

Mediante la función \begin{equation*} T_{c}\left( r,\theta ,z\right) =\left( r\cos \theta ,r\ \text{sen}\ \theta ,z\right) \end{equation*} del sistema \( R\Theta Z \) en \( XYZ \), llamada la transformación cilíndrica, la superficie \( S_{ca} \) se transforma en \( S_{ci}. \)

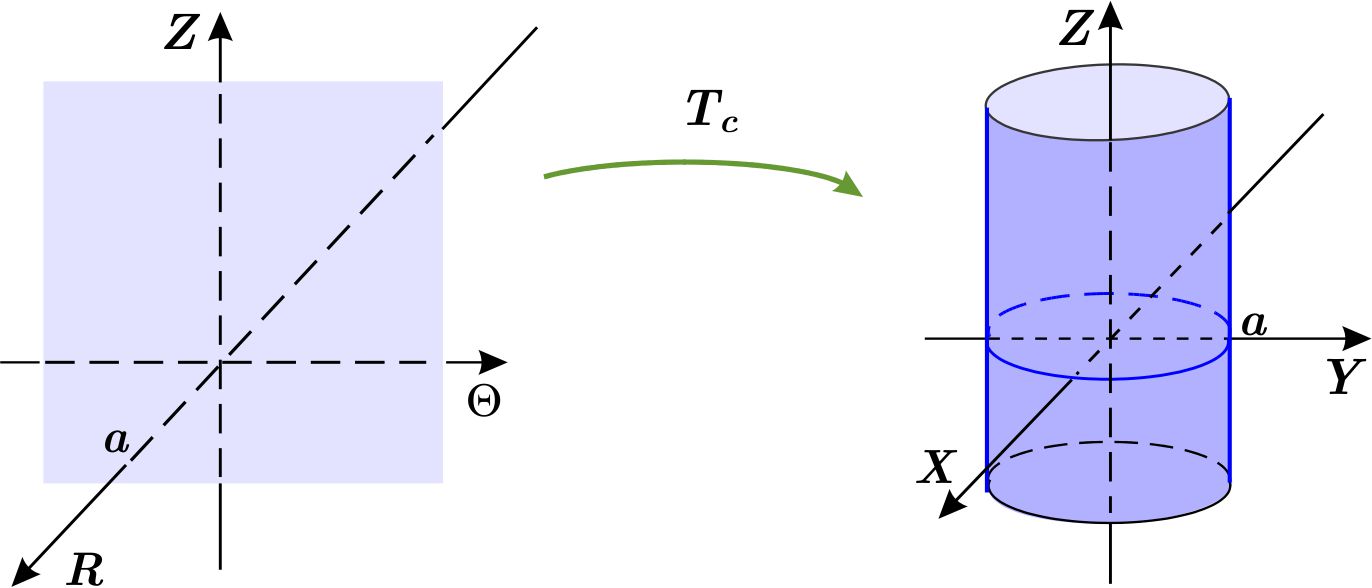
En general, supongamos que \( W \) es una región en el sistema \( XYZ \) y \( W_{1} \) es una colección formada por coordenadas cilíndricas de todos los puntos de \( W, \) entonces \( W_{1} \) representa una región del sistema \( R\Theta Z \) y \begin{equation*} T_{c}\left( W_{1}\right) =W. \end{equation*} La transformación cilíndrica es inyectiva y de clase \( C^{1} \) en la región \( \left( 0,\infty \right) \times \left( 0,2\pi \right) \times \mathbb{R} \) del sistema \( R\Theta Z. \) Esta región es el interior de \( \left[ 0,\infty \right) \times \left[ 0,2\pi \right] \times \mathbb{R}. \)