Coordenadas Cilíndricas y Esféricas Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Obtén la ecuación cilíndrica del paraboloide \( z=x^{2}+y^{2}-3y. \)

Solución:

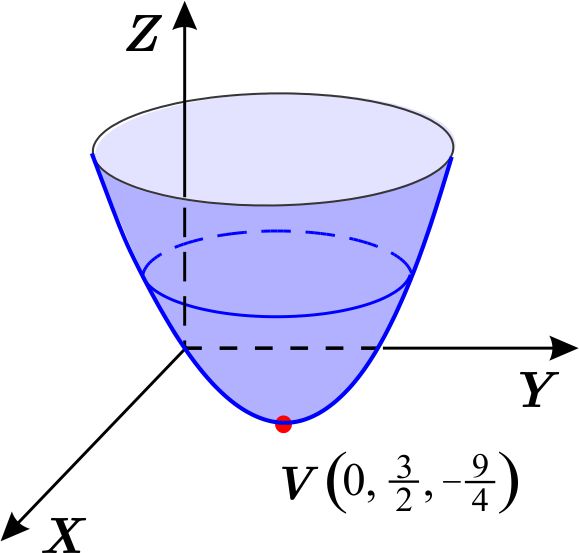
Haciendo \begin{eqnarray*} x &=&r\cos \theta \\ y &=&r\ \text{sen}\ \theta \\ z &=&z, \end{eqnarray*} tenemos \begin{eqnarray*} z &=&r^{2}\cos ^{2}\theta +r^{2}\ \text{sen}^{2}\theta -3r \ \text{sen}\ \theta \\ &=&r^{2}-3r\ \text{sen}\ \theta . \end{eqnarray*} Por lo tanto, la ecuación en coordenadas cilíndricas del paraboloide es \( z=r^{2}-3r\ \text{sen}\ \theta . \)