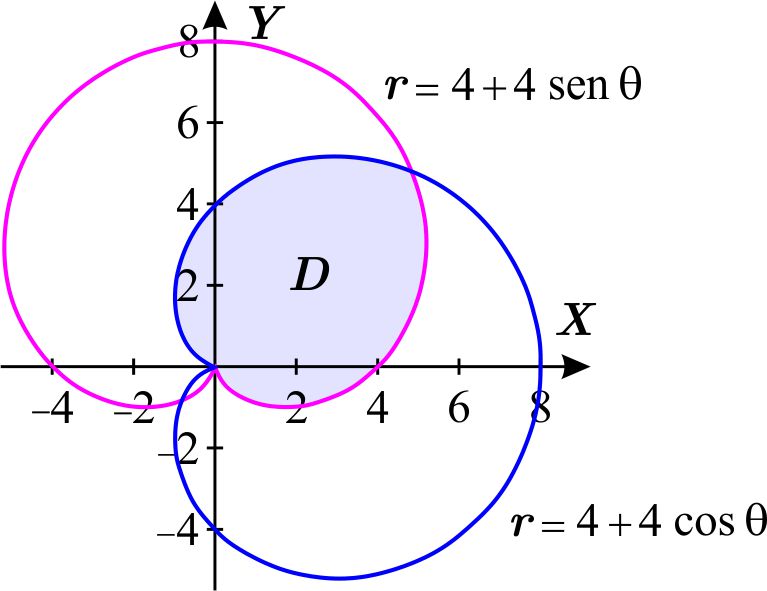
Integrales Dobles
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

 |
Integrales DoblesAngel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) |  |
En el primer caso, hablaremos del plano cartesiano \(\Theta R\) o \(R\Theta \) según si en el eje horizontal marquemos los valores de la coordenada \( \theta \) y en el vertical los de la coordenada \(r\) o viceversa. Básicamente usaremos el plano cartesiano \(\Theta R\) para graficar funciones del tipo \(r=f\left( \theta \right) . \)
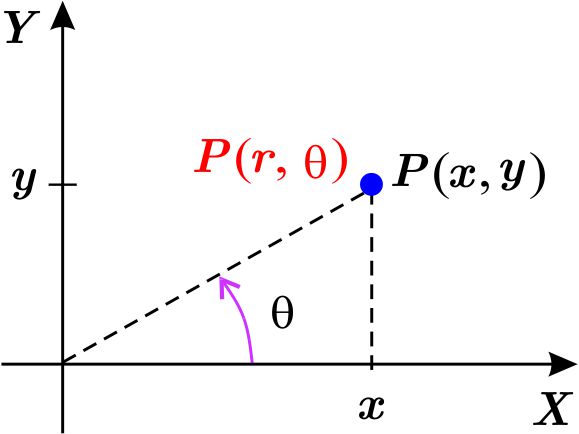
Las coordenadas polares principales son \begin{equation*} r=\sqrt{x^{2}+y^{2}}\qquad \qquad \qquad \end{equation*} y \begin{equation} \theta =\left\{ \begin{array}{ll} \arctan \left( \dfrac{y}{x}\right) & \text{si } x>0, y\geq 0 \text{ (o sea,} \left(x,y\right) \text{ en el 1er cuadrante)} \\ \arctan \left( \dfrac{y}{x}\right) +\pi & \text{si } x < 0, y\in \mathbb{R} \ \text{(o sea,} \left( x,y\right) \text{ en el 2o o 3er cuadrantes)} \\ \arctan \left( \dfrac{y}{x}\right) +2\pi & \text{si } x>0, y < 0 \ \text{(o sea,} \left( x,y\right) \text{ en el 4o cuadrante).} \\ 0 & \text{si } x=0 ~ \text{y } y=0 \\ \dfrac{\pi }{2} & \text{si } x=0 ~ \text{y } y > 0 \\ \dfrac{3\pi }{2} & \text{si } x=0 ~ \text{y } y < 0 \end{array} \right. \label{angulo} \tag{1} \end{equation} donde usamos la función $\arctan :\mathbb{R\longrightarrow }\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right) $. Lo anterior se debe a que $\arctan \dfrac{y}{x}\in \left[ 0,\dfrac{\pi }{2}\right) $ si $\dfrac{y}{x}\geq 0$ y $ \arctan \dfrac{y}{x}\in \left( -\dfrac{\pi }{2},0\right) $ si $\dfrac{y}{x} < 0.$
Observación Pudiera parecer que las relaciones \begin{equation*} x=r\cos \theta \qquad \qquad \qquad y=r\ \text{sen}\ \theta \end{equation*} sólo se satisfacen si $\left( r,\theta \right) $ son las coordenadas polares principales del punto de coordenadas cartesianas $\left( x,y\right) $ , pero esto no es así, sino que son satisfechas por cualesquiera de las coordenadas polares del punto. En efecto, si $\left( r^{\prime },\theta ^{\prime }\right) $ son unas coordenadas polares de $P\left( x,y\right) $ y $\left( r,\theta \right) $ son sus coordenadas polares principales, entonces $\left( r^{\prime },\theta ^{\prime }\right) =\left( r,\theta +2n\pi \right) $ o bien, $\left( r^{\prime },\theta ^{\prime }\right) =\left( -r,\theta +\pi +2n\pi \right) $ con $n\in \mathbb{Z}$. En cada caso tenemos: \begin{eqnarray*} x &=&r\cos \theta =r\cos \left( \theta +2n\pi \right) =r^{\prime }\cos \theta ^{\prime } \\ y &=&r\ \text{sen}\ \theta = r\ \text{sen}\ \left( \theta +2n\pi \right) =r^{\prime } \text{sen}\ \theta ^{\prime } \end{eqnarray*} o bien, \begin{eqnarray*} x &=&r\cos \theta =-r\cos \left( \theta +\pi +2n\pi \right) =r^{\prime }\cos \theta ^{\prime } \\ y &=&r\ \text{sen}\ \left( \theta +2n\pi \right) =-r\ \text{sen}\ \left( \theta +\pi +2n\pi \right) =r^{\prime }\ \text{sen}\ \theta ^{\prime }. \end{eqnarray*}
Ejemplo
Solución:
\(T_{p}\) transforma puntos del plano cartesiano \(R\Theta \) en puntos del plano cartesiano \(XY,\) es decir \begin{eqnarray*} x &=&r\cos \theta \\ y &=&r\ \text{sen}\ \theta . \end{eqnarray*} Observamos que cada punto del rectángulo \(D_{1}=\left[ 0,a\right] \times \left[ 0,2\pi \right] \) está en algún segmento de la forma \(\left\{ r_{1}\right\} \times \left[ 0,2\pi \right] \) con \(0\leq r_{1}\leq a.\)
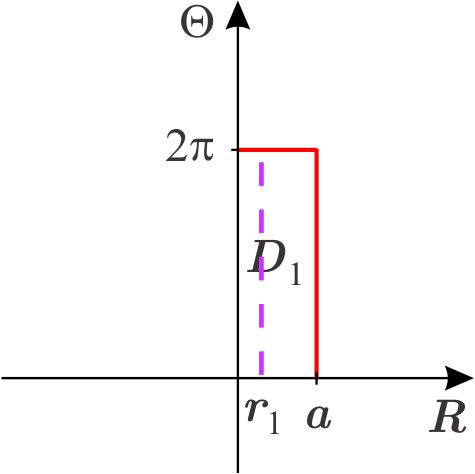
Por tanto, para encontrar la imagen de \(D_{1}\) basta encontrar las imágenes de estos segmentos y después unirlas.
Imagen de un segmento de la forma \(\left\{ r_{1}\right\} \times \left[ 0,2\pi \right] \) con \(0\leq r_{1}\leq a. \)
Si consideramos la recta \(r=r_{1}\) en el plano \(R\Theta ,\) entonces \begin{equation*} T_{p}\left( r_{1},\theta \right) =\left( r_{1}\cos \theta ,r_{1}\ \text{sen}\ \theta \right) =\left( x,y\right) . \end{equation*} De donde, \begin{eqnarray*} x^{2}+y^{2} &=&r_{1}^{2}\cos ^{2}\theta +r_{1}{}^{2}\ \text{sen}\ ^{2}\theta \\ &=&r_{1}^{2}, \end{eqnarray*} es decir, la imagen de \(\left( r_{1},\theta \right) \), para cualquier \( \theta \), es un punto de la frontera del círculo con centro en el origen y radio \(r_{1}.\)
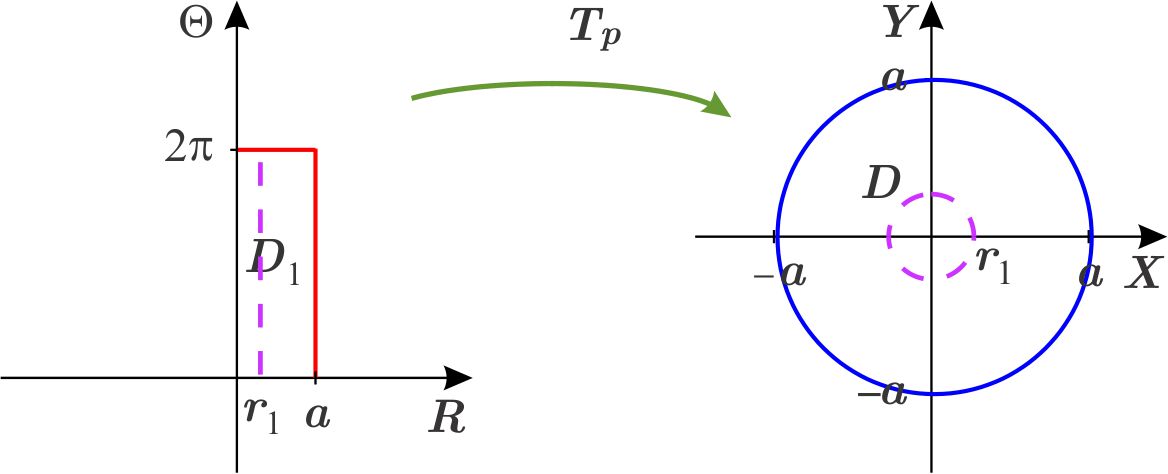
En particular, la imagen de cada segmento \(\left\{ r_{1}\right\} \times \left[ 0,2\pi \right] \) es la frontera del círculo con centro en el origen y radio \(r_{1}. \)
La unión de todas estas imágenes es el círculo con centro en el origen y radio \(a.\) Es decir, \(T_{p}\left( D_{1}\right) \) es el círculo con centro en el origen y radio \(a. \)
Su regla de correspondencia es
\begin{equation*}
T_{p}\left( r,\theta \right) =\left( r\cos \theta ,r\ \text{sen}\ \theta
\right) .
\end{equation*}
El jacobiano de la transformación polar \(T_{p}\) es:
\begin{eqnarray*}
\dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }
&=&\det \left(
\begin{array}{cc}
\cos \theta & -r\ \text{sen}\ \theta \\
\ \text{sen}\ \theta & r\cos \theta
\end{array}
\right) \\
&=&r\cos ^{2}\theta +r\ \text{sen}\ ^{2}\theta \\
&=&r.
\end{eqnarray*}
Teorema de cambio de variables para integrales dobles
Sean \(D_{1}\subset \mathbb{R}^{2}\) una región elemental y \(
L:D_{1}\longrightarrow \mathbb{R}^{2}\) una transformación inyectiva y de
clase \(C^{1}\) excepto quizás en la frontera de \(D_{1}.\) Si \(L\left(
D_{1}\right) =D\) es una región elemental y \(f:D\rightarrow \mathbb{R}, \)
es una función integrable entonces
\begin{eqnarray*}
\iint_{D}f\left( x,y\right) \,dx\,dy
&=&\iint_{D_{1}}\left( f\circ L\right) \left( u,v\right)
\left\vert \dfrac{\partial \left( x,y\right) }{\partial \left( u,v\right) }
\right\vert \,du\,dv \\
&=&\iint_{D_{1}}f\left( x\left( u,v\right) ,y\left( u,v\right)
\right) \left\vert \dfrac{\partial \left( x,y\right) }{\partial \left(
u,v\right) }\right\vert \,du\,dv
\end{eqnarray*}
donde \(L\left( u,v\right) =\left( x\left( u,v\right) ,y\left( u,v\right)
\right) \) y \(\left\vert \dfrac{\partial \left( x,y\right) }{\partial \left(
u,v\right) }\right\vert \) es el valor absoluto del jacobiano de \(L. \)
Ejemplos
Solución:
Escribimos el círculo como una región de tipo 1: \begin{equation*} D=\left\{ \left( x,y\right) \in \mathbb{R}^{2}\left\vert \,-2\leq x\leq 2,\quad \quad -\sqrt{4-x^{2}}\leq y\leq \sqrt{4-x^{2}}\right. \right\} . \end{equation*}
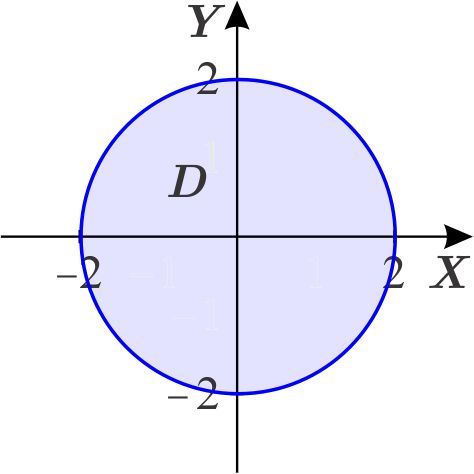
En coordenadas cartesianas la integral que hay que calcular es \begin{equation*} \int_{-2}^{2}\int_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}} }x^{2}\,dy\,dx. \end{equation*} Para calcular esta integral de una manera más fácil, usamos la transformación de coordenadas polares, es decir: \begin{equation*} T_{p}\left( r,\theta \right) =\left( r\cos \theta ,r\ \text{sen}\ \theta \right) . \end{equation*} Sabemos que la región en el plano \(R\Theta \) que corresponde a \(D\) bajo la transformación \(T_{p}\) es el rectángulo \(D_{1}=\left[ 0,2\right] \times \left[ 0,2\pi \right] \) que es una región de tipo 1.
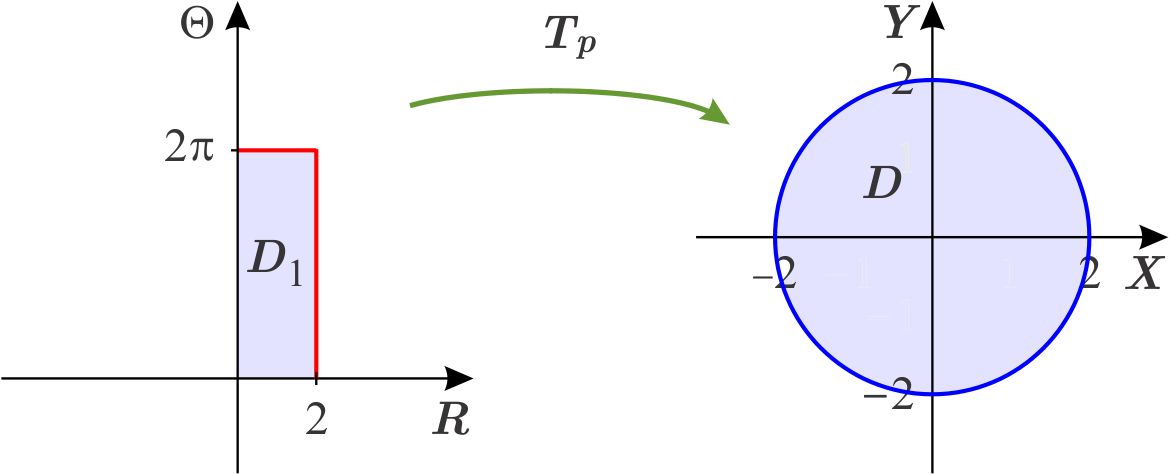
Recordamos que el jacobiano de la transformación de coordenadas polares es \begin{equation*} \dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }=r \end{equation*} y aplicamos el Teorema de cambio de variables. Entonces \begin{eqnarray*} \int_{-2}^{2}\int_{-\sqrt{4-x^{2}}}^{\sqrt{4-x^{2}} }x^{2}\,dy\,dx &=&\iint_{D_{1}}\left( f\circ T_{p}\right) \left( r,\theta \right) \left\vert \dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }\right\vert \,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{2}\left( r^{2}\cos ^{2}\theta \right) r\,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{2}r^{3}\cos ^{2}\theta \,dr\,d\theta \\ &=&\int_{0}^{2\pi }\left. \dfrac{r^{4}}{4}\cos ^{2}\theta \right\vert _{0}^{2}\,d\theta \\ &=&\int_{0}^{2\pi }4\cos ^{2}\theta \,d\theta \\ &=&4\int_{0}^{2\pi }\dfrac{1+\cos 2\theta }{2}\,d\theta \\ &=&2\left( \left. \theta +\dfrac{1}{2}\ \text{sen}\ 2\theta \right\vert _{0}^{2\pi }\right) \\ &=&4\pi . \end{eqnarray*}
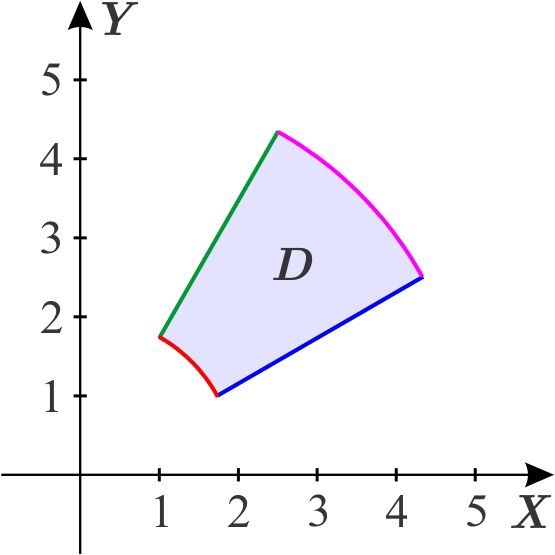
Solución:
Obtenemos las ecuaciones de las rectas en coordenadas polares: \begin{eqnarray*} y &=&\dfrac{1}{\sqrt{3}}x \\ r\ \text{sen}\ \theta &=&\dfrac{1}{\sqrt{3}}r\cos \theta \\ \tan \theta &=&\dfrac{1}{\sqrt{3}} \\ \theta &=&\dfrac{\pi }{6} \end{eqnarray*} y \begin{eqnarray*} y &=&\sqrt{3}x \\ r\ \text{sen}\ \theta &=&\sqrt{3}r\cos \theta \\ \tan \theta &=&\sqrt{3} \\ \theta &=&\dfrac{\pi }{3}. \end{eqnarray*} Como las imágenes de las rectas \(r=2\) y \(r=5 \) con \(0\leq \theta \leq 2\pi ,\) bajo la transformación \(T\) en coordenadas polares, son los círculos con centro en el origen y radios \(2\) y \(5\) respectivamente, entonces \(T\left( D_{1}\right) =D \), donde \begin{equation*} D_{1}=\left[ 2,5\right] \times \left[ \dfrac{\pi }{6},\dfrac{\pi }{3}\right] \end{equation*} que es una región de tipo \(1 \).
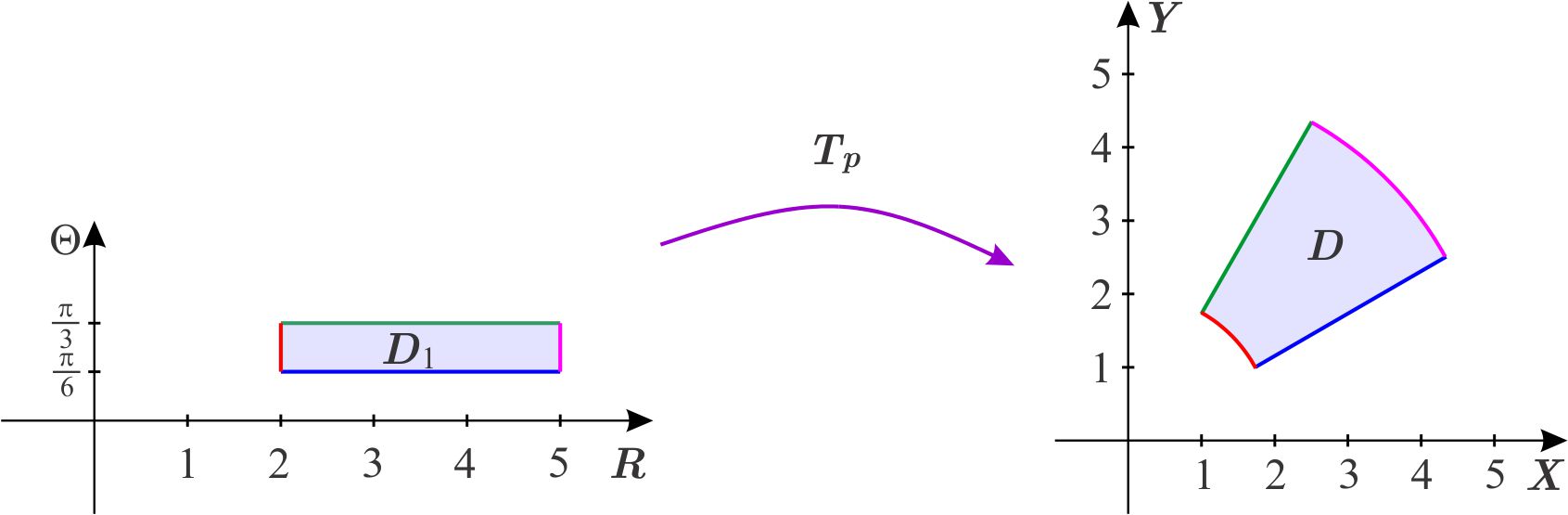
Sabemos que el jacobiano de \(T_{p} \) es \(r;\) de donde, \begin{eqnarray*} \iint_{D}\dfrac{e^{\sqrt{x^{2}+y^{2}}}}{\sqrt{x^{2}+y^{2}}}\,dy\,dx &=&\iint_{D_{1}}\left( f\circ T\right) \left( r,\theta \right) \left\vert \dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }\right\vert dr\,d\theta \\ &=&\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\int_{2}^{5} \dfrac{e^{\sqrt{r^{2}}}}{\sqrt{r^{2}}}r\,dr\,d\theta \\ &=&\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\int _{2}^{5}e^{r}\,dr\,d\theta \\ &=&\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\left. e^{r}\right\vert _{2}^{5}\,d\theta \\ &=&\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}e^{5}-e^{2}\,d\theta \\ &=&\left( e^{5}-e^{2}\right) \left( \dfrac{\pi }{3}-\dfrac{\pi }{6}\right) \\ &=&\left( e^{5}-e^{2}\right) \dfrac{\pi }{6}. \end{eqnarray*}
Solución:
\(D \) es la región \begin{equation*} D=\left\{ \left( x,y\right) \left\vert \,\left( x-2\right) ^{2}+y^{2}\leq 4\right. \right\} . \end{equation*}
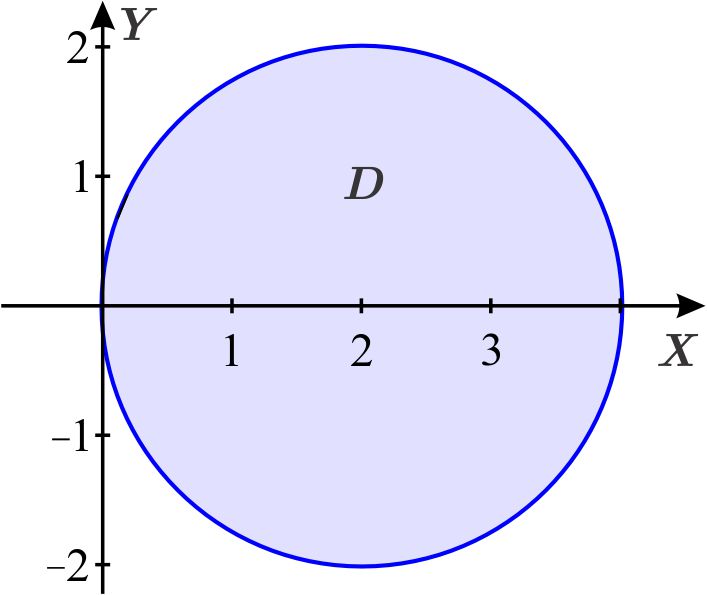
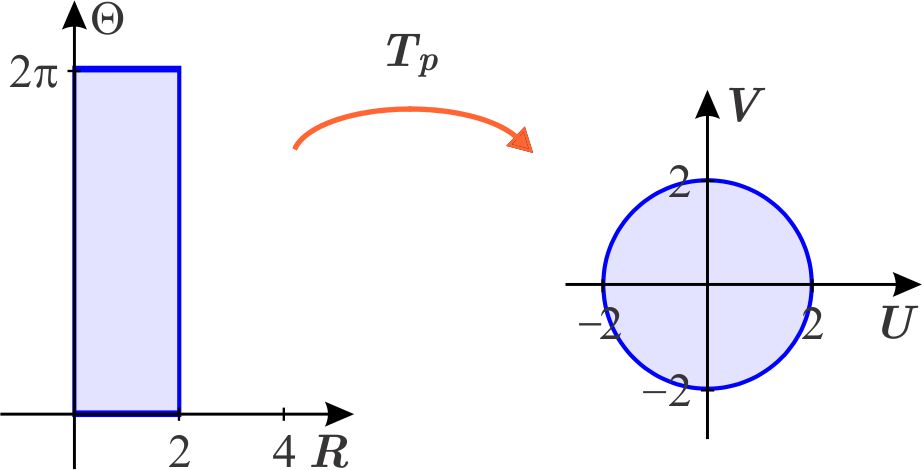
Sabemos que la transformación \(T_{p}\) de coordenadas polares envía el rectángulo \(\left[ 0,2\right] \times \left[ 0,2\pi \right] \) del plano cartesiano \(R\Theta \) en el disco con centro en el origen y radio \(2 \) en el plano cartesiano \(UV\)
Puesto que el círculo en el que queremos integrar tiene centro en el punto \(\left( 2,0\right) ,\) consideramos la traslación \(S \) \begin{eqnarray*} x &=&u+2 \\ y &=&v \end{eqnarray*} la cual transforma el círculo con centro en el origen y radio 2 en el círculo con centro en \(\left( 2,0\right) \) y radio 2.
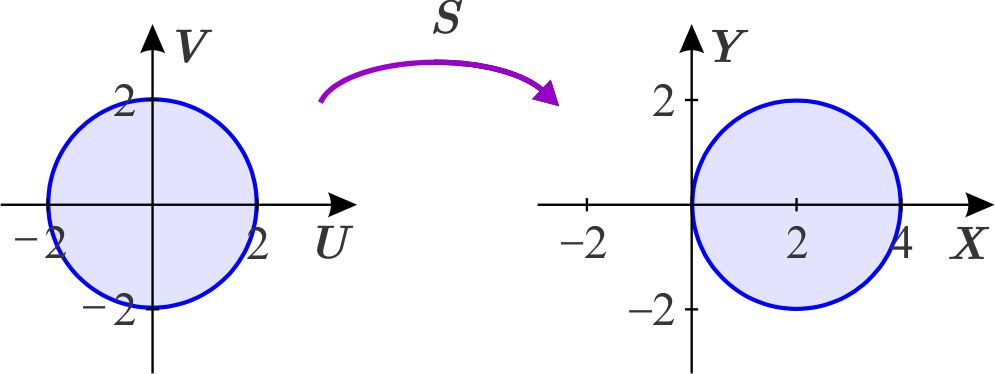
entonces, si consideramos la composición \(L=S\circ T_{p}\) de ambas transformaciones, tenemos que \(L\) transforma al rectángulo en el círculo que nos interesa.
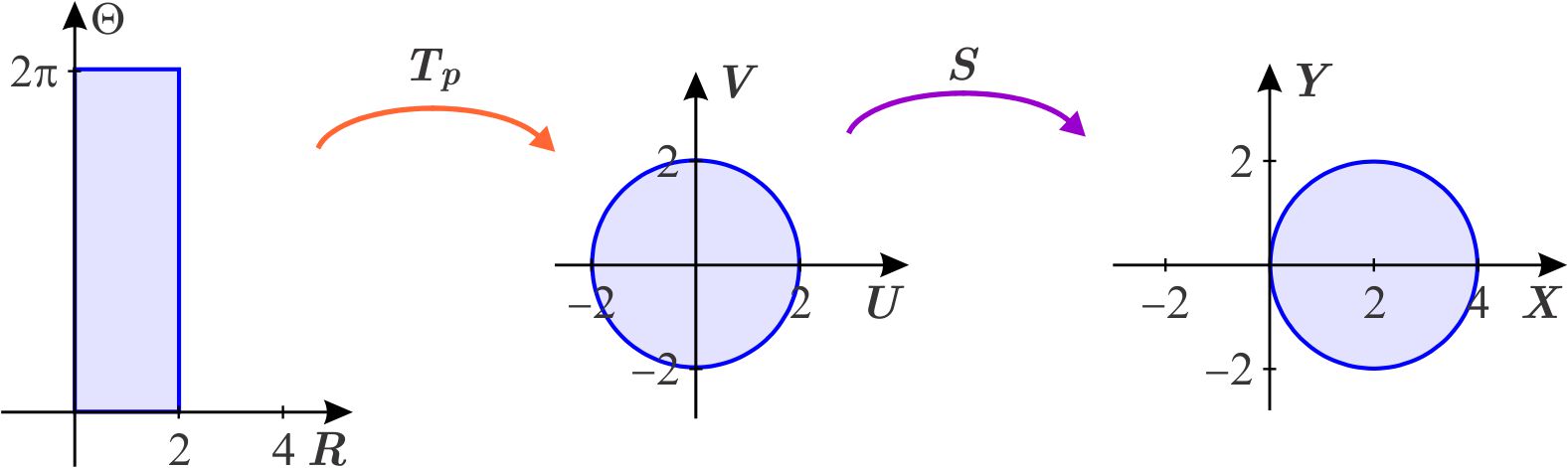
Dicha composición \(L\) tiene como regla de correspondencia \(\left( S\circ T_{p}\right) \left( r,\theta \right) =\left( r\cos \theta +2,r\ \text{sen}\ \theta \right) \) y transforma, como ya dijimos, el rectángulo \(\left[ 0,2\right] \times \left[ 0,2\pi \right] \) en el círculo con centro en \(\left( 2,0\right) \) y radio \(2. \)
Como las funciones componentes de \(L\) son \begin{eqnarray*} x &=&r\cos \theta +2 \\ y &=&r\ \text{sen}\ \theta , \end{eqnarray*} su jacobiano es:\ \begin{equation*} \dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }=\det \left( \begin{array}{cc} \cos \theta & -r\ \text{sen}\ \theta \\ \ \text{sen}\ \theta & r\cos \theta \end{array} \right) =r\cos ^{2}\theta +r\ \text{sen}\ ^{2}\theta =r. \end{equation*} Entonces \begin{eqnarray*} \iint_{D}xy^{2}\,dx\,dy &=&\iint_{D_{1}}\left( f\circ L\right) \left( u,v\right) \left\vert \dfrac{\partial \left( x,y\right) }{ \partial \left( r,\theta \right) }\right\vert \,dr\,d\theta \\ &=&\int_{0}^{2}\int_{0}^{2\pi }\left( r\cos \theta +2\right) \left( r^{2}\ \text{sen}^{2}\theta \right) r\,d\theta \,dr \\ &=&\int_{0}^{2}\int_{0}^{2\pi }r^{4}\ \text{sen} ^{2}\theta \cos \theta +2r^{3}\ \text{sen} ^{2}\theta \,d\theta \,dr \\ &=&\int_{0}^{2}\left. \dfrac{r^{4}}{3}\ \text{sen} ^{3}\theta +2r^{3}\left( \dfrac{1 }{2}\theta -\dfrac{1}{2}\cos \theta\ \text{sen}\ \theta \right) \right\vert _{0}^{2\pi }dr \\ &=&\int_{0}^{2}2\pi r^{3}dr \\ &=&\left. \dfrac{2\pi r^{4}}{4}\right\vert _{0}^{2} \\ &=&8\pi \end{eqnarray*}
Solución:
Vamos a dibujar las gráficas cartesianas de la funciones \(r=2\) y \( r=2+2\cos \theta ,\) por ello utilizaremos, como dijimos antes, el plano cartesiano \(\Theta R,\) o sea, en el eje horizontal marcaremos los valores de \(\theta \) y en el vertical los de \(r.\)
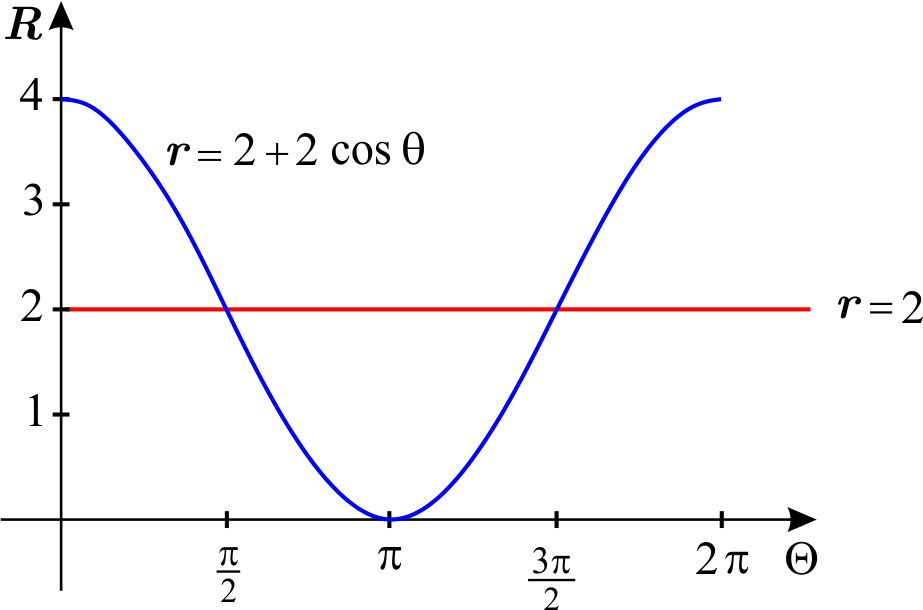
Ahora dibujamos sus gráficas polares en el plano \(XY\) y sombreamos la región \(D \). Dichas gráficas son el círculo de radio 2 (Ver Coordenadas Polares - Círculos) y una cardioide (Ver Coordenadas Polares - Caracoles)., respectivamente.
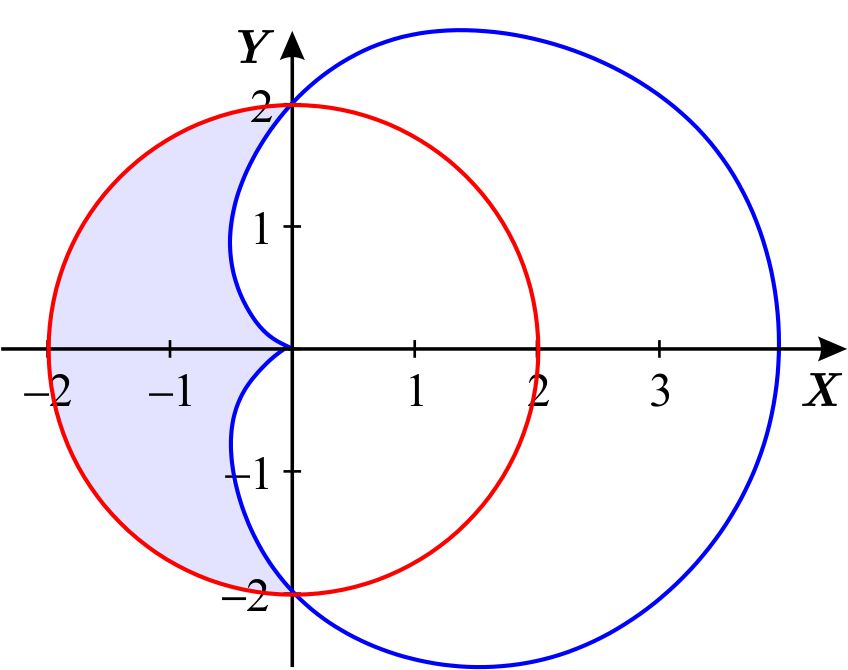
Observamos que dicha región \(D \) es la imagen bajo la transformación de coordenadas polares \(T_{p} \) de la región \(D_{1}\) que aparece sombreada en la figura de abajo.
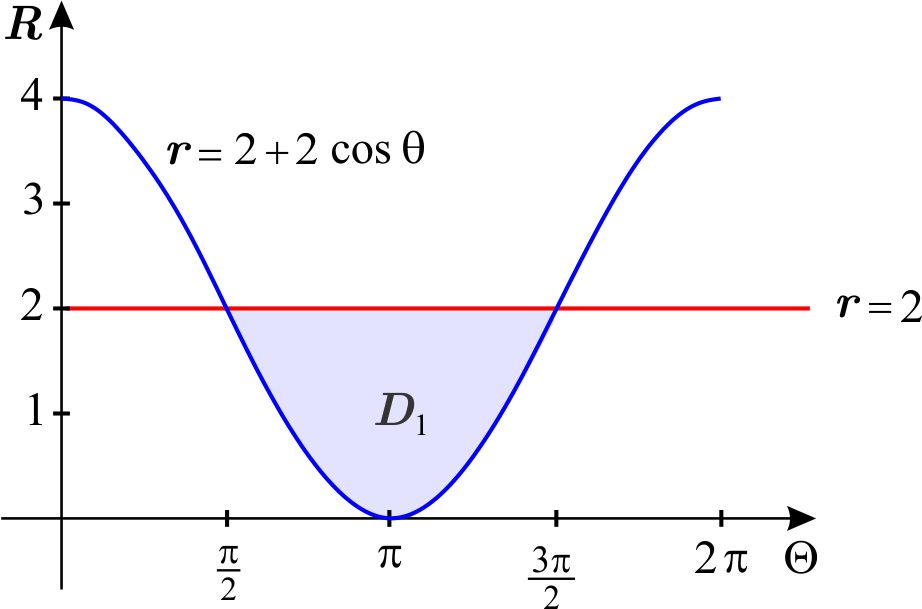
Esto queda indicado en la siguiente figura
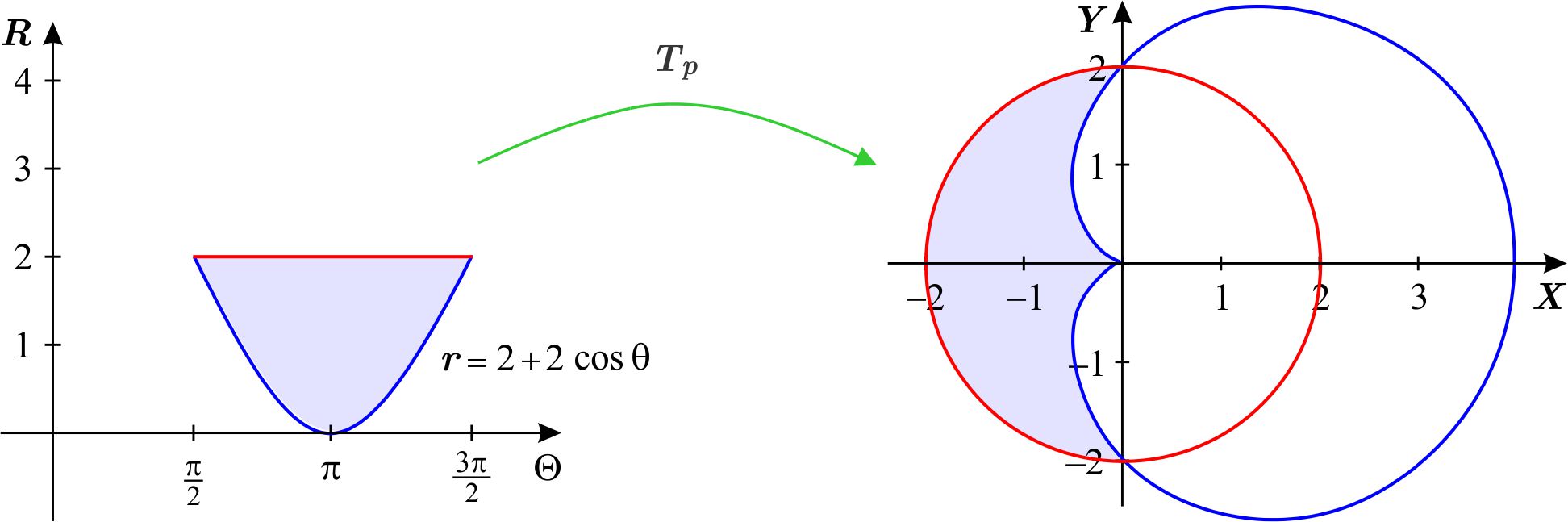
El área a calcular es la integral de la función \(f=1\) sobre \(D.\) Al aplicar el Teorema de cambio de variables obtenemos \begin{eqnarray*} \iint_{D}dx\,dy &=&\iint_{D_{1}}\left( f\circ T_{p}\right) \left( r,\theta \right) \left\vert \dfrac{\partial \left( x,y\right) }{\partial \left( r,\theta \right) }\right\vert \,dr\,d\theta \\ &=&\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}\int_{2+\cos \theta }^{2}r\,dr\,d\theta \\ &=&\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}\left. \dfrac{r^{2}}{2} \right\vert _{2+\cos \theta }^{2}d\theta \\ &=&\dfrac{1}{2}\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}4-\left( 2+\cos \theta \right) ^{2}\,d\theta \\ &=&\dfrac{1}{2}\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}4-\left( 4+4\cos \theta +\cos ^{2}\theta \right) \,d\theta \\ &=&\dfrac{1}{2}\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}-4\cos \theta -\cos ^{2}\theta \,d\theta \\ &=&\dfrac{1}{2}\int_{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}}-4\cos \theta -\left( \dfrac{1+\cos 2\theta }{2}\right) \,d\theta \\ &=&\dfrac{1}{2}\left. -4\ \text{sen}\ \theta -\dfrac{\theta }{2}-\dfrac{ \ \text{sen}\ 2\theta }{4}\right\vert _{\tfrac{\pi }{2}}^{\tfrac{3\pi }{2}} \\ &=&\dfrac{1}{2}\left[ 4-\dfrac{3\pi }{4}-\left( -4-\dfrac{\pi }{4}\right) \right] \\ &=&\dfrac{1}{2}\left( 8-\dfrac{1}{2}\pi \right) \\ &=&4-\dfrac{\pi }{4}. \end{eqnarray*}
Solución:
En el plano cartesiano \(\Theta R\) dibujamos las gráficas de las curvas \( r=6\cos 2\theta \) y \(r=4\)
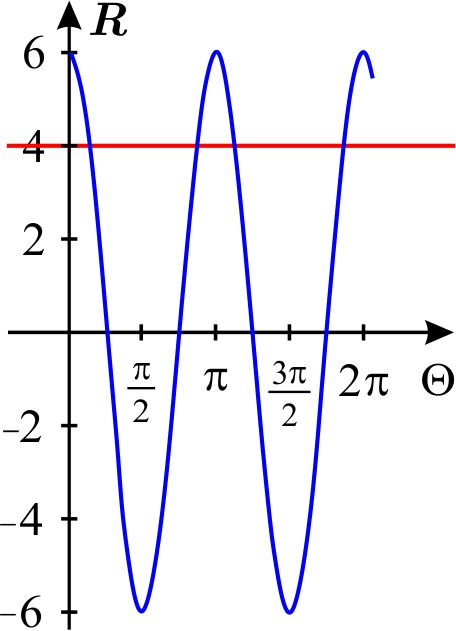
Sus gráficas polares son la rosa de 4 pétalos (Ver Coordenadas Polares - Rosas) y el círculo con centro en el origen y radio 4 (Ver Coordenadas Polares - Círculos) , respectivamente.
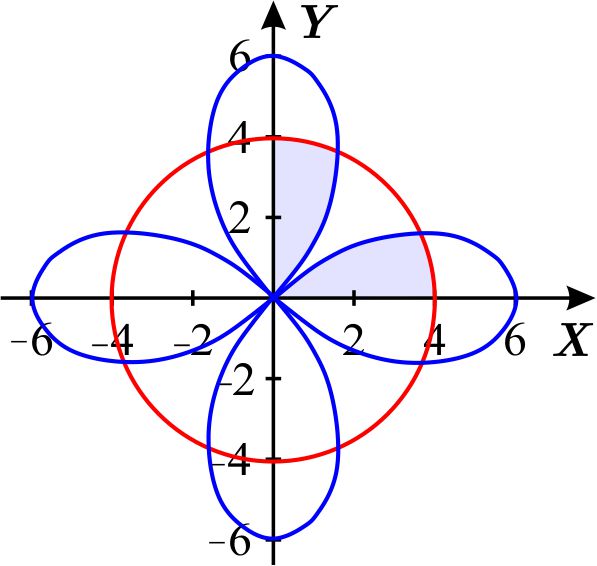
La región \(D\) cuya área se pidió determinar es la que está sombreada en la figura anterior.
La transformación de coordenadas polares \(T\) transforma las regiones sombreadas de la izquierda, en la figura siguiente, en \(D.\) La imagen bajo \( T \) de la región \(D_{1}\) sobre el intervalo \(\left[ 0,\dfrac{\pi }{4} \right] \) es la región sombreada dentro del pétalo horizontal, la que está en el pétalo vertical es la imagen bajo \(T\) de la región correspondiente al intervalo \(\left[ \dfrac{5\pi }{4},\dfrac{3\pi }{2} \right] .\)

Puesto que ambas regiones sombreadas dentro de la rosa tienen igual área, basta, para resolver nuestro ejemplo, calcular una de ellas y duplicar el resultado. Calcularemos la de la región \(D\) que está dentro del pétalo horizontal usando el teorema de cambio de variables. Así, \begin{equation*} A= \iint_{D}dx\,dy=\iint_{D_{1}}r\,dr\,d\theta . \end{equation*} Vamos a describir a \(D_{1} \) como una región de tipo 2. Para esto despejamos \(\theta \) en la ecuación \(r=6\cos \left( 2\theta \right) \): \begin{eqnarray*} r &=&6\cos \left( 2\theta \right) \\ \dfrac{r}{6} &=&\cos \left( 2\theta \right) \\ \arccos \dfrac{r}{6} &=&2\theta \\ \dfrac{1}{2}\arccos \dfrac{r}{6} &=&\theta . \end{eqnarray*} Por tanto, \begin{equation*} D_{1}=\left\{ \left( \theta ,r\right) \,\left\vert \,r\in \left[ 0,4\right] ,\quad \quad 0\leq \theta \leq \dfrac{1}{2}\arccos \dfrac{r}{6}\right. \right\} \end{equation*} y \begin{equation*} A=\int_{0}^{4}\int_{0}^{\tfrac{1}{2}\arccos \tfrac{r}{6}}r\,d\theta \,dr. \end{equation*} La integral que resulta después de calcular la integral con respecto a \( \theta ,\) no es fácil de determinar, por ello describimos la región en el plano cartesiano \(\Theta R\) como de tipo 1: \begin{eqnarray*} 6\cos \left( 2\theta \right) &=&4 \\ \cos \left( 2\theta \right) &=&\dfrac{2}{3} \\ 2\theta &=&\arccos \dfrac{2}{3} \\ \theta &=&\dfrac{1}{2}\arccos \left( \dfrac{2}{3}\right) . \end{eqnarray*}
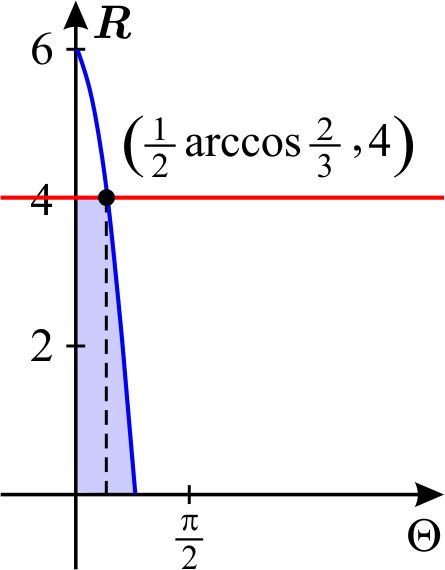
\begin{equation*} \int_{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}}\int_{0}^{4}r\,dr\,d\theta +\int_{ \tfrac{1}{2}\arccos \tfrac{2}{3}}^{\tfrac{\pi }{4}}\int_{0}^{6\cos 2\theta }r\,dr\,d\theta \end{equation*} Calculamos la primera integral \begin{eqnarray*} \int_{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}}\int_{0}^{4}r\,dr\,d\theta &=&\int_{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}}\left. \dfrac{r^{2}}{2} \right\vert _{0}^{4}d\theta \\ &=&\int_{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}}8\,d\theta \\ &=&\left. 8\theta \right\vert _{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}} \\ &=&8\left( \frac{1}{2}\arccos \dfrac{2}{3}\right) \\ &=&4\arccos \left( \dfrac{2}{3}\right) \end{eqnarray*} y la segunda integral es \begin{eqnarray*} \int_{\tfrac{1}{2}\arccos \tfrac{2}{3}}^{\tfrac{\pi }{4}}\int_{0}^{6\cos 2\theta }r\,dr\,d\theta &=&\int_{\tfrac{1}{2}\arccos \tfrac{2}{3}}^{\tfrac{ \pi }{4}}\left. \dfrac{r^{2}}{2}\right\vert _{0}^{6\cos 2\theta }d\theta \\ &=&\int_{\tfrac{1}{2}\arccos \tfrac{2}{3}}^{\tfrac{\pi }{4}}18\cos 2\theta \,d\theta \\ &=&\left. 9\left( -\ \text{sen}\ 2\theta \right) \right\vert _{\tfrac{1}{2} \arccos \tfrac{2}{3}}^{\tfrac{\pi }{4}} \\ &=&-9+9\ \text{sen}\ 2\left( \frac{1}{2}\arccos \frac{2}{3}\right) \\ &=&-9+9\ \text{sen}\ \left( \arccos \frac{2}{3}\right) \end{eqnarray*} así \begin{equation*} \int_{0}^{\tfrac{1}{2}\arccos \tfrac{2}{3}}\int_{0}^{4}r\,dr\,d\theta +\int_{ \tfrac{1}{2}\arccos \tfrac{2}{3}}^{\tfrac{\pi }{4}}\int_{0}^{6\cos 2\theta }r\,dr\,d\theta =4\arccos \left( \dfrac{2}{3}\right) -9+9\ \text{sen}\ \left( \arccos \frac{2}{3}\right) \approx 1.072 \end{equation*} Por consiguiente, el área buscada es el doble de la anterior: \begin{equation*} 2\left( 4\arccos \left( \dfrac{2}{3}\right) -9+9\ \text{sen}\ \left( \arccos \frac{2}{3}\right) \right) \approx 2\times 1.072=2.144 \end{equation*}