 |
Coordenadas Polares
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos
Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)
\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM
|  |
|
Rosas
Las rosas son curvas con forma de flor. En el
Ejemplo 3
de la sección de Gráficas en Coordenadas Polares,
dibujamos una de ellas. Las gráficas polares de las
ecuaciones de las formas:
\begin{eqnarray*}
r & = & a \ \text{sen} \ \left( n\theta \right) \\
r & = & a\cos \left( n\theta \right)
\end{eqnarray*}
con \(n\in \mathbb{Z}\) y \(a\in \mathbb{R}\), son llamadas rosas. El
largo de cada uno de los pétalos es \(\left\vert a\right\vert .\)
Analizamos primero la curva \(r=a\cos \left( n\theta \right) .\)
En este caso, la gráfica polar correspondiente es siempre simétrica
con respecto al eje \(X\), ya que
\begin{equation*}
a\cos \left( n\left( -\theta \right) \right) =a\cos \left( n\theta \right)
=r.
\end{equation*}
Por el Primer criterio de simetría basta considerar valores de \(\theta \) no
negativos para obtener la gráfica correspondiente.
- Veamos el caso en el que \(n\) es impar.
La función de \(\theta ,\) \(r=a\cos \left( n\theta \right) \) es periódica,
de periodo \(2\pi \). Entonces basta, en principio, considerar la gráfica
cartesiana de la función en un intervalo de longitud \(2\pi \), pues
para ángulos fuera de éste los valores de \(\cos \left( n\theta \right) \) y por
tanto, de \(r\) se repiten.
Sin embargo vemos algo más: para cada valor \(\theta ^{\prime }\in \left[
\pi ,2\pi \right] ,\) tenemos que \(\theta ^{\prime }=\theta +\pi \) para algún
\(\theta \in \left[ 0,\pi \right] \) (tómese \(\theta =\theta
^{\prime }-\pi \)) y
\begin{eqnarray*}
r^{\prime } & = & \cos \theta ^{\prime }=\cos \left( n\left( \theta +\pi
\right) \right) \\
& = & \cos \left( n\theta \right) \cos \left( n\pi \right) \\
& = & -\cos \left( n\theta \right) ,\quad \text{ya que }n\text{ es impar} \\
& = & -r.
\end{eqnarray*}
Así que \(\left( r^{\prime },\theta ^{\prime }\right) =\left( -r,\theta
+\pi \right) \) y éstas son otras coordenadas polares del punto
correspondiente a \(\left( r,\theta \right) ,\) por lo que \(\left( r^{\prime
},\theta ^{\prime }\right) \) determina el mismo punto en el plano polar que
la pareja \(\left( r,\theta \right) \). De manera que para trazar la gráfica
polar nos bastará considerar el intervalo \(\left[ 0,\pi \right] ,\)
pues, por lo recién dicho, los puntos que se obtienen en la gráfica
polar al considerar valores de \(\theta \) en el intervalo \(\left[ \pi ,2\pi
\right] \) serán puntos previamente obtenidos para \(\theta \) en el
intervalo \(\left[ 0,\pi \right] .\)
En el intervalo \(\left[ 0,\pi \right] \) consideremos los intervalos
consecutivos \[\left[ 0,\dfrac{\pi }{2n}\right], \left[ \dfrac{\left(
2m-1\right) \pi }{2n},\dfrac{\left( 2m+1\right) \pi }{2n}\right] \] para \(
1\leq m\leq n-1\) y \[\left[ \dfrac{\left( 2n-1\right) \pi }{2n},\pi \right] \]
En el plano \(\Theta R\) la porción de la gráfica obtenida entre dos
puntos consecutivos en los que la función vale cero determinará un pétalo de la rosa en el plano polar. Entonces al graficar la porción
correspondiente a cada uno de los intervalos \(\left[ \dfrac{\pi }{2n},\dfrac{
\left( 2n-1\right) \pi }{2n}\right] \) obtenemos \(n-1\) pétalos.
Asimismo, la porción de la gráfica correspondiente a los intervalos \(\left[ 0,
\dfrac{\pi }{2n}\right] \) y \(\left[ \left( \dfrac{2n-1}{2n}\right) \pi ,\pi
\right] \) determinan un pétalo más, luego, la gráfica polar de \(
r=a\cos \left( n\theta \right) \) con \(n\) impar tiene \(n\) pétalos.
En resumen, si \(n\) es impar, la rosa tiene \(n\) pétalos, si por el
contrario, \(n\) es par, tendrá \(2n\) pétalos. Justificaremos este
hecho más adelante.
Ejemplos
- Dibuja la gráfica de \(r=3\cos \left( 5\theta \right) .\)
Solución:
Dibujamos la gráfica cartesiana en \(\Theta R\) de \(r=3\cos \left( 5\theta
\right) \) en \(\left[ 0,\pi \right] .\)
Analizando en el intervalo \(\left[ 0,\dfrac{2\pi }{10}\right] =\left[ 0,
\dfrac{\pi }{5}\right] \) y dibujando ya en el plano polar tenemos:
La gráfica completa es:
- Dibuja la gráfica de \(r=a\cos \left( 3\theta \right) ,\) con \(a < 0.\)
Solución:
Como sabemos, la gráfica es simétrica con respecto al eje \(X\) y
esperamos que tenga tres pétalos. Dibujamos en el plano \(\Theta R\) la gráfica
cartesiana de \(r=\cos \left( 3\theta \right) \) en \(\left[ 0,\pi
\right] .\)
entonces, en el mismo plano, \(r=a\cos \left( 3\theta \right) \) con \(a < 0,\)
tiene por gráfica:
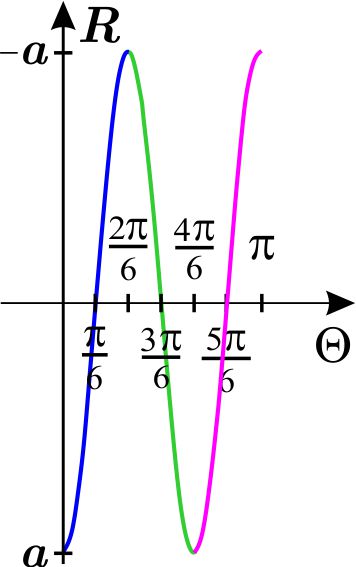
Analizando en el intervalo \(\left[ 0,\dfrac{2\pi }{6}\right] =\left[ 0,
\dfrac{\pi }{3}\right] \) y dibujando en el plano polar tenemos:
Analizando en \(\left[ \dfrac{2\pi }{6},\dfrac{4\pi }{6}\right] =\left[
\dfrac{\pi }{3},\dfrac{2\pi }{3}\right] ,\) que corresponde a la parte verde,
y en \(\left[ \dfrac{4\pi }{6},\pi \right] =\left[ \dfrac{2\pi }{3},\pi
\right] ,\) que corresponde a la rosa, obtenemos
- Veamos ahora el caso en el que \(n\) es par.
En este caso la curva es simétrica con respecto al eje \(Y,\) ya que
\begin{eqnarray*}
a\cos \left( n\left( \pi -\theta \right) \right) & = & a\cos \left( n\pi
-n\theta \right) \\
& = & a\left( \cos \left( n\pi \right) \cos \left( n\theta \right) +
\text{sen} \ \left( n\pi \right) \ \text{sen} \ \left( n\theta \right) \right) \\
& = & a\cos \left( n\pi \right) \cos \left( n\theta \right) \\
& = & a\cos \left( n\theta \right) \quad \text{ya que }n\text{ es par} \\
& = & r.
\end{eqnarray*}
La función de \(\theta ,\) \(r=a\cos \left( n\theta \right) \) es periódica,
de periodo \(2\pi \). Basta considerar la gráfica cartesiana de la
función en un intervalo de longitud \(2\pi \), pues para valores fuera de
éste los de \(\cos \left( n\theta \right) \) y por tanto, de \(r\) se
repiten.
Veamos ahora la gráfica cartesiana de \(r=a\cos n\theta ,\) \(n\) par, \(a>0,\)
en el intervalo \(\left[ 0,2\pi \right] .\)
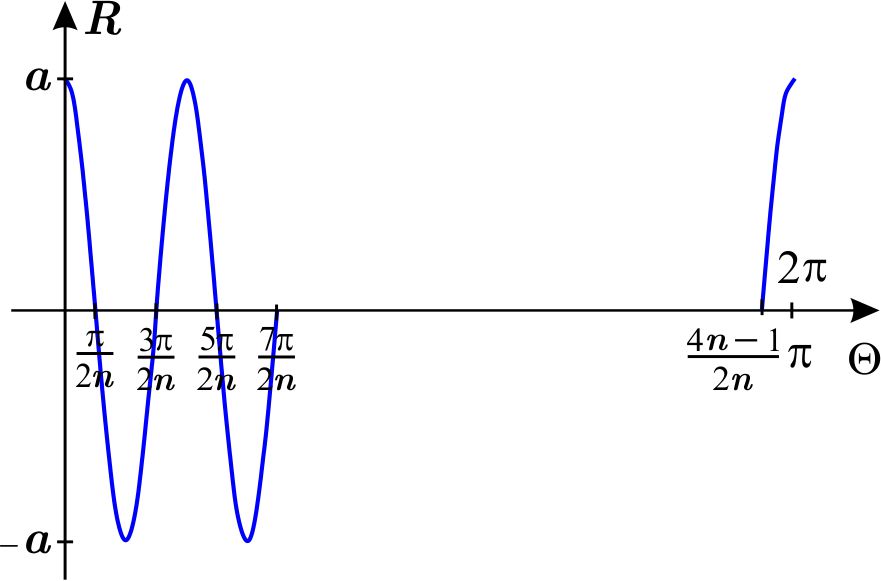
Por cada intervalo \(\left[ \dfrac{\left( 2k+1\right) \pi }{2n},\dfrac{\left(
2k+3\right) \pi }{2n}\right] ,0\leq k\leq 2\left( n-1\right) ,k\in \mathbb{Z}\) se
determina un pétalo completo en la gráfica polar de la función,
es decir, hay \(2n-1\) pétalos completos. Pero faltan los intervalos \(
\left[ 0,\dfrac{\pi }{2n}\right] \) y \(\left[ \left( \dfrac{4n-1}{2n}\right)
\pi ,2\pi \right] \) los cuales determinan un pétalo más, luego, las
rosas de la forma \(r=a\cos \left( n\theta \right) \), con \(n\) par, tienen \(2n\)
pétalos.
Ejemplos
- Dibujar la gráfica de \(r=3\cos \left( 2\theta \right) .\)
Solución:
Dibujamos primero la gráfica cartesiana en el plano \(R\Theta \) de \(
r=3\cos \left( 2\theta \right) \) en el intervalo \(\left[ 0,2\pi \right] \).
La gráfica polar es
Un análisis similar al que hemos hecho, puede hacerse para el caso \(r=a
\ \text{sen} \ \left( n\theta \right) .\)
Si \(n=1\) se trata de un círculo, el cual puede ser considerado como una
rosa de un sólo pétalo.
Para las ecuaciones de la forma \(r=a \ \text{sen} \ \left( n\theta \right) \)
tenemos que al sustituir \(\left( r,\theta \right) \) por \(\left( -r,-\theta
\right) \) obtenemos:
\begin{eqnarray*}
-r & = & a \ \text{sen} \ \left( n\left( -\theta \right) \right) \\
& = & -a \ \text{sen} \ \left( n\theta \right) .
\end{eqnarray*}
Es decir, la gráfica es simétrica respecto al eje \(Y.\) Sin importar
si \(n\) es par o impar.
Ejemplo
- Dibujar la gráfica de \(r=2 \ \text{sen} \ \left( 4\theta \right) .\)
Solución:
Dibujamos primero la gráfica cartesiana en el plano \(R\Theta \) de \(r=2
\ \text{sen} \ \left( 4\theta \right) \) en el intervalo \(\left[ 0,2\pi \right]
\).
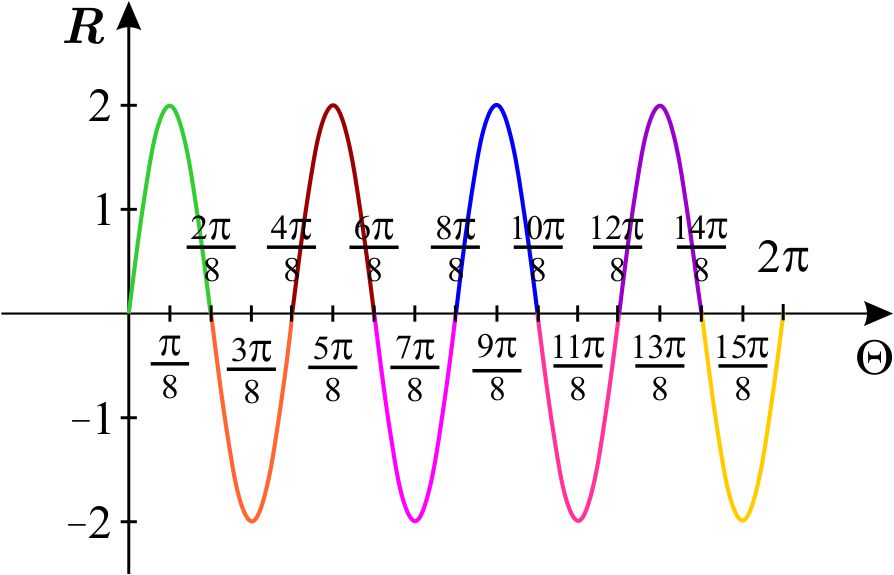La gráfica polar es
Ejercicios
- \(r=5 \ \text{sen} \ \left( 3\theta \right) .\)
- \(r=\dfrac{4}{5}\cos \left( 2\theta \right) .\)
- \(r= \ \text{sen} \ \left( 2\theta \right) .\)
- \(r=2\cos \left( 5\theta \right) .\)
Universidad Nacional Autónoma de México