Coordenadas Polares

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza$^2$, Carlos Hernández Garciadiego$^1$, Emma Lam Osnaya$^2$

$^1$ Instituto de Matemáticas, UNAM; $^2$ Facultad de Ciencias, UNAM

Caracoles

Los caracoles son curvas que como su nombre lo indica, tienen forma de caracol. Las gráficas polares de las ecuaciones de las formas \begin{eqnarray*} r &=&a+b\ \text{sen}\ \theta \\ r &=&a+b\cos \theta \end{eqnarray*} con $a,b\in \mathbb{R}$ son caracoles.

Dibujar la gráfica de $r=a+b\ \text{sen}\ \theta $ con $a,b>0.$
Solución:
El primer criterio de simetría no funciona.
Por otra parte, sustituyendo $\theta $ por $\pi -\theta ,$ se tiene: \begin{eqnarray*} r &=&a+b\ \text{sen}\left( \pi -\theta \right) \\ &=&a+b\left( \text{sen}\ \pi \cos \theta -\cos \pi\ \text{sen}\ \theta \right) \\ &=&a+b\ \text{sen}\ \theta , \end{eqnarray*} por lo que la gráfica es simétrica con respecto al eje $Y.$
Los dos criterios restantes tampoco se cumplen en este caso.
Para dibujar la gráfica polar, tracemos primero la gráfica cartesiana de $r=b\ \text{sen}\ \theta $ en el intervalo $\left[ 0,2\pi \right] $

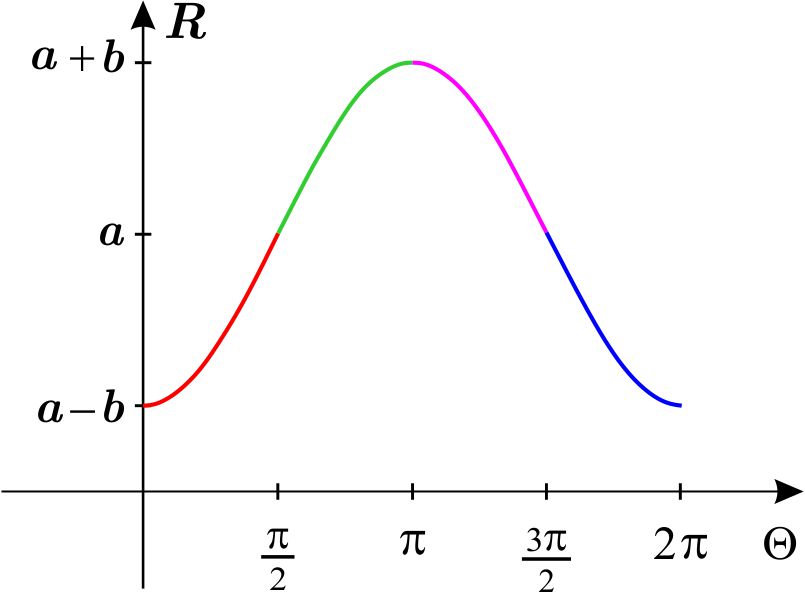
Ahora dibujamos la gráfica cartesiana de $r=a+b\ \text{sen}\ \theta $ en el intervalo $\left[ 0,2\pi \right] .$
Debemos considerar tres casos:
- Si $a=b$
- Si $a < b$
- Si $a > b$
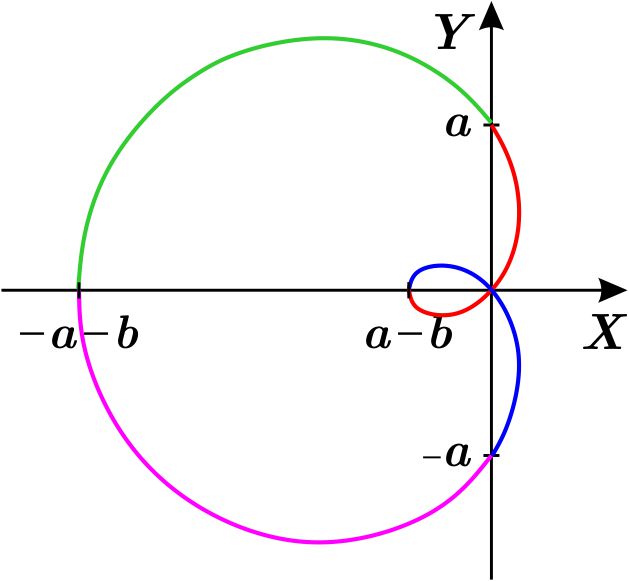
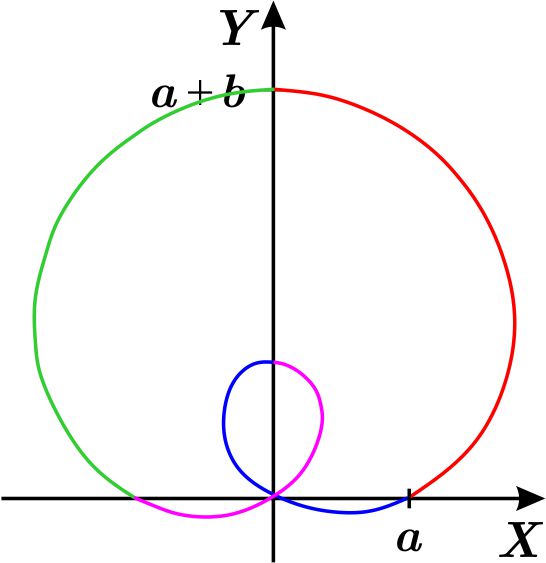
Entonces la gráfica polar puede ser alguna de las tres siguientes, de acuerdo como se comparen los reales $a$ y $b$:
- Si $a=b$
  
  Observación: En este caso en que $a=b$ la curva tiene apariencia de un corazón, por esta razón, a dichos caracoles se les llama cardioides.
- Si $a < b$
- Si $a > b$
Recuerda que basta analizar, por ejemplo, en los intervalos $\left[ 0,\dfrac{ \pi }{2}\right] $ y $\left[ \pi ,\dfrac{3\pi }{2}\right] $ y reflejar con respecto al eje $Y$ lo obtenido.
Dibujar la gráfica de $r=a-b\cos \theta $, con $a,$ $b>0.$
Solución:
Si sustituimos $\theta $ por $-\theta ,$ obtenemos \begin{eqnarray*} r &=&a-b\cos \left( -\theta \right) \\ &=&a-b\cos \theta \end{eqnarray*} por lo que la gráfica es simétrica con respecto al eje $X.$ Por el Primer criterio de simetría basta considerar valores de $\theta $ no negativos para obtener la gráfica correspondiente.
Los dos criterios restantes no se cumplen en este caso.
Para dibujar la gráfica polar, tracemos primero la gráfica cartesiana de $r=-b\cos \theta $ en el intervalo $\left[ 0,2\pi \right] .$

Debemos considerar tres casos:
- Si $a=b$
- Si $a < b$
- Si $a>b$
Entonces la gráfica polar puede ser alguna de las tres siguientes, de acuerdo como se comparen los reales $a$ y $b$:
- Si $a=b$
- Si $a < b$
- Si $a > b$