Coordenadas Polares Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Gráficas en coordenadas polares

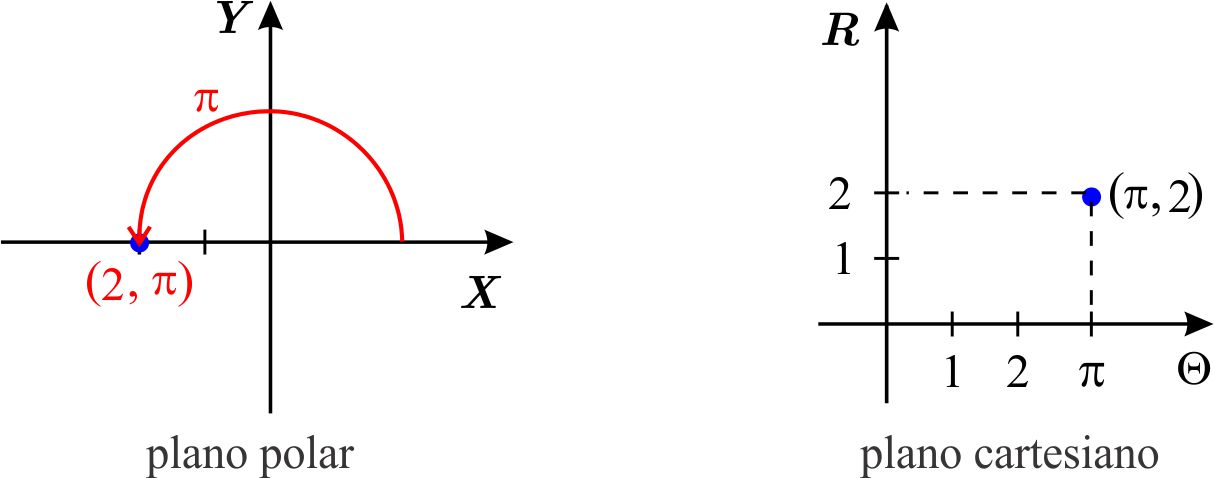
Observen que en el plano cartesiano de la derecha hemos llamado al eje horizontal \(\Theta\) y al vertical \(R\). Esto lo hacemos porque en lo que sigue graficaremos en este plano funciones del tipo \(r=f\left( \theta \right) \) y es costumbre que los valores de la variable independiente se tomen en el eje horizontal.

Deseamos ahora trazar las gráficas de curvas definidas en términos de ecuaciones en coordenadas polares del tipo \(F\left( r,\theta \right) =0,\) donde \(F\) es una función real de dos variables. Así, debemos localizar en el plano polar cada punto tal que algunas de sus coordenadas polares \(\left( r,\theta \right) \) satisfacen dicha ecuación.

Observación. Noten que en el párrafo anterior dijimos algunas de sus coordenadas polares. Por ejemplo, consideremos la función \(F\left( r,\theta \right) =\theta -\pi .\) El punto con coordenadas polares principales \(\left( 1,0\right) \) está en la gráfica de \(F\left( r,\theta \right) =\theta -\pi =0\), ya que no obstante que la pareja \(\left( 1,0\right) \) no satisface esa ecuación, sus coordenadas polares equivalentes \(\left( -1,\pi \right) \) si lo hacen.

Una manera de trazar las gráficas de curvas definidas por ecuaciones polares \(F\left( r,\theta \right) =0\) es localizar en el plano polar algunos puntos \((r,\theta )\) que la satisfagan, uniéndolos posteriormente de acuerdo con la información que proporciona la gráfica de la curva en el plano cartesiano \(\Theta R\). Ilustramos este procedimiento en el siguiente:

Ejemplo

1. Dibujar la gráfica polar de la curva \(r=\ \text{sen}\ \theta \).

   Solución:

   Consideramos la ecuación \(r=\ \text{sen}\ \theta \). Damos valores a \( \theta \) para determinar algunas soluciones \((r,\theta )\) de dicha ecuación \begin{equation*} \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \theta & 0 & \dfrac{\pi }{6} & \dfrac{\pi }{3} & \dfrac{\pi }{2} & \dfrac{2\pi }{3} & \dfrac{5\pi }{6} & \pi & \dfrac{7\pi }{6} & \dfrac{5\pi }{4} & \dfrac{4\pi }{3} & \dfrac{3\pi }{2} & \dfrac{5\pi }{3} & \dfrac{11\pi }{6} \\ \hline r & 0 & \dfrac{1}{2} & \dfrac{\sqrt{3}}{2} & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{1}{2} & 0 & -\dfrac{1}{2} & -\dfrac{1}{\sqrt{2}} & - \dfrac{\sqrt{3}}{2} & -1 & -\dfrac{\sqrt{3}}{2} & -\dfrac{1}{2} \\ \hline \end{array} \end{equation*} dibujamos estos puntos en el plano polar:

   

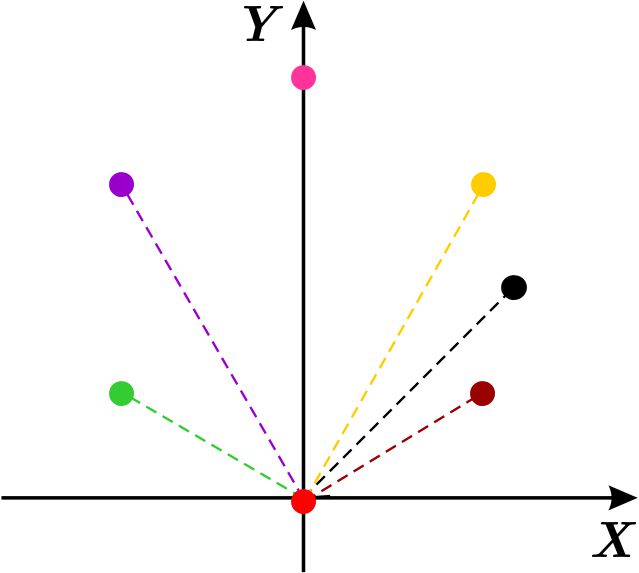
   Ahora falta unir los puntos. Para ello consideremos la gráfica cartesiana de la función \(f\left( \theta \right) =\ \text{sen}\ \theta \) en el plano cartesiano \(\Theta R\):

   

   Observemos que si \(\theta \) varía de \(0\) a \(\dfrac{\pi }{2}\), \(r\) crece de \(0\) a \(1\) y si \(\theta \) varía de \(\dfrac{\pi }{2}\) a \(\pi \), \( r\) decrece de \(1\) a \(0.\)

   No es necesario analizar valores para \(\theta \) fuera del intervalo \(\left[ 0,\pi \right] ,\) los puntos, en el plano polar, que se obtienen, son los mismos que se obtuvieron en ese intervalo. Por ejemplo, si \(\pi \leq \theta \leq 2\pi \), entonces \( \text{sen}\ \theta =-\ \text{sen}\ \left( \theta -\pi \right) \) y por tanto, \(\left( \ \text{sen}\ \theta ,\theta \right) \) y \( \left( \ \text{sen}\ \left( \theta -\pi \right) ,\theta -\pi \right) \) son coordenadas polares del mismo punto y \(0\leq \theta -\pi \leq \pi \).

   

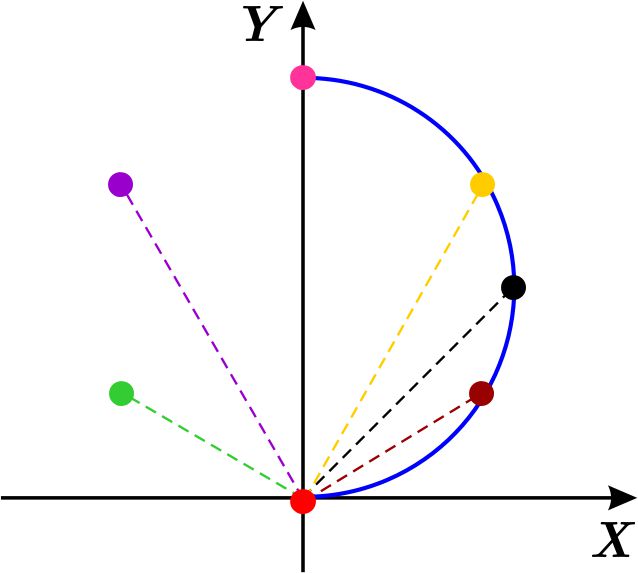
   Con este análisis tenemos la impresión de que los puntos se encuentran sobre un círculo. Esto es cierto, podemos convencernos obteniendo la ecuación cartesiana correspondiente: \begin{eqnarray*} r & = & \ \text{sen}\ \theta \\ r^{2} & = & r\ \text{sen}\ \theta \\ x^{2}+y^{2} & = & y \\ x^{2}+y^{2}-y & = & 0 \\ x^{2}+\left( y-\dfrac{1}{2}\right) ^{2} & = & \dfrac{1}{4} \end{eqnarray*} que es la ecuación cartesiana del círculo de radio \(\dfrac{1}{2}\) con centro en el punto \(\left( 0,\dfrac{1}{2}\right) .\)

   Es importante observar en el plano cartesiano \(\Theta R\) cómo cambian los valores de \(r\) a medida que \(\theta \) varía. Podemos así obtener una gráfica en el plano polar sin necesidad de usar una tabla como la que aparece al inicio de este ejemplo.

   
2. Dibujar la gráfica de la curva con ecuación polar \(r=2+2\cos \theta .\)

   Solución:

   Dibujamos la gráfica cartesiana de la función \(r=2+2\cos \theta \) en el intervalo \(\left[ 0,2\pi \right] \)

   

   Hacemos una tabla conteniendo datos acerca del comportamiento de la función en el plano cartesiano \(\Theta R.\) \begin{equation*} \begin{array}{|r|c|c|c|c|} \hline \theta \text{ en} & \left[ 0,\dfrac{\pi }{2}\right] & \left[ \dfrac{\pi }{2} ,\pi \right] & \left[ \pi ,\dfrac{3\pi }{2}\right] & \left[ \dfrac{3\pi }{2},2\pi \right] \\ \hline r & 4\searrow 2 & 2\searrow 0 & 0\nearrow 2 & 2\nearrow 4 \\ \hline \end{array} \end{equation*} Analizamos cuando \(\theta \) varía de \(0\) a \(\dfrac{\pi }{2}\):

   

   Continuando de la misma manera, podemos dibujar en el plano polar toda la gráfica de \(r=2+2\cos \theta \), llamada cardioide

   
3. Trazar la curva con ecuación polar \(r=\cos 2\theta .\)

   Solución:

   Dibujamos la gráfica cartesiana de la función \(r=\cos 2\theta \) en el intervalo \(\left[ 0,2\pi \right] \)

   

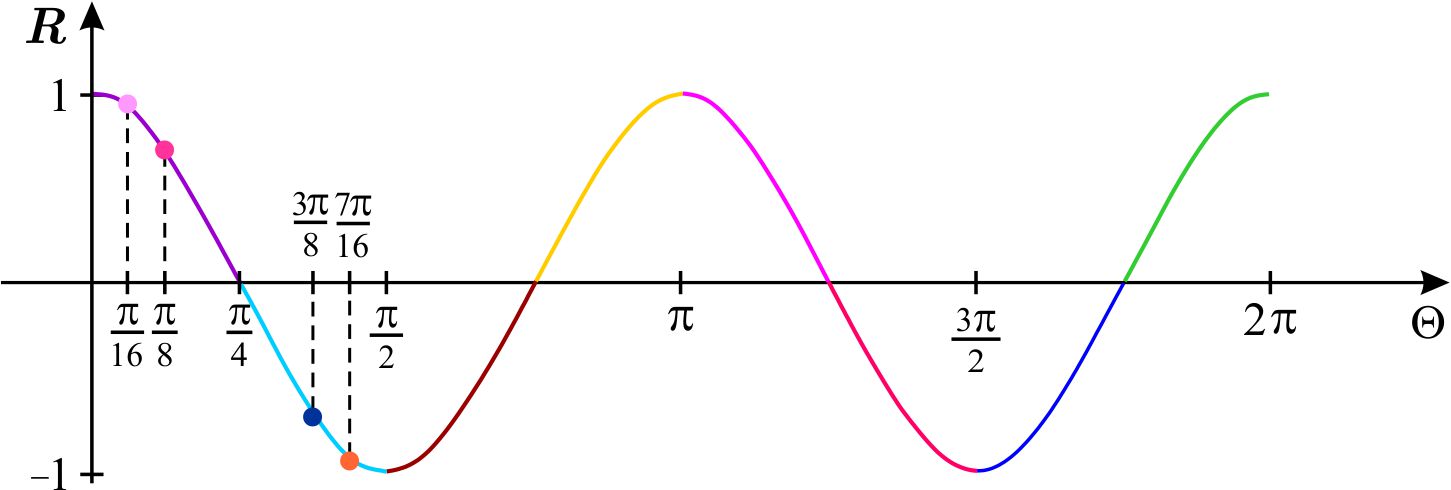
   Hacemos una tabla conteniendo datos acerca del comportamiento de la función en el plano \(\Theta R\) \begin{equation*} \begin{array}{|r|l|l|l|l|l|l|l|l|} \hline \theta \text{ en} & \left[ 0,\dfrac{\pi }{4}\right] & \left[ \dfrac{\pi }{4},\dfrac{\pi }{2}\right] & \left[ \dfrac{\pi }{2},\dfrac{3\pi }{4} \right] & \left[ \dfrac{3\pi }{4},\pi \right] & \left[ \pi ,\dfrac{ 5\pi }{4}\right] & \left[ \dfrac{5\pi }{4},\dfrac{3\pi }{2}\right] & \left[ \dfrac{3\pi }{2},\dfrac{7\pi }{4}\right] & \left[ \dfrac{7\pi }{4} ,2\pi \right] \\ \hline r & 1\searrow 0 & 0\searrow -1 & -1\nearrow 0 & 0\nearrow 1 & 1\searrow 0 & 0\searrow -1 & -1\nearrow 0 & 0\nearrow 1 \\ \hline \end{array} \end{equation*}

   Analizamos cuando \(\theta \) varía de \(0\) a \(\dfrac{\pi }{4}\) y de \( \dfrac{\pi }{4}\) a \(\dfrac{\pi }{2}\):

   

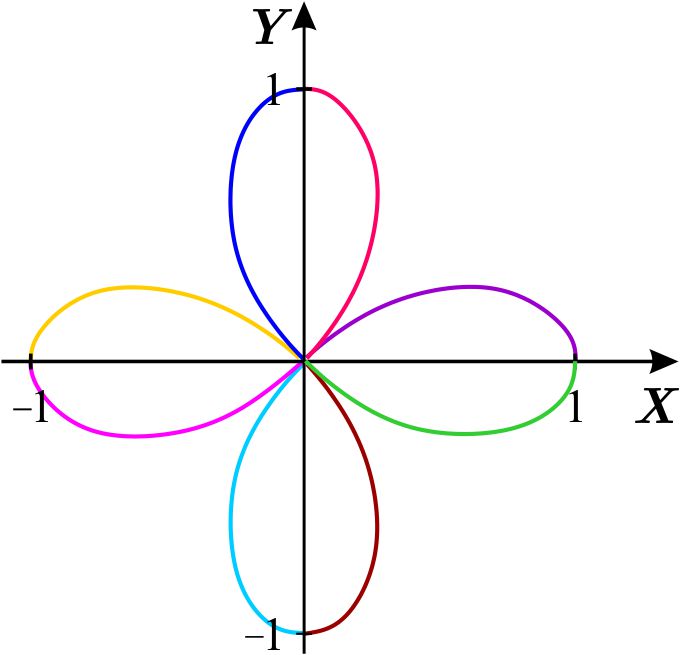
   Continuando de la misma manera, podemos dibujar en el plano \(XY\) toda la gráfica de \(r=\cos 2\theta \) llamada rosa de 4 pétalos.

   
4. Probar que el punto de coordenadas polares \(\left( 1,\dfrac{3\pi }{4} \right) \) está sobre la curva con ecuación polar \(r=\ \text{sen}\ 2\theta \).

   Solución:

   Para \(\theta =\dfrac{3\pi }{4},\) tenemos \begin{equation*} \ \text{sen}\ 2\theta =\ \text{sen}\ 2\left( \dfrac{3\pi }{4}\right) =\text{ sen}\dfrac{3\pi }{2}=-1\neq 1, \end{equation*}

   por lo que aparentemente el punto \(P\left( 1,\dfrac{3\pi }{4}\right) \) no está sobre la curva, pero sí lo está, ya que hay otras coordenadas polares del punto que sí satisfacen la ecuación, por ejemplo \begin{equation*} \left( -1,-\dfrac{\pi }{4}\right) , \end{equation*} son otras coordenadas polares de \(P\) y si sustituimos estos valores en la ecuación \(r=\ \text{sen}\ 2\theta ,\) obtenemos la igualdad verdadera: \begin{equation*} -1=\ \text{sen}\ 2\left( -\dfrac{\pi }{4}\right) =-\ \text{sen}\ \dfrac{\pi }{2 }. \end{equation*} Así, la ecuación se satisface. Por lo tanto, el punto \(\left( 1, \dfrac{3\pi }{4}\right) \) sí está sobre la curva. Este hecho se debe a que la representación polar \(\left( r,\theta \right) \) de cada punto no es única.

   Más adelante comentaremos algunos criterios que nos llevarán a trazar las gráficas de manera más sencilla.

Ejercicios

Encuentra en cada caso, la ecuación en coordenadas polares

1. \(x=3.\)

2. \(y=-1.\)

3. \(x-y=0.\)

4. \(5x-2y=0.\)

5. \(4x+4y=8.\)

6. \(xy=2.\)

7. \(y=\sqrt{x}.\)

8. \(y=3x^{2}.\)

9. \(x^{2}+y^{2}=9.\)

10. \(x^{2}+y^{2}-2x=0.\)

11. \(x^{2}+y^{2}-4x+6y=0.\)

12. \(y^{2}-2y-2x+11=0.\)

13. \(5x^{2}+4y^{2}=20.\)

14. \(2x^{2}-3y^{2}-6=0.\)

15. \(x^{2}+y^{2}-4x+4y+4=0.\)

    Encuentra en cada caso la ecuación en coordenadas cartesianas

16. \(\theta =\dfrac{\pi }{6}.\)

17. \(r=\sqrt{2}.\)

18. \(r=\dfrac{3}{5\ \text{sen}\ \theta -\cos \theta }.\)

19. \(r=5\cos \theta .\)

20. \(r\ \text{sen}\ \theta =7.\)

21. \(r\cos \theta =-1.\)

22. \(r\cos \left( \theta +\dfrac{\pi }{6}\right) =3.\)

23. \(r^{2}\cos \left( 2\theta \right) =2.\)

24. \(r^{2}\ \text{sen}\ \left( 2\theta \right) =4.\)

25. \(r^{2}=\ \text{sen}\ \left( 2\theta \right) .\)

26. \(r^{2}=\cos \left( 2\theta \right) .\)

27. \(r=3\cos \left( 3\theta \right) .\)

28. \(r=1-2\cos \theta .\)

29. \(r=3\csc \theta \cot \theta .\)

30. \(r=a\ \text{sen}\ \left( 3\theta \right) .\)

31. \(r\ \text{sen}\ \theta =e^{r\cos \theta }.\)

32. \(r\ \text{sen}\ \theta =r\cos \theta .\)

33. \(r+\cos \theta =3\ \text{sen}\ \theta .\)

34. \(r=\ \text{sen}\ \theta +\cos \theta .\)

35. \(r=\dfrac{1}{\cos \theta -\ \text{sen}\ \theta }.\)

36. \(r=2\tan \theta \sec \theta .\)

    Prueba que el punto \(\left( r,\theta \right) \) está sobre la curva indicada.

37. \(\left( r,\theta \right) =\left( 4,\dfrac{\pi }{2}\right) ,\qquad r=4\cos \left( 2\theta \right) .\)

38. \(\left( r,\theta \right) =\left( \dfrac{3}{2},\dfrac{3\pi }{2}\right) ,\qquad r=-3\ \text{sen}\ \left( \dfrac{\theta }{3}\right) .\)

39. \(\left( r,\theta \right) =\left( -5,\dfrac{\pi }{2}\right) ,\qquad r=5\left( 1+\cos \theta \right) .\)

40. \(\left( r,\theta \right) =\left( \dfrac{-4}{\sqrt{2}},\dfrac{\pi }{2} \right) ,\qquad r=4\cos \left( \dfrac{\theta }{2}\right) .\)