Coordenadas Polares

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Criterios de simetría

Los criterios de simetría nos ayudarán a obtener la gráfica polar de una ecuación polar: \begin{equation*} F\left( r,\theta \right) =0 \end{equation*} donde $F\left( r,\theta \right) $ es una función con valores reales. Consideremos un punto de coordenadas polares $\left( r,\theta \right) ,$ entonces el punto $\left( r,-\theta \right) $ es su simétrico con respecto al eje $X.$

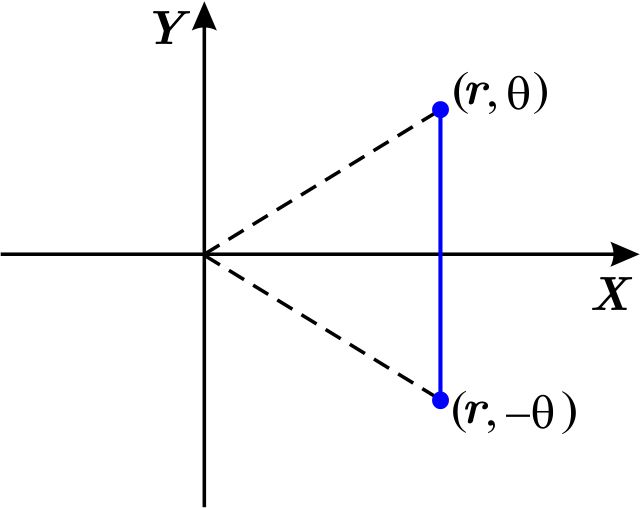
Así, la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al eje $X$ si se cumple que $F\left( r,-\theta \right) =0.$

Ahora, si tomamos el punto $\left( -r,\pi -\theta \right) ,$ ésta es otra representación del punto $\left( r,-\theta \right) $, es decir, también es el simétrico de $\left( r,\theta \right) $ respecto al eje $X.$

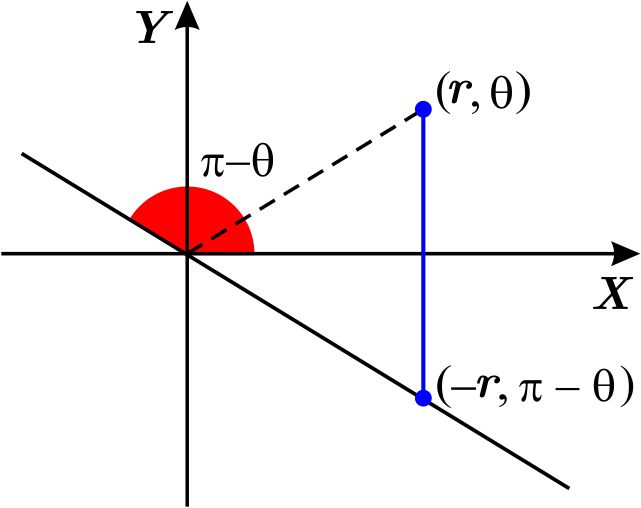
Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al eje $X$ si se cumple que $F\left( -r,\pi -\theta \right) =0.$

Observemos ahora que el punto $\left( r,\pi -\theta \right) $ es el simétrico de $\left( r,\theta \right) $ con respecto al eje $Y.$

Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al eje $Y$ si se cumple que $F\left( r,\pi -\theta \right) =0.$

Si tomamos ahora el punto $\left( -r,-\theta \right) ,$ éste también es simétrico al punto $\left( r,\theta \right) $ respecto al eje $Y$, por ser $\left( -r,-\theta \right) $ otra representación de $\left(r,\pi -\theta \right) .$

Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al eje $Y$ si se cumple que $F\left( -r,-\theta \right) =0.$

Inmediatamente vemos que el punto $\left( -r,\theta \right) $ es el simétrico de $\left( r,\theta \right) $ con respecto al origen, es decir, al trazar la recta que une $\left( r,\theta \right) $ con el origen, $\left( -r,\theta \right) $ se encuentra sobre ella a la misma distancia del origen que $\left( r,\theta \right) .$

Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al origen si se cumple que $F\left( -r,\theta \right) =0.$

Observamos que otra representación del punto $\left( -r,\theta \right) $ es $\left( r,\theta +\pi \right) ,$ es decir, $\left( r,\theta +\pi \right) $ es el simétrico del punto $\left( r,\theta \right) $ respecto al origen.

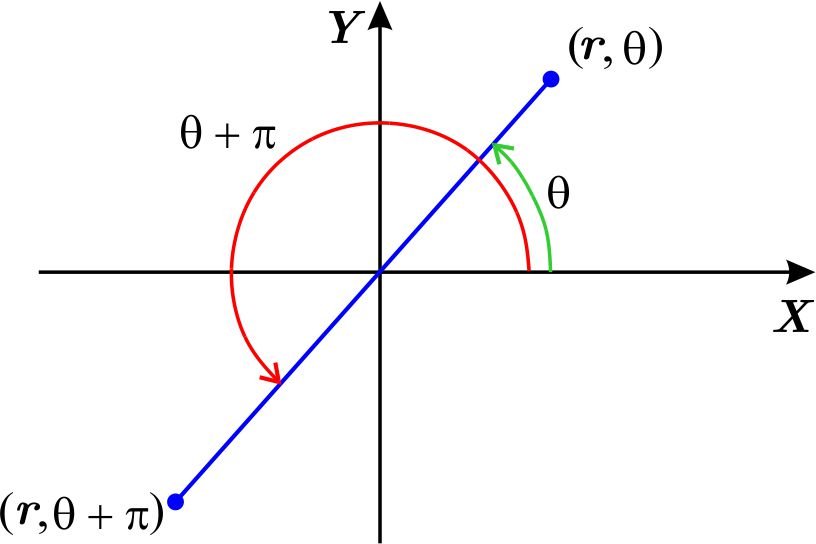
Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto al origen si se cumple que $F\left( r,\theta +\pi \right) =0.$

Por último $\left( r,\dfrac{\pi }{2}-\theta \right) $ es el simétrico de $\left( r,\theta \right) $ con respecto a la recta $y=x.$

ésta es quizá la menos obvia de las observaciones, sin embargo no es difícil convencerse usando la figura siguiente:

El triángulo $\triangle OQP$ es isósceles, entonces la recta $y=x$ es la bisectriz del ángulo $\measuredangle QOP,$ de aquí tenemos que el segmento $PQ$ es perpendicular a la recta y $P$ y $Q$ son simétricos.

Entonces la gráfica de $F\left( r,\theta \right) =0$ es simétrica respecto a la recta $y=x$ si se cumple que $F\left( r,\dfrac{\pi }{2} -\theta \right) =0.$

Ahora es razonable establecer los siguientes cuatro criterios de simetría para gráficas polares:

  1. Simetría respecto al eje $X$. Si al sustituir $\theta $ por $-\theta $ o la pareja $\left( r,\theta \right) $ por la pareja $\left( -r,\pi -\theta \right) $ en una ecuación polar, ésta no se altera, entonces su gráfica polar es simétrica con respecto al eje $X.$

    Observación: En el caso en que al sustituir $\theta $ por $ -\theta $ en una ecuación polar, ésta no se altera, entonces para determinar su gráfica basta considerar valores de $\theta $ no negativos.

  2. Simetría respecto al eje $Y$. Si al sustituir $\theta $ por $\pi -\theta $ o la pareja $\left( r,\theta \right) $ por la pareja $\left( -r,-\theta \right) $ en una ecuación polar, ésta no se altera, entonces su gráfica polar es simétrica con respecto al eje $Y.$

  3. Simetría respecto al origen. Si al sustituir $r$ por $-r$ o $\theta $ por $\pi +\theta $ en una ecuación polar, ésta no se altera, entonces su gráfica polar es simétrica con respecto al origen.

    Observación: En el caso en que al sustituir $r$ por $-r$ en una ecuación polar, ésta no se altera, entonces para determinar su gráfica basta considerar valores de $r$ no negativos.

  4. Simetría respecto a la recta $y=x$. Si al sustituir $\theta $ por $\dfrac{\pi }{2}-\theta $ en una ecuación polar, ésta no se altera, entonces su gráfica polar es simétrica con respecto a la recta $y=x$.

Si se cumplen dos de los tres primeros criterios, se cumple el tercero.

Es frecuente que $F\left( r,\theta \right) $ sea de la forma $F\left( r,\theta \right) =f\left( r\right) -g\left( \theta \right) .$ En tal caso, la ecuación $F\left( r,\theta \right) =0$ es equivalente a $f\left( r\right) =g\left( \theta \right) $ y entonces los criterios de simetría los podemos aplicar a esta última ecuación. Por ejemplo, la curva con ecuación polar $f\left( r\right) =g\left( \theta \right) $ es simétrica respecto al eje $X$ si $f\left( r\right) =g\left( -\theta \right) $, en cuyo caso es aplicable lo dicho en la observación del Criterio 1, y lo es respecto al origen si $f\left( -r\right) =g\left( \theta \right) ,$ en cuyo caso es aplicable lo dicho en la observación del Criterio 3.

Universidad Nacional Autónoma de México