Integrales Dobles

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Regiones en el plano

Definición:

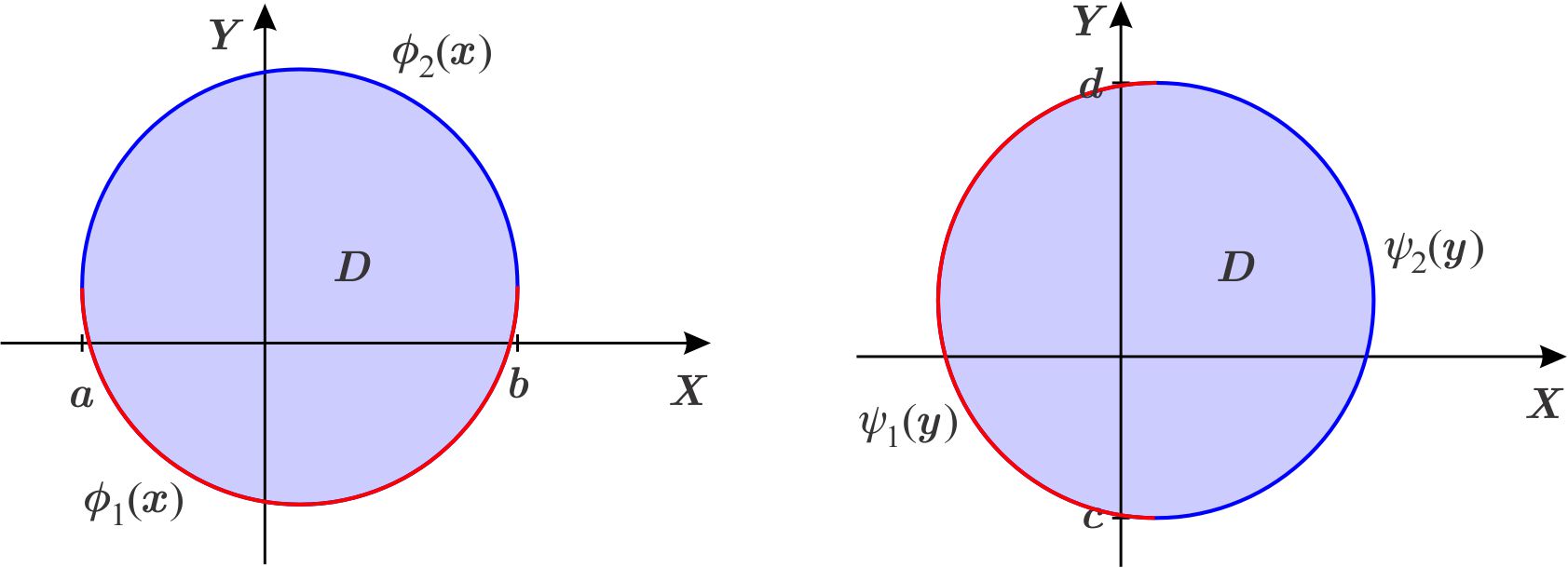
Un conjunto \(D\subset \mathbb{R}^{2}\) es de tipo 1 si existen un intervalo \( \left[ a,b\right]\) y dos funciones continuas \(\phi _{1},\phi _{2}:\left[ a,b\right] \longrightarrow \mathbb{R}\) tales que \begin{equation*} D=\left\{ \left. \left( x,y\right) \,\,\right| \,\,x\in \left[ a,b\right] ,\quad \phi _{1}\left( x\right) \leq y\leq \phi _{2}\left( x\right) \right\} . \end{equation*} En este caso decimos que \(\phi _{1}\) limita la región \(D\) por abajo y que \(\phi _{2}\) la limita por arriba.

 

 

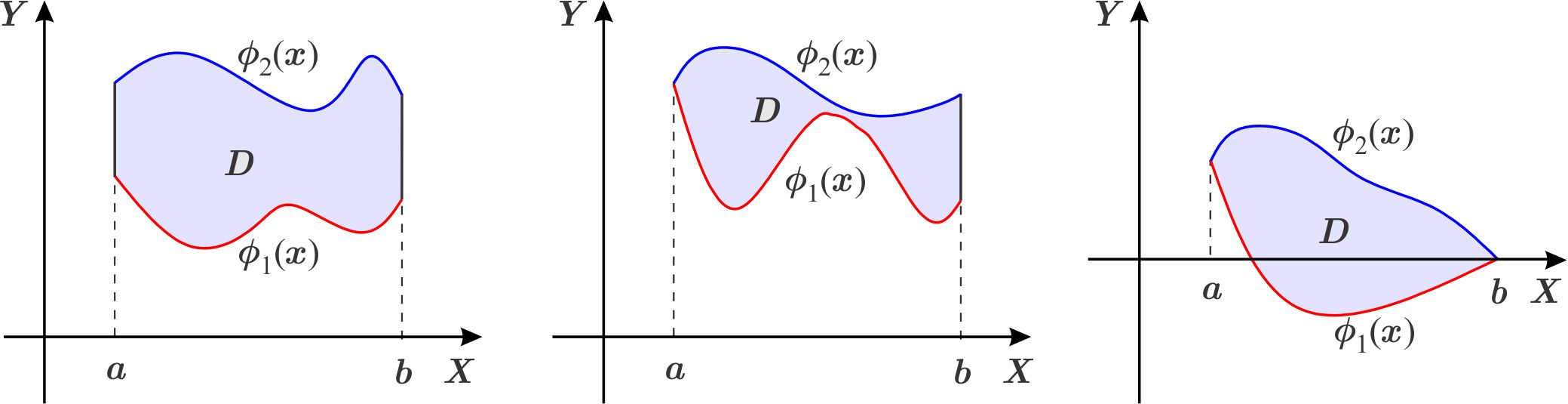
Definición:

Un conjunto \(D\subset \mathbb{R}^{2}\) es de tipo 2 si existen un intervalo \(\left[ c,d\right] \) y dos funciones continuas \(\psi _{1},\psi _{2}:\left[ c,d \right] \longrightarrow \mathbb{R}\) tales que \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ c,d\right] ,\quad \psi _{1}\left( y\right) \leq x\leq \psi _{2}\left( y\right) \right. \right\} . \end{equation*} Noten que ahora la abscisa \(x\) es función de la ordenada \(y\).

En este caso decimos que \(\psi _{1}\) limita a la región \(D\) por la izquierda y que \(\psi _{2}\) la limita por la derecha.

 

 

Definición:

Un conjunto \(D\subset \mathbb{R}^{2}\) es de tipo 3 si es de tipo 1 y de tipo 2.

 

 

Ejemplos

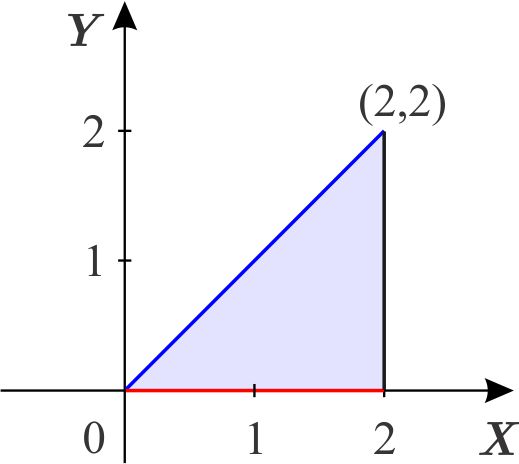
  1. Describe la región sombreada \(D\) de la figura como una de tipo 1.

     

     

    Solución:

    Observamos que todos los puntos \(\left( x,y\right) \) de la región cumplen que \begin{equation*} 0\leq x\leq 2. \end{equation*} Ahora debemos encontrar las dos funciones definidas en el intervalo \(\left[0,2\right] \) del eje \(X\) que limitan a la región. Es decir, las que tienen por gráficas sobre \(\left[ 0,2\right] \) a la recta \(y=0\) y a la recta que une a \(\left( 0,0\right) \) y \(\left( 2,2\right)\) .

    La recta que une los puntos \(\left( 0,0\right) \) y \(\left( 2,2\right) \) es la gráfica de la función \begin{equation*} \phi _{2}\left( x\right) =x. \end{equation*} La línea roja es la gráfica de la función \begin{equation*} \phi _{1}\left( x\right) =0. \end{equation*} Por lo tanto, la región se describe como: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,\,\,x\in \left[ 0,2\right] ,\quad \quad 0\leq y\leq x\right. \right\} . \end{equation*}

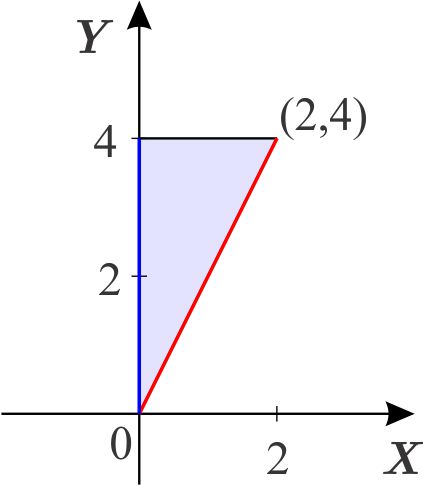
  2. Describe la región sombreada \(D\) de la figura como una de tipo 2.

     

     

    Solución:

    Observamos que todos los puntos \(\left( x,y\right) \) de la región cumplen que \begin{equation*} 0\leq y\leq 4. \end{equation*} Ahora debemos encontrar las dos funciones definidas en el intervalo \(\left[0,4\right] \) del eje \(Y\) que limitan a la región. Es decir, las funciones en la variable \(y\) que tienen por gráficas sobre \(\left[ 0,4 \right] \) a la recta \(x=0\) y a la recta que une a \(\left( 0,0\right) \) y \( \left( 2,4\right) .\)

    La recta que une los puntos \(\left( 0,0\right) \) y \(\left( 2,4\right) \) es la gráfica de la función \(y=2x \), que al poner a \(x\) como función de \(y\) se puede escribir como: \begin{equation*} \psi _{2}\left( y\right) =\dfrac{y}{2}. \end{equation*} La línea azul es la gráfica de la función \begin{equation*} \psi _{1}\left( y\right) =0. \end{equation*} Por lo tanto, la región se describe como: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 0,4\right] ,\quad \quad 0\leq x\leq \dfrac{y}{2}\right. \right\} . \end{equation*}

  3. Describe la región sombreada \(D\) de la figura como de tipo 1 y de tipo 2.

     

     

    Solución:

    Para describir la región como de tipo 1, observamos que para todo \( \left( x,y\right) \) de la región se cumple que \begin{equation*} x\in \left[ 0,3\right] . \end{equation*} La función que limita a la región por abajo es \begin{equation*} \phi _{1}\left( x\right) =0 \end{equation*} y la función \(\phi _{2}\left( x\right) \) que la limita por arriba tiene como gráfica los segmentos de rectas que unen, el punto \(\left( 0,0\right) \) con \(\left( 1,2\right) \) y \(\left( 1,2\right) \) con \(\left( 3,0\right) \); es decir, \(\phi _{2}\) es una función combinada

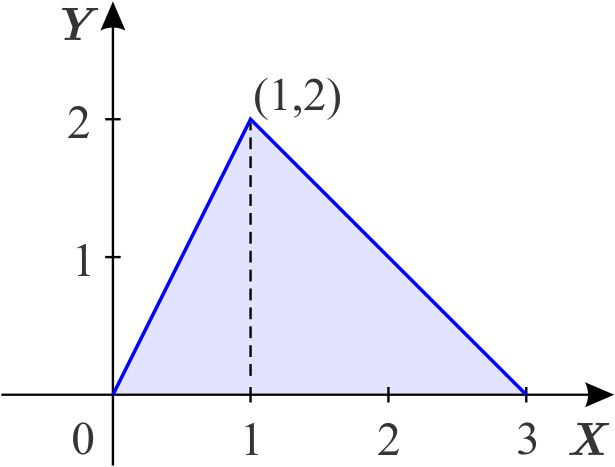
    Así, \begin{equation*} \phi _{2}\left( x\right) =\left\{ \begin{array}{lll} 2x & & \text{si }x\in \left[ 0,1\right] \\ -x+3 & & \text{si }x\in \left[ 1,3\right] \end{array} \right. \end{equation*} La región es: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 0,3\right] ,\quad \quad \phi _{1}\left( x\right) \leq y\leq \phi _{2}\left( x\right) \right. \right\} . \end{equation*} Como \(\phi _{2}\) es una función combinada podemos escribir a \(D\) como la unión de dos subregiones: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 0,1\right] ,\quad \quad 0\leq y\leq 2x\right. \right\} \cup \left\{ \left( x,y\right) \,\left\vert \,x\in \left[1,3\right] ,\quad \quad 0\leq y\leq -x+3\right. \right\} . \end{equation*} Lo que hicimos para obtener esta unión fue dividir el triángulo \(D\) en dos triángulos cortándolo con una recta vertical desde el punto \( \left( 1,0\right) .\)

     

     

    Para describir la región como de tipo 2, observamos que los puntos \( \left( x,y\right) \) de la región cumplen que \begin{equation*} 0\leq y\leq 2. \end{equation*} La recta que limita por la izquierda a \(D\) es la que une los puntos \(\left( 0,0\right) \) y \(\left( 1,2\right) ,\) la cual tiene ecuación \begin{equation*} y=2x, \end{equation*} de donde, \begin{equation*} x=\psi _{1}\left( y\right) =\dfrac{y}{2}. \end{equation*} La recta que limita por la derecha a \(D\) es la que une los puntos \(\left( 1,2\right) \) y \(\left( 3,0\right) \), la cual tiene ecuación \begin{equation*} y=-x+3, \end{equation*} de donde, \begin{equation*} x=\psi _{2}\left( y\right) =-y+3. \end{equation*} Por lo tanto, la región se describe como: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 0,2\right] ,\quad \quad \dfrac{y}{2}\leq x\leq -y+3\right. \right\} . \end{equation*}

  4. Describe la región \(D\) limitada por las funciones \(y=2x^{2}+1\) y \( y=2x+5. \)

     

    Solución:

    La gráfica de \(\phi _{1}\left( x\right) =2x^{2}+1\) es una parábola con vértice \(\left( 0,1\right) \) y la gráfica de \(\phi _{2}\left( x\right) =2x+5\) es una recta. Al graficar las funciones

     

     

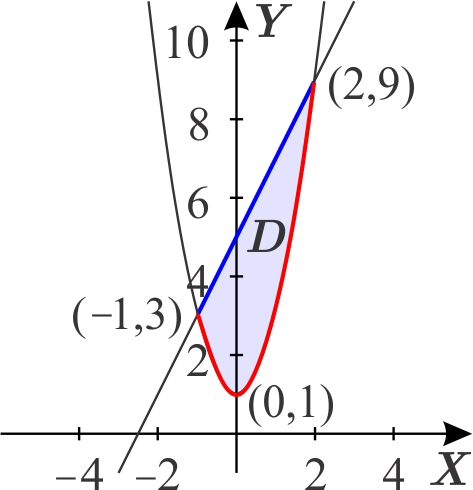
    observamos que \begin{equation*} 2x^{2}+1\leq 2x+5 \end{equation*} para todo \(x \), en la región limitada por las curvas.

    Encontramos los puntos donde se cortan estas gráficas. \begin{eqnarray*} 2x^{2}+1 &=&2x+5 \\ 2x^{2}-2x-4 &=&0 \\ x^{2}-x-2 &=&0 \\ \left( x+1\right) \left( x-2\right) &=&0, \end{eqnarray*} de donde sus abscisas son \begin{equation*} x=-1,\quad \quad \quad x=2, \end{equation*} y sus ordenadas \begin{equation*} 2\left( -1\right) ^{2}+1=3\quad \quad \quad \text{y} \quad \quad \quad 2\times 2+5=9 \end{equation*} respectivamente. Los puntos de intersección son \begin{equation*} \left( -1,3\right) \quad \quad \quad \text{y} \quad \quad \quad \left( 2,9\right) . \end{equation*}

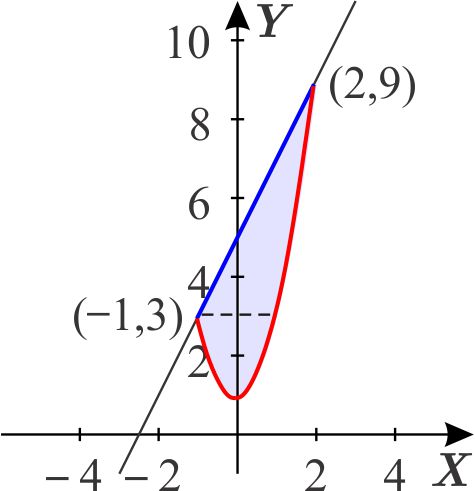
    La función \(\psi _{1}:\left[ 1,9\right] \rightarrow \mathbb{R}\) que limita a la región por la izquierda es una función combinada. Es la combinación de dos funciones \(\psi _{11}\ \) y \(\psi _{12} \). La primera, \( \psi _{11},\) está definida en el intervalo \(\left[ 1,3\right] \) del eje \( Y\) y tiene por gráfica el arco de la parábola \(y=2x^{2}+1\) que une los puntos \(\left( 0,1\right) \) y \(\left( -1,3\right) \) y la segunda, \(\psi _{12} \), es la función definida en \(\left[ 3,9\right] \) del eje \(Y\) y que tiene por gráfica el segmento de recta que une los puntos \(\left( -1,3\right) \) y \(\left( 2,9\right) . \)

     

     

    Entonces \begin{equation*} \psi _{1}\left( y\right) =\left\{ \begin{array}{lll} \psi _{11}\left( y\right) & & \text{si }y\in \left[ 1,3\right] \\ \psi _{12}\left( y\right) & & \text{si }y\in \left[ 3,9\right] \end{array} \right. \end{equation*} Para obtener la regla de correspondencia de \(\psi _{11}\) despejamos \(x\) de la ecuación \(y=2x^{2}+1 \): \begin{eqnarray} y-1 &=&2x^{2} \notag \\ \dfrac{y-1}{2} &=&x^{2} \notag \\ \sqrt{\dfrac{y-1}{2}} &=&\left\vert x\right\vert . \label{1} \tag{1} \end{eqnarray} Observamos que \(x\leq 0\) para los puntos del arco de parábola que une \( \left( 0,1\right) \) y \(\left( -1,3\right) \), por lo que \begin{equation*} \psi _{11}\left( y\right) =-\sqrt{\dfrac{y-1}{2}} \end{equation*} para \(y\in \left[ 1,3\right] \).

    La regla de correspondencia de \(\psi _{12}\) la obtenemos despejando \(x\) de la ecuación de la recta \(y=2x+5 \) \begin{equation*} x=\frac{1}{2}\left( y-5\right) . \end{equation*} Así, \begin{equation*} \psi _{12}\left( y\right) =\frac{1}{2}\left( y-5\right) \end{equation*} para \(y\in \left[ 3,9\right] \).

    Entonces, \begin{equation*} \psi _{1}\left( y\right) =\left\{ \begin{array}{lll} -\sqrt{\dfrac{y-1}{2}} & & \text{si }y\in \left[ 1,3\right] \\ & & \\ \dfrac{1}{2}\left( y-5\right) & & \text{si }y\in \left[ 3,9\right] \end{array} \right. \end{equation*} Por la derecha la región está limitada por la función \(\psi _{2} \) definida en el intervalo \(\left[ 1,9\right] \) del eje \(Y\) que tiene por gráfica el arco de la parábola \(y=2x^{2}+1\) que une a su vértice \( \left( 0,1\right) \) con el punto \(\left( 2,9\right) .\) Por (\ref{1}) y debido a que los puntos \(\left( x,y\right) \) de ese arco cumplen que \(x\geq 0,\) obtenemos \begin{equation*} \psi _{2}\left( y\right) =\sqrt{\dfrac{y-1}{2}} \end{equation*} para \(y\in \left[ 1,9\right] . \)

    La región \(D\) considerada es de tipo 2: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,\,y\in \left[ 1,9\right] ,\quad \quad \psi _{1}\left( y\right) \leq x\leq \psi _{2}\left( y\right) \right. \right\} . \end{equation*} Como \(\psi _{1}\) es una función combinada podemos presentar a \(D\) como la unión de dos regiones de tipo 2 \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{equation*} D_{1}=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 1,3\right] ,\quad \quad -\sqrt{\dfrac{y-1}{2}}\leq x\leq \sqrt{\dfrac{y-1}{2}}\right. \right\} \end{equation*} y \begin{equation*} D_{2}=\left\{ \left( x,y\right) \,\left\vert \,\,y\in \left[ 3,9\right] ,\quad \quad \dfrac{y-5}{2}\leq x\leq \sqrt{\dfrac{y-1}{2}}\right. \right\} . \end{equation*}

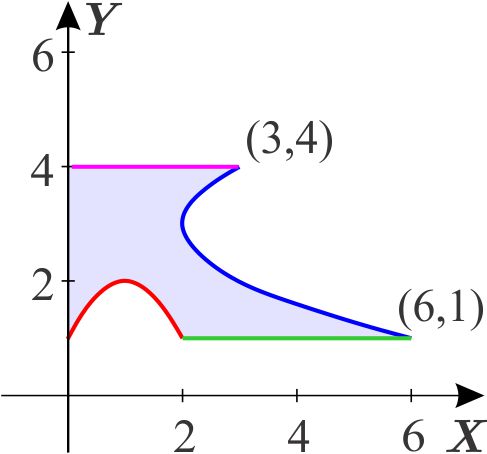
  5. Describe la región sombreada \(D\) de la figura, limitada por: el eje \(Y,\) las rectas \(y=1\) y \(y=4\) y por las parábolas \(y=-x^{2}+2x+1\) y \( x=\left( y-3\right) ^{2}+2,\) como unión de regiones de tipo 1 y 2.

     

     

    Solución:

    El vértice de la parábola \(x=\left( y-3\right) ^{2}+2\) tiene coordenadas \(\left( 2,3\right) . \) Trazamos la recta \(x=2.\)

     

     

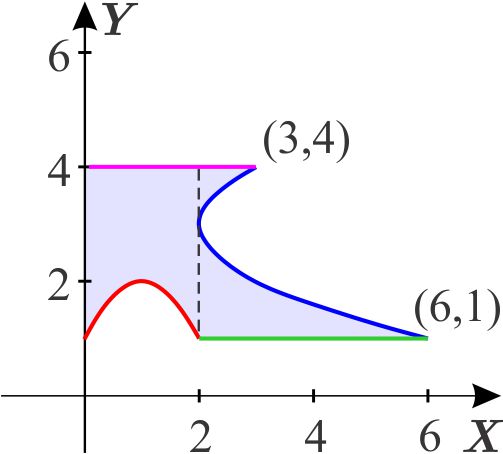
    La región está dividida en dos regiones, llamando \(D_{1}\) a la de la izquierda que es de tipo 1, tenemos \begin{equation*} D_{1}=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 0,2\right] ,\quad \quad -x^{2}+2x+1\leq y\leq 4\right. \right\} . \end{equation*} Si llamamos \(D_{2}\) a la región de la derecha que es de tipo 2, tenemos: \begin{equation*} D_{2}=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 1,4\right] ,\quad \quad 2\leq x\leq \left( y-3\right) ^{2}+2\right. \right\} . \end{equation*} La región dada es \begin{equation*} D=D_{1}\cup D_{2}. \end{equation*}

  6. Describe la región que se encuentra dentro de \(r=3\) y arriba de \(r= \dfrac{3}{\ \text{sen}\ \theta -\cos \theta } \), donde éstas son ecuaciones polares.

     

    Solución:

    La gráfica polar de \(r=3\) corresponde a un círculo con centro en el origen y radio \(3.\) (Ver Coordenadas Polares - Círculos).

    Para dibujar la otra curva en el plano cartesiano \(XY,\) escribimos las ecuaciones usando el cambio de coordenadas \begin{eqnarray*} x &=&r\cos \theta \\ y &=&r\ \text{sen}\ \theta . \end{eqnarray*} Entonces \begin{eqnarray*} r &=&\dfrac{3}{\ \text{sen}\ \theta -\cos \theta } \\ r\left( \ \text{sen}\ \theta -\cos \theta \right) &=&3 \\ r\ \text{sen}\ \theta -r\cos \theta &=&3 \\ y-x &=&3 \\ y &=&x+3 \end{eqnarray*} que corresponde a la recta con pendiente \(1,\) que pasa por el punto de coordenadas \(\left( 0,3\right) \) (Ver Coordenadas Polares - Rectas). .

    Dibujamos las gráficas de ambas curvas y sombreamos la región buscada.

     

     

    Describiéndola como de tipo 2, tenemos: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 0,3\right] ,\quad \quad -\sqrt{9-y^{2}}\leq x\leq y-3\right. \right\} . \end{equation*} Observación:

    Cuando nos refiramos al plano cartesiano estaremos usando las coordenadas rectangulares de sus puntos y las ecuaciones rectangulares de las curvas, y cuando hablemos del plano polar estaremos considerando las coordenadas polares de los puntos y las ecuaciones polares de las curvas.

  7. Considera la región \(D\) acotada por la parábola \(y=4-\dfrac{1}{4}\left( x+2\right) ^{2} \), la recta \(y=\dfrac{3}{2}x+3 \) y el eje \(X.\) Escríbela:

     

    Solución:

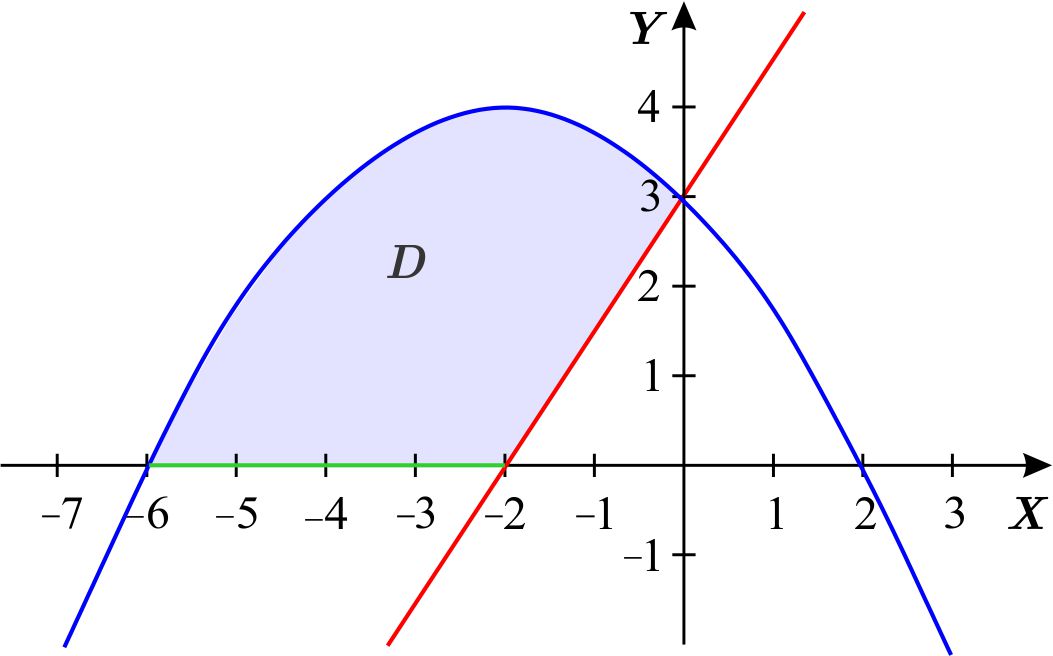
    La ecuación de la parábola la escribimos como \begin{equation*} y-4=-\dfrac{1}{4}\left( x+2\right) ^{2}, \end{equation*} y de esto identificamos que se trata de una parábola vertical, que abre hacia abajo y cuyo vértice está en el punto \(\left( -2,4\right) . \)

    La recta \(y=\dfrac{3}{2}x+3\) pasa por el punto \(\left( 0,3\right) \) y tiene pendiente \(\dfrac{3}{2}. \)

    Dibujamos las gráficas para ver la región a considerar

     

     

    Para describir la región como unión de regiones de tipo 1, dividimos la región de la siguiente manera:

     

     

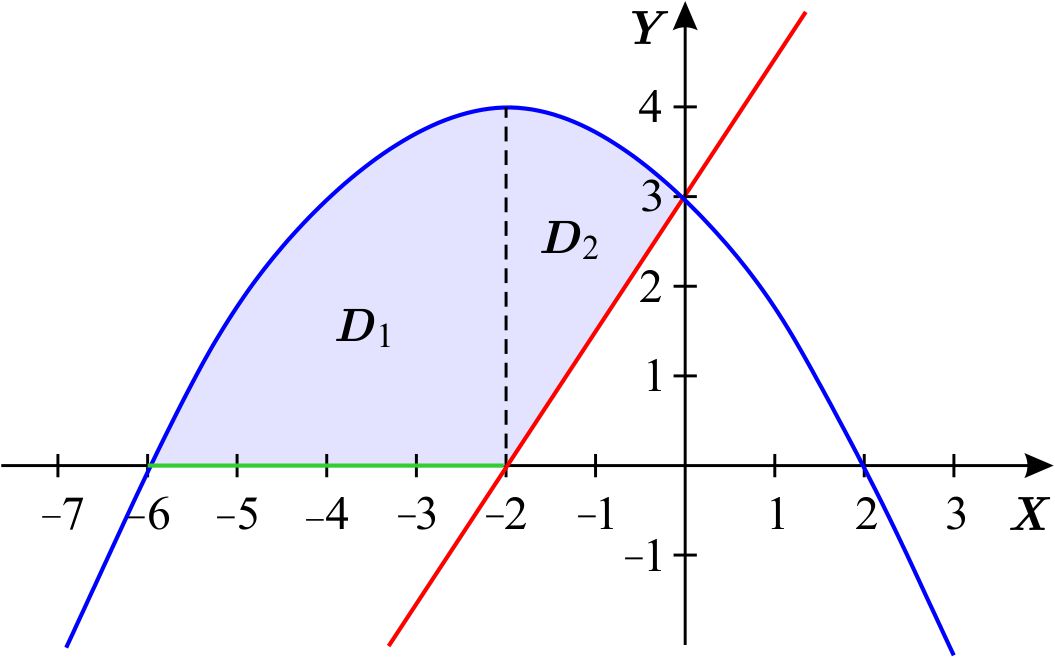
    entonces \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{equation*} D_{1}=\left\{ \left( x,y\right) \left\vert \,x\in \left[ -6,-2\right] ,\quad \quad 0\leq y\leq 4-\dfrac{1}{4}\left( x+2\right) ^{2}\right. \right\} \end{equation*} y \begin{equation*} D_{2}=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ -2,0\right] ,\quad \quad \dfrac{3}{2}x+3\leq y\leq 4-\dfrac{1}{4}\left( x+2\right) ^{2}\right. \right\} . \end{equation*} Para describir la región como unión de regiones de tipo 2, dividimos la región de la siguiente manera:

     

     

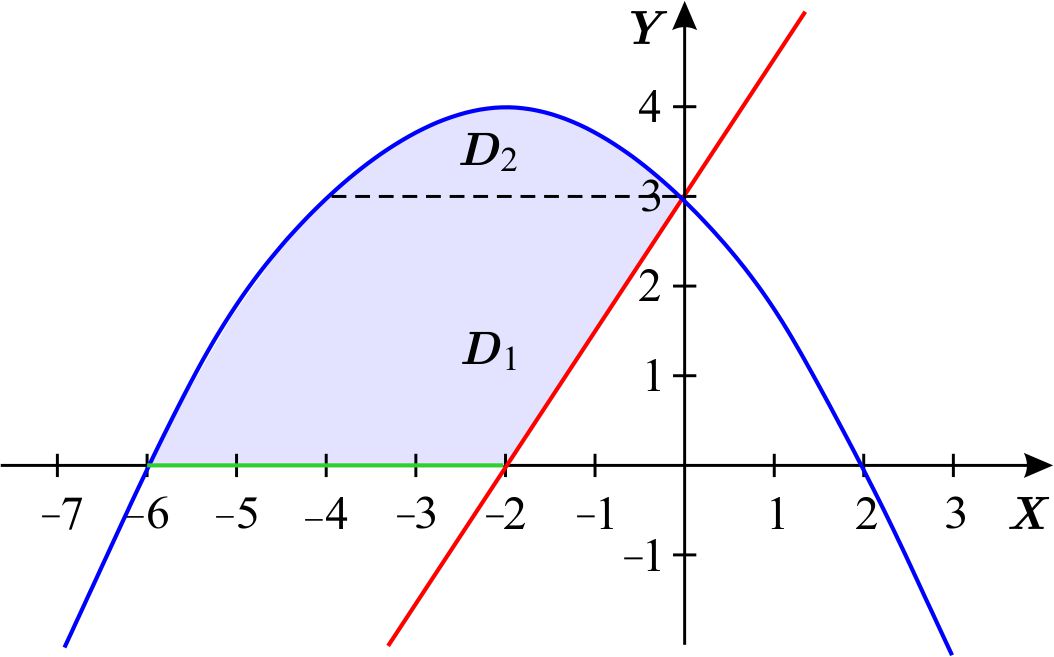
    Entonces \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{equation*} D_{1}=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 0,3\right] ,\quad \quad -2-\sqrt{16-4y}\leq x\leq \dfrac{2}{3}y-2\right. \right\} \end{equation*} y \begin{equation*} D_{2}=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ 3,4\right] ,\quad \quad -2-\sqrt{16-4y}\leq x\leq -2+\sqrt{16-4y}\right. \right\} . \end{equation*}

Ejercicios

En los ejercicios 1 a 5 llama \(D\) a la región indicada y descríbela como de tipo 1 y/o de tipo 2, o bien como la unión de cada uno de los tipos.

     
  1. El triángulo con vértices \(\left( -2,0\right) ,\left( 0,3\right) \) y \(\left( 2,0\right) . \)
     
  2. El triángulo con vértices \(\left( -3,4\right) ,\left( 0,0\right) \) y \(\left( 3,4\right) . \)
     
  3. La región acotada por las parábolas \(y=\dfrac{\left( x+4\right) ^{2}}{8}\) y \(y=8\sqrt{x+4}.\) Los puntos de intersección de las parábolas son \(\left( -4,0\right) \) y el \(\left( 12,32\right) . \)
     
  4. La región acotada por las funciones \(y=\dfrac{x^{2}}{4}+1\) y \( y=x+4. \)
     
  5. La región acotada por el eje \(X,\) la función \(y=\sqrt{x+5}\) y la recta que pasa por el punto \(\left( 4,3\right) \) y tiene pendiente \(- \dfrac{1}{2}. \)
     
  6. La región acotada por las funciones \(y=\ \text{sen}\ x\) y \(y=\cos x \) con \(x\in \left[ -\dfrac{\pi }{2},\pi \right] \):

       
    1. ¿Es de tipo 1? Si tu respuesta es afirmativa describe la región.
       
    2. ¿Es de tipo 2? Si tu respuesta es afirmativa describe la región.

     
  7. La región acotada por las parábolas \(y=5x^{2}-5\) y \(y=x^{2}+4. \)

       
    1. Escribe la región como de tipo 1.
       
    2. Escribe la región como unión de regiones de tipo 2.

     
  8. Describe el anillo que forman los círculos \(\left( x-2\right) ^{2}+y^{2}=25\) y \(\left( x-2\right) ^{2}+y^{2}=9\) como unión de regiones de tipo 1 o de tipo 2.
     
  9. La región acotada por las funciones \(y=2\ln x\) y \(y=5\ln x,\) la recta \(x=8\) y \(y\geq 0. \)
     
  10. La región \(D\) es la que se encuentra dentro de la elipse \( 3x^{2}+4y^{2}+6x-45=0\) y dentro de la hipérbola \(3x^{2}-y^{2}+6x=0.\) Los puntos de intersección de las cónicas son \(A\left( -3,3\right) , \) \( B\left( 1,3\right) , \) \(C\left( -3,-3\right) \) y \(E\left( 1,-3\right) . \) Describe la región \(D\) como de tipo 1.
     
  11. La región \(D\) es la que se encuentra fuera del semicírculo superior con centro en \(\left( 3,0\right) \) y radio \(3,\) y la parábola \( y=\sqrt{12x} \). Describe la región \(D\) como de tipo 1 y como de tipo 2.
     
  12. La región \(D\) es la que se encuentra dentro del círculo \( x^{2}+y^{2}=25\) y fuera de la hipérbola \(x^{2}-y^{2}=7.\) Describe la región \(D\) como de tipo 2.
Universidad Nacional Autónoma de México