Coordenadas Polares

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Rectas

Analizaremos ahora, en términos de las coordenadas polares, el tipo de curva más simple, la recta.

De entre las rectas, en coordenadas cartesianas las de ecuación más simple son las paralelas a los ejes y las que pasan por el origen.

Las que son paralelas al eje \(Y\) tienen ecuación \begin{equation*} x=a,\qquad a\in \mathbb{R} \end{equation*} esto es, la recta es vertical y corta al eje \(X\) en el punto \(\left( a,0\right) \). Entonces en coordenadas polares la ecuación es \begin{equation*} r\cos \theta =a \end{equation*} geométricamente:

para cualquier punto \(P\left( r,\theta \right) \) de esta recta, el valor que tome \(r\cos \theta \) será \(a.\)
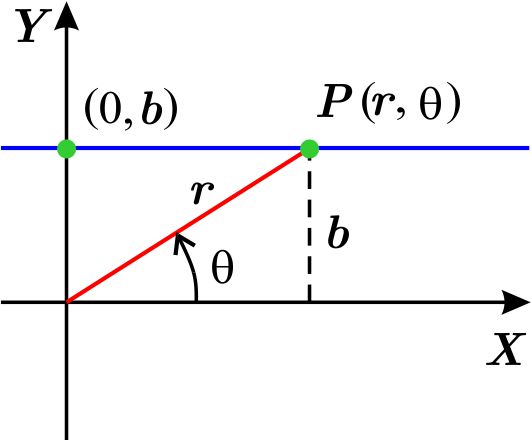
Las rectas paralelas al eje \(X\) tienen ecuación cartesiana: \begin{equation*} y=b,\qquad b\in \mathbb{R} \end{equation*} ésta es una recta horizontal que corta al eje \(Y\) en el punto \(\left( 0,b\right) ,\) haciendo el cambio a coordenadas polares obtenemos: \begin{equation*} r\ \text{sen}\ \theta =b \end{equation*} geométricamente:

para cualquier punto \(P\left( r,\theta \right) \) de esta recta, el valor que tome \(r\ \text{sen}\ \theta \) será \(b.\)
Ahora bien, una recta no vertical que pasa por el origen tiene ecuación cartesiana \begin{equation*} y=ax,\qquad a\in \mathbb{R} \end{equation*} que se traduce en coordenadas polares a: \begin{equation*} r\ \text{sen}\ \theta =ar\cos \theta , \end{equation*} es decir, \begin{eqnarray*} \ \text{sen}\ \theta & = & a\cos \theta \\ \dfrac{\ \text{sen}\ \theta }{\cos \theta } & = & a \\ \tan \theta & = & a \\ \theta & = & \arctan a \end{eqnarray*} es decir, \(\theta \) constante.

Así, en coordenadas polares, la ecuación de una recta que pase por el origen es: \begin{equation*} \theta =\theta _{0},\qquad \theta _{0}=\text{constante} \end{equation*} esta es la recta que forma un ángulo \(\theta _{0}\) con el eje \(X.\)

Ejemplos

Encuentra la ecuación polar de la recta \(y=x\).
Solución:
Si procedemos como antes: \begin{eqnarray*} y & = & x \\ r\ \text{sen}\ \theta & = & r\cos \theta \\ \ \text{sen}\ \theta & = & \cos \theta \\ \dfrac{\ \text{sen}\ \theta }{\cos \theta } & = & 1 \\ \tan \theta & = & 1, \end{eqnarray*} entonces la ecuación polar es \begin{equation*} \theta =\dfrac{\pi }{4}. \end{equation*}
Considera la ecuación polar de la recta \(\theta =\dfrac{\pi }{3}.\) Encuentra la ecuación cartesiana.
Solución:
Sustituyendo \(\theta =\dfrac{\pi }{3}\) en la ecuación \(\dfrac{y}{x}=\tan \theta ,\) tenemos \begin{equation*} \dfrac{y}{x}=\tan \dfrac{\pi }{3}=\dfrac{\ \text{sen}\ \dfrac{\pi }{3}}{\cos \dfrac{\pi }{3}}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}}=\sqrt{3} \end{equation*} de donde: \begin{equation*} y=\sqrt{3}x. \end{equation*}

Consideremos la ecuación general de una recta no vertical. \begin{equation*} y=ax+b,\qquad a,b\in \mathbb{R},\qquad a\neq 0 \end{equation*} esta es la recta que corta al eje \(Y\) en \(\left( 0,b\right) \) y que tiene pendiente \(a\). Como \(a\neq 0\), entonces la recta corta al eje \(X\) en \( \left( -\dfrac{b}{a},0\right) .\) Mediante la sustitución \begin{equation*} x=r\cos \theta ,\qquad y=r\ \text{sen}\ \theta \end{equation*}

obtenemos la ecuación general en coordenadas polares de las rectas no verticales: \begin{equation*} r\ \text{sen}\ \theta =ar\cos \theta +b, \end{equation*} es decir \begin{eqnarray} ar\cos \theta -r\ \text{sen}\ \theta +b & = & 0 \notag \\ r\left( a\cos \theta -\ \text{sen}\ \theta \right) +b & = & 0 \label{Ecgral} \tag{3} \end{eqnarray}

Ejemplos

Dibuja la gráfica de la recta dada por la ecuación \(r\ \text{sen}\ \theta =-2.\)
Solución:
Se trata de una recta paralela al eje \(X\)
Dibuja la gráfica de la recta dada por la ecuación \begin{equation*} r=\dfrac{3}{\ \text{sen}\ \theta -\cos \theta }. \end{equation*}
Solución:
Llevamos la ecuación a la forma general \begin{eqnarray*} r\left( \ \text{sen}\ \theta -\cos \theta \right) & = & 3 \\ r\left( \ \text{sen}\ \theta -\cos \theta \right) -3 & = & 0 \\ r\left( \cos \theta -\ \text{sen}\ \theta \right) +3 & = & 0 \end{eqnarray*} Hemos llevado la ecuación a la forma general de la recta en coordenadas polares (\ref{Ecgral}), donde \(a=1,\) \(b=3.\) Se trata entonces de la recta que corta al eje \(Y\) en \(\left( 0,3\right) \) y al eje \(X\) en \(\left( -3,0\right) ,\) es decir, la recta \(y=x+3\).

Universidad Nacional Autónoma de México