Coordenadas Polares Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Lemniscatas

Ejemplos

1. Dibujar la gráfica de $r^{2}=a^{2}\cos \left( 2\theta \right) $.

   Notamos que esta ecuación es del tipo $f\left( r\right) =g\left( \theta \right) $, donde $f\left( r\right) =r^{2}$ y $g\left( \theta \right) =a^{2}\cos \left( 2\theta \right) $.

   Para ahorrar trabajo, utilizaremos los criterios de simetría.

   • Al cambiar $\theta $ por $-\theta $, obtenemos: \begin{equation*} r^{2}=a^{2}\cos \left( -2\theta \right) =a^{2}\cos \left( 2\theta \right) , \end{equation*} entonces la gráfica es simétrica con respecto al eje $X$.

     Por el primer criterio de simetría basta considerar valores de $\theta $ no negativos para obtener la gráfica correspondiente.

   • Al cambiar $\theta $ por $\pi -\theta $, obtenemos: \begin{eqnarray*} r^{2} &=&a^{2}\cos \left( 2\left( \pi -\theta \right) \right) \\ r^{2} &=&a^{2}\cos \left( 2\pi -2\theta \right) \\ r^{2} &=&a^{2}\cos \left( 2\theta \right) , \end{eqnarray*} entonces la gráfica es simétrica con respecto al eje $Y$.
   • Puesto que se cumplen los dos primeros criterios, automáticamente se cumple el tercero, es decir, la gráfica es simétrica con respecto al origen y por el tercer criterio de simetría basta considerar valores de $r$ no negativos para obtener la gráfica correspondiente.
   • Al cambiar $\theta $ por $\dfrac{\pi }{2}-\theta $, obtenemos: \begin{equation*} r^{2}=a^{2}\cos \left( \dfrac{\pi }{2}-\theta \right) =a^{2} \ \text{sen}\ \theta , \end{equation*} es decir, el cuarto criterio no nos da información adicional.

   Debido a que la gráfica es simétrica con respecto a ambos ejes, basta con obtener la gráfica en el primer cuadrante y reflejar con respecto a cada eje.

   Consideremos en el plano cartesiano $\Theta R$ la gráfica de $r=a\sqrt{ \cos \left( 2\theta \right) }$ en $\left[ 0,\dfrac{\pi }{4}\right] .$

   

   Así, sustituyendo $\theta =0$ en la ecuación, obtenemos $r=a$. Ahora, si $\theta $ varía entre $0$ y $\dfrac{\pi }{4}$, $a\sqrt{\cos \left( 2\theta \right) }$ disminuye de $a$ a $0,$ de $\dfrac{\pi }{4}$ a $ \dfrac{\pi }{2},$ $\cos \left( 2\theta \right) $ es negativo y no hay valores reales de $r$ que satisfagan $r=a\sqrt{\cos \left( 2\theta \right) } , $ la gráfica polar en el primer cuadrante es:

   

   usando las simetrías se obtiene:

   
2. Dibujar la gráfica de $r^{2}=-a^{2} \ \text{sen}\left( 2\theta \right) .$

   Solución:

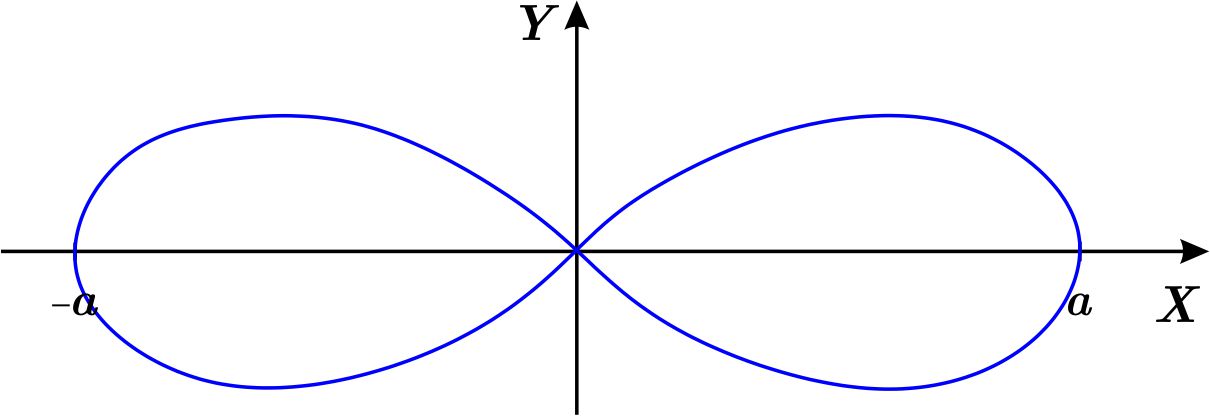
   Notamos que esta ecuación es del tipo $f\left( r\right) =g\left( \theta \right) $, donde $f\left( r\right) =r^{2}$ y $g\left( \theta \right) =-a^{2} \ \text{sen}\left( 2\theta \right) $.

   Aplicamos los criterios de simetría:

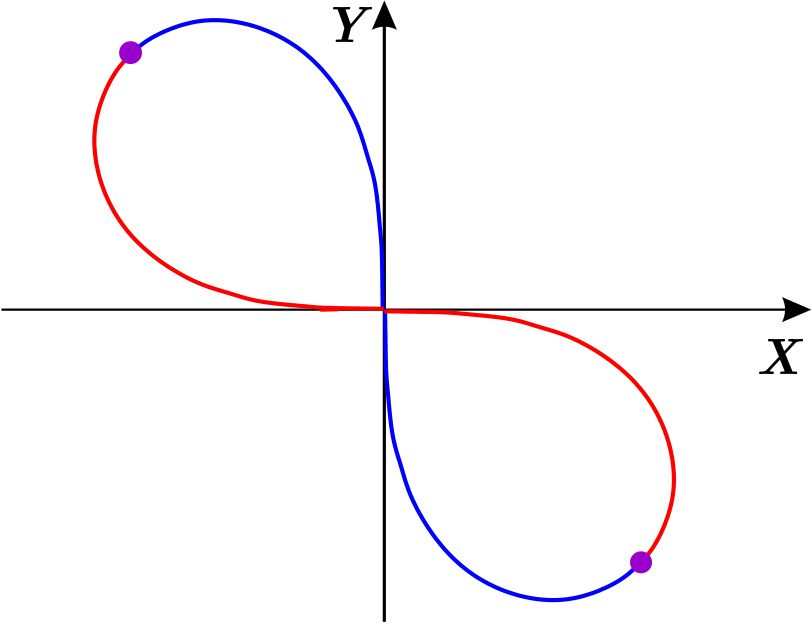
   El primer criterio no se satisface, pues si sustituimos $\theta $ por $ -\theta ,$ tenemos \begin{eqnarray*} r^{2} &=&-a^{2} \ \text{sen}\left( 2\left( -\theta \right) \right) \\ &=&-a^{2} \ \text{sen}\left( -2\theta \right) \\ &=&a^{2} \ \text{sen}\left( 2\theta \right) \end{eqnarray*} o bien, si sustituimos la pareja $\left( r,\theta \right) $ por la pareja $\left( -r,\pi -\theta \right) ,$ tenemos \begin{eqnarray*} \left( -r\right) ^{2} &=&-a^{2} \ \text{sen}\left( 2\left( \pi -\theta \right) \right) \\ r^{2} &=&-a^{2} \ \text{sen}\left( 2\pi -2\theta \right) \\ r^{2} &=&-a^{2} \ \text{sen}\left( -2\theta \right) \\ r^{2} &=&a^{2} \ \text{sen}\left( 2\theta \right) . \end{eqnarray*} y el criterio tampoco se satisface. Por tanto, este primer criterio no da información

   El segundo criterio tampoco se cumple, ya que si sustituimos $\theta $ por $ \pi -\theta ,$ de la misma manera que antes, tenemos \begin{eqnarray*} r^{2} &=&-a^{2} \ \text{sen}\left( 2\left( \pi -\theta \right) \right) \\ &=&-a^{2}\left( - \ \text{sen}\left( 2\theta \right) \right) \\ &=&a^{2} \ \text{sen}\left( 2\theta \right) . \end{eqnarray*} o bien, al sustituir la pareja $\left( r,\theta \right) $ por la pareja $ \left( -r,-\theta \right) ,$ tenemos \begin{eqnarray*} \left( -r\right) ^{2} &=&-a^{2} \ \text{sen}\left( 2\left( -\theta \right) \right) \\ r^{2} &=&-a^{2} \ \text{sen}\left( -2\theta \right) \\ r^{2} &=&a^{2} \ \text{sen}\left( 2\theta \right) \end{eqnarray*} Por tanto, este segundo criterio tampoco da información

   El tercero se cumple, ya que al cambiar $r$ por $-r$ la ecuación no se altera. Entonces la gráfica es simétrica respecto al origen y por la observación del tercer criterio, basta considerar valores de $r$ no negativos para obtener la gráfica correspondiente.

   Finalmente, cambiando $\theta $ por $\dfrac{\pi }{2}-\theta $ tenemos \begin{eqnarray*} r^{2} &=&-a^{2} \ \text{sen}\left( 2\left( \dfrac{\pi }{2}-\theta \right) \right) \\ r^{2} &=&-a^{2} \ \text{sen}\left( \pi -2\theta \right) \\ r^{2} &=&-a^{2}\left( \ \text{sen}\ \pi \cos \left( 2\theta \right) -\cos \pi \ \text{sen}\left( 2\theta \right) \right) \\ r^{2} &=&-a^{2} \ \text{sen}\left( 2\theta \right) . \end{eqnarray*} Entonces la gráfica es simétrica con respecto a la recta $y=x.$

   Dibujamos $r=\sqrt{-a^{2} \ \text{sen}\left( 2\theta \right) }$ en el plano cartesiano $\Theta R$ en el intervalo $\left[ 0,\pi \right] $

   

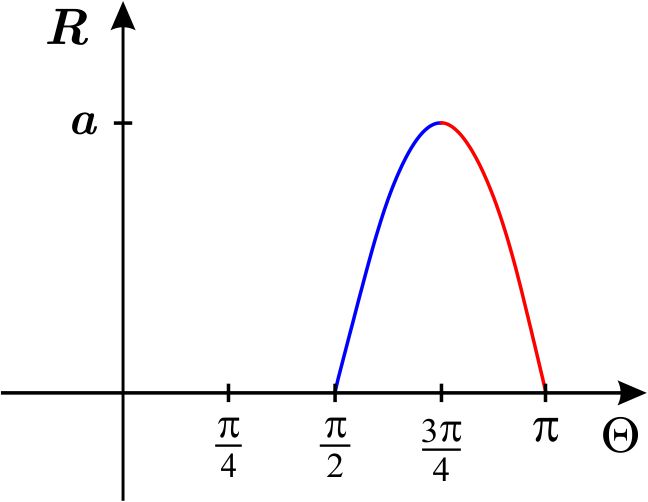
   En el intervalo $\left[ \dfrac{\pi }{2},\dfrac{3\pi }{4}\right] ,$ $\sqrt{ -a^{2} \ \text{sen}\left( 2\theta \right) }$ aumenta de $0$ a $a$ y en el intervalo $\left[ \dfrac{3\pi }{4},\pi \right] ,$ $\sqrt{-a^{2} \ \text{sen}\ \left( 2\theta \right) }$ disminuye de $a$ a $0,$ la gráfica polar en los dos primeros cuadrantes es, por consiguiente:

   

   Reflejando con respecto a la recta $y=x$ obtenemos la gráfica buscada

   

Ejercicios

1. $r^{2}=-16\cos \left( 2\theta \right) .$

2. $r^{2}=9 \ \text{sen}\left( 2\theta \right) .$

3. $r^{2}=-4 \ \text{sen}\left( 2\theta \right) .$

4. $r^{2}=9\cos \left( 2\theta \right) .$

5. $r^{2}=-8\cos \left( 2\theta \right) .$

6. $r^{2}=-2 \ \text{sen}\left( 2\theta \right) .$