Teorema de Taylor

En este apartado, extenderemos las ideas que experimentamos en el apartado anterior con la función arctan(x), hasta la formulación del Teorema de Taylor, el cual establece una relación bastante buena entre una función y su polinomio de Taylor.

Una definición

Algo importante

Sería muy importante poder calcular una expresión general para el resto , sobre todo para poder cuantificarlo y así poder saber la proximidad de . Por ejemplo, en el apartado anterior vimos que:

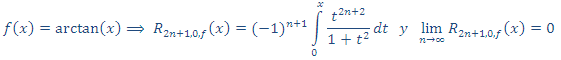
Calculando una expresión para el resto

Empezaremos con el caso más sencillo para n = 0

Ahora para n = 1

Ahora para n = 2

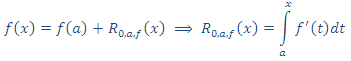
Forma general del resto

Siguiendo con el procedimiento anterior de manera recursiva, podemos intuir la forma general del resto, como lo demostraremos enseguida por el método de inducción matemática, incluyendo la hipótesis de que , debido a los requerimientos del teorema de integración por partes:

Estamos ahora en posibilidad de abordar nuestro teorema más general y más importante, en cuya demostración utilizaremos teoremas importntes del tema de derivadas como el Teorema del Valor Medio y el Teorema del Valor Medio de Cauchy. Puedes dar clic en cada uno de ellos, si gustas recordarlos.

Teorema 4 (teorema de Taylor)

En el siguiente apartado veremos como estimar restos para algunas de las funciones más conocidas. Igualmente veremos algunas aplicaciones de este teorema.