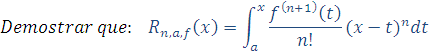
Demostración (Utilizaremos el método de inducción matemática, empezando desde n = 0)
1) Primero veamos que se cumple para n = 0.
Sabemos que: ![]()
Y por el teorema fundamental del Cálculo, tenemos que: ![]()
De donde nos queda que: ![]()
Y así, de (1) y (2) nos queda que: ![]()
2) Supongamos que se cumple para n = k. Es decir, supongamos que:
![]()
3) Haremos ver que se cumple para n = k + 1. Utilizaremos la hipótesis de inducción (hi).
Calculemos la integral en (hi), utilizando el método de integración por partes, haciendo:
![]()
de donde: ![]()
Recordando el teorema de integración por partes:
![]()
Al sustituir las expresiones (3) y (4) en (hi) nos queda:
![]()
Como: ![]() , entonces nos queda:
, entonces nos queda:
![]()
Ahora bien, sabemos que para n = k tenemos que: 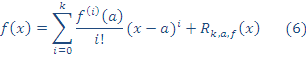
Sustituyendo (5) en la expresión (6), nos queda:
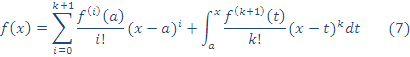
Por tanto de (7), se puede deducir que:
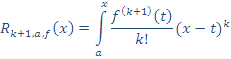
Es decir que se cumple para n = k + 1 y por tanto, queda demostrado que:
