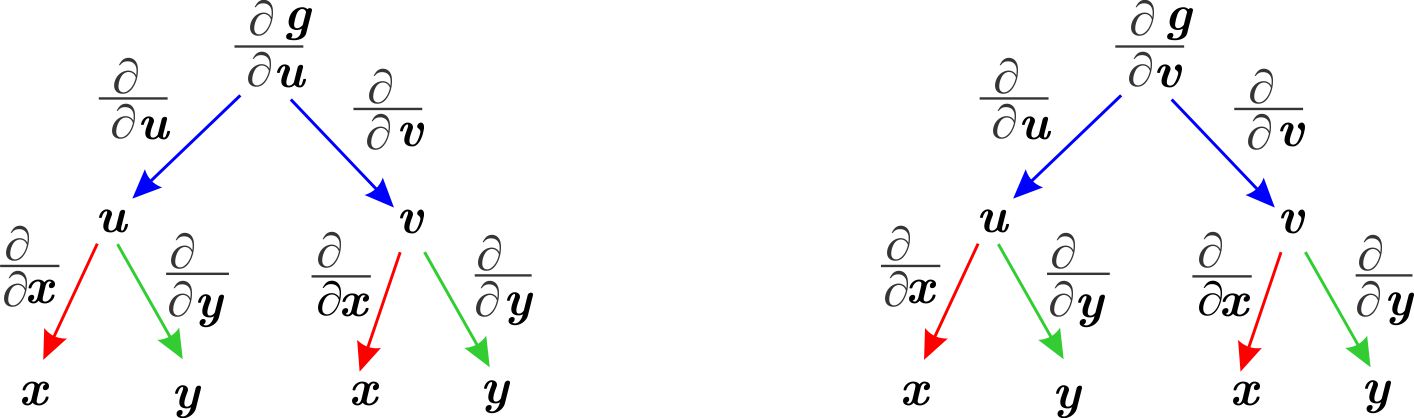Regla de la Cadena de Funciones de Varias Variables
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

 |
Regla de la Cadena de Funciones de Varias VariablesAngel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) |  |
Lema 1
Sea $T:\mathbb{R}^{n}\longrightarrow \mathbb{R}^{m}$ una función lineal
dada por la $m\times n$ matriz $A=\left( a_{ij}\right) .$ Tomamos
\begin{equation*}
\left\Vert A\right\Vert =\left( \sum_{i,j=1}^{n}a_{ij}^{2}\right) ^{\frac{1}{2}}=
\left( \sum_{i=1}^{m}\sum_{j=1}^{n}a_{ij}^{2}\right) ^{
\frac{1}{2}}=\left(\sum_{j=1}^{n}\sum_{i=1}^{m}a_{ij}^{2}\right) ^{\frac{1}{2}}.
\end{equation*}
Este número es mayor o igual que $0$ y es llamado la norma de $A.$
Utilizar la desigualdad de Cauchy-Schwarz para probar que
\begin{equation*}
\left\Vert A\overline{x}\right\Vert \leq \left\Vert A\right\Vert \left\Vert
\overline{x}\right\Vert .
\end{equation*}
Demostración:
\begin{equation*} T(\overline{x})=A\overline{x}=\left( \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \end{array} \right) \left( \begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array} \right) =\left( \begin{array}{c} \sum_{j=1}^{n}a_{1j}x_{j} \\ \vdots \\ \sum_{j=1}^{n}a_{mj}x_{j} \end{array} \right) =\left( \begin{array}{c} y_{1} \\ \vdots \\ y_{m} \end{array} \right) \end{equation*}
entonces
\begin{equation*} \left\Vert A\overline{x}\right\Vert =\sqrt{\sum_{i=1}^{m}\left( y_{i}\right) ^{2}} \end{equation*}
donde
\begin{equation*} y_{i}=\sum_{j=1}^{n}a_{ij}x_{j}=\left( a_{i1},\ldots ,a_{in}\right) \cdot \left( x_{1},\ldots ,x_{n}\right) . \end{equation*}
La desigualdad de Cauchy-Schwarz afirma que
\begin{equation*} \left\vert \overline{a}\cdot \overline{b}\right\vert \leq \left\Vert \overline{a}\right\Vert \left\Vert \overline{b}\right\Vert \end{equation*}
entonces
\begin{equation*} \left\vert \overline{a}\cdot \overline{b}\right\vert ^{2}\leq \left\Vert \overline{a}\right\Vert ^{2}\left\Vert \overline{b}\right\Vert ^{2}. \end{equation*}
Así
\begin{eqnarray*} y_{i}^{2} &=&\left( \left( a_{i1},\ldots ,a_{in}\right) \cdot \left( x_{1},\ldots ,x_{n}\right) \right) ^{2} \\ \\ &\leq &\left\Vert \overline{x}\right\Vert ^{2}\left\Vert \left( a_{i1},\ldots ,a_{in}\right) \right\Vert ^{2} \\ \\ &=&\left\Vert \overline{x}\right\Vert ^{2}\sum_{j=1}^{n}a_{ij}^{2}, \end{eqnarray*}
de donde
\begin{equation*} \left\Vert A\overline{x}\right\Vert \leq \sqrt{\sum_{i=1}^{m}\left \Vert \overline{x}\right\Vert ^{2}\sum_{j=1}^{n}a_{ij}^{2}}=\sqrt{ \left\Vert \overline{x}\right\Vert ^{2}\sum_{i=1}^{m}\sum_{j=1}^{n}a_{ij}^{2}}=\left\Vert \overline{x}\right\Vert \sqrt{\sum_{i=1}^{m}\sum _{j=1}^{n}a_{ij}^{2}}=\left\Vert A\right\Vert \left\Vert \overline{x} \right\Vert . \end{equation*}
Definición
Una función $f:U\subset \mathbb{R}^{n}\longrightarrow \mathbb{R}^{m},$
con U abierto, es derivable en $\overline{x}_{0}\in U,$ si existe una $
m\times n$ matriz $A$ que satisface
\begin{equation}
\lim_{\overline{x}\rightarrow \overline{x}_{0}}\dfrac{\left\Vert
f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) -A\left(
\overline{x}-\overline{x}_{0}\right) \right\Vert }{\left\Vert \overline{x}-
\overline{x}_{0}\right\Vert }=0. \label{limdef} \tag{1}
\end{equation}
Lo anterior equivale a que para cada $\varepsilon >0$ existe $\delta >0$ tal
que
\begin{equation}
\left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right)
-A\left( \overline{x}-\overline{x}_{0}\right) \right\Vert \leq \varepsilon
\left\Vert \overline{x}-\overline{x}_{0}\right\Vert \label{equiv} \tag{2}
\end{equation}
si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta .$
En tal caso $A$ es la matriz jacobiana $D_{f}\left( \overline{x}
_{0}\right) $ de $f$ evaluada en $\overline{x}_{0}$.
Teorema Auxiliar
Sea $f:U\subset \mathbb{R}^{n}\longrightarrow \mathbb{R}^{m},$ con U abierto, derivable en $\overline{x}_{0}\in U,$ entonces existen $M_{1}>0,$ $ \delta _{1}>0$ tales que \[\text{ si } \left\Vert \overline{x}-\overline{x} _{0}\right\Vert <\delta _{1} \text{ entonces } \left\Vert f\left( \overline{x} \right) -f\left( \overline{x}_{0}\right) \right\Vert \leq M_{1}\left\Vert \overline{x}-\overline{x}_{0}\right\Vert .\]
Demostración:
Sea $M=\left\Vert D_{f}\left( \overline{x}_{0}\right) \right\Vert $. Por el Lema 1
\begin{equation*} \left\Vert D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{ x}_{0}\right) \right\Vert \leq M\left\Vert \overline{x}-\overline{x} _{0}\right\Vert . \end{equation*}
Sea $\varepsilon =1,$ por (\ref{equiv}) existe $\delta _{1}>0$ tal que si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <$ $\delta _{1}$ entonces
\begin{equation*} \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \leq \left\Vert \overline{x}-\overline{x} _{0}\right\Vert . \end{equation*}
De donde si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta _{1} $ entonces
\begin{eqnarray*} \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right\Vert & = &\left\Vert f\left( \overline{x}\right) -f\left( \overline{x} _{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}- \overline{x}_{0}\right) +D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x}_{0}\right) \right\Vert \\ &\leq &\left\Vert f\left( \overline{x}\right) -f\left( \overline{x} _{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}- \overline{x}_{0}\right) \right\Vert +\left\Vert D_{f}\left( \overline{x} _{0}\right) \left( \overline{x}-\overline{x}_{0}\right) \right\Vert \\ &\leq &\left\Vert \overline{x}-\overline{x}_{0}\right\Vert +M\left\Vert \overline{x}-\overline{x}_{0}\right\Vert \\ & = &\left( M+1\right) \left\Vert \overline{x}-\overline{x}_{0}\right\Vert . \end{eqnarray*}
Tomando $M_{1}=M+1,$ entonces se cumple lo que queríamos.
Teorema Regla de la cadena
Sean $U\subset \mathbb{R}^{n}$ y $V\subset \mathbb{R}^{m}$ abiertos, $ f:U\subset \mathbb{R}^{n}\longrightarrow \mathbb{R}^{m}$, $g:V\subset \mathbb{R}^{m}\longrightarrow \mathbb{R}^{p}$ dos funciones tales que $ f(U)\subset V.$ Supongamos que $f$ es derivable en $\overline{x}_{0}\in U$ y $g$ es derivable en $\overline{y}_{0}=f\left( \overline{x}_{0}\right) .$ Entonces $g\circ f$ es derivable en $\overline{x}_{0}$ y \begin{equation*} D_{g\circ f}\left( \overline{x}_{0}\right) =D_{g}\left( \overline{y} _{0}\right) D_{f}\left( \overline{x}_{0}\right) . \end{equation*} El lado derecho de la igualdad es un producto de matrices.
Demostración:
\begin{equation*} \left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \leq \varepsilon \left\Vert \overline{x}-\overline{x} _{0}\right\Vert \end{equation*}
si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta .$
Primero escribimos el lado izquierdo como
\begin{eqnarray*} & & g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x} _{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x}_{0}\right) \\ & & \\ &=& g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x} _{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) +D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right)\end{eqnarray*}
de donde
\begin{eqnarray*} & &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \\ & & \\ &\leq &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert +\left\Vert D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{ x}-\overline{x}_{0}\right) \right\Vert \\ & & \\ & = &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert +\left\Vert D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) -D_{f}\left( \overline{x }_{0}\right) \left( \overline{x}-\overline{x}_{0}\right) \right) \right\Vert \\ & & \\ &\leq &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert +\left\Vert D_{g}\left( \overline{y}_{0}\right) \right\Vert \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert , \end{eqnarray*}
ya que por el Lema 1, se satisface
\begin{equation*} \left\Vert D_{g}\left( \overline{y}_{0}\right) \overline{h}\right\Vert \leq \left\Vert D_{g}\left( \overline{y}_{0}\right) \right\Vert \left\Vert \overline{h}\right\Vert \end{equation*}
Sea \(\left\Vert D_{g}\left( \overline{y}_{0}\right) \right\Vert < M.\) Entonces
\begin{eqnarray*} & &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \\ & & \\ &\leq &\left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert +M\left\Vert f\left( \overline{x}\right) -f\left( \overline{x} _{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}- \overline{x}_{0}\right) \right\Vert , \end{eqnarray*}
Como $f$ es derivable en $\overline{x}_{0},$ dado $\varepsilon >0$ existe $ \delta _{1}>0$ tal que si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta _{1}$, entonces
\begin{equation} \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \leq \dfrac{\varepsilon }{2M}\left\Vert \overline{x}- \overline{x}_{0}\right\Vert \label{desfder}\tag{3} \end{equation}
Por ser $f$ derivable, aplicando el Teorema Auxiliar, tenemos que existen $\delta _{2}>0$ y $M_{1}>0$ tales que si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta _{2}$ entonces
\begin{equation} \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right\Vert \leq M_{1}\left\Vert \overline{x}-\overline{x}_{0}\right\Vert . \label{desfM}\tag{4} \end{equation}
Por ser $g$ derivable en $\overline{y}_{0}$ existe $\delta _{3}>0$ tal que si $\left\Vert \overline{y}-\overline{y}_{0}\right\Vert <\delta _{3}$, entonces
\begin{equation} \left\Vert g\left( \overline{y}\right) -g\left( \overline{y}_{0}\right) -D_{g}\left( \overline{y}_{0}\right) \left( \overline{y}-\overline{y} _{0}\right) \right\Vert \leq \dfrac{\varepsilon \left\Vert \overline{y}- \overline{y}_{0}\right\Vert }{2M_{1}}. \label{desgM}\tag{5} \end{equation}
Tomemos $0<\delta <\min \left( \delta _{1},\delta _{2},\dfrac{\delta _{3}}{ M_{1}}\right) $ y $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta .$ Por (\ref{desfM})
\[ \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right\Vert \leq M_{1}\left\Vert \overline{x}-\overline{x}_{0}\right\Vert < M_{1}\delta < M_{1}\dfrac{\delta _{3}}{M_{1}}=\delta _{3}, \]
Como $\left\Vert f\left( \overline{x}\right) -f\left( \overline{x} _{0}\right) \right\Vert <\delta _{3}$ se sigue de (\ref{desgM}), con $ y=f\left( \overline{x}_{0}\right) $ y $y_{0}=f\left( \overline{x}_{0}\right) ,$ que se satisface
\begin{eqnarray*} \left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert &\leq &\dfrac{\varepsilon \left\Vert f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right\Vert }{2M_{1}} \\ &\leq &\dfrac{\varepsilon M_{1}\left\Vert \overline{x}-\overline{x} _{0}\right\Vert }{2M_{1}} \\ & = &\dfrac{\varepsilon \left\Vert \overline{x}-\overline{x}_{0}\right\Vert }{2}. \end{eqnarray*}
En resumen si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta ,$ entonces por esa última desigualdad y la desigualdad (\ref{desfder}) tenemos.
\begin{equation*} \left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) \left( f\left( \overline{x}\right) -f\left( \overline{x}_{0}\right) \right) \right\Vert +M\left\Vert f\left( \overline{x}\right) -f\left( \overline{x} _{0}\right) -D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}- \overline{x}_{0}\right) \right\Vert \end{equation*}
es menor que
\begin{equation*} \dfrac{\varepsilon \left\Vert \overline{x}-\overline{x}_{0}\right\Vert }{2}+ \dfrac{\varepsilon \left\Vert \overline{x}-\overline{x}_{0}\right\Vert }{2} \end{equation*}
y así, si $\left\Vert \overline{x}-\overline{x}_{0}\right\Vert <\delta $ entonces
\begin{equation*} \left\Vert g\left( f\left( \overline{x}\right) \right) -g\left( f\left( \overline{x}_{0}\right) \right) -D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) \left( \overline{x}-\overline{x} _{0}\right) \right\Vert \leq \left( \dfrac{\varepsilon }{2}+\dfrac{ \varepsilon }{2}\right) \left\Vert \overline{x}-\overline{x}_{0}\right\Vert =\varepsilon \left\Vert \overline{x}-\overline{x}_{0}\right\Vert . \end{equation*}
Queda probado que $g\circ f$ es derivable en $\overline{x}_{0}$ y $ D_{g\circ f}\left( \overline{x}_{0}\right) =D_{g}\left( \overline{y} _{0}\right) D_{f}\left( \overline{x}_{0}\right) ,$ donde $\overline{y} _{0}=f\left( \overline{x}_{0}\right) .$
Corolario
Supongamos que se satisfacen las hipótesis del teorema anterior con $
f\left( \overline{x}\right) =\left( f_{1}\left( \overline{x}\right)
,...,f_{m}\left( \overline{x}\right) \right) $ para $\overline{x}\in
\mathbb{R}^{n}$ y $g\left( \overline{y}\right) =\left( g_{1}\left(
\overline{y}\right) ,...,g_{p}\left( \overline{y}\right) \right) $ para $
\overline{y}\in \mathbb{R}^{m}.$ Entonces
\begin{eqnarray}
\dfrac{\partial \left( g_{i}\circ f\right) }{\partial x_{j}}\left( \overline{
x}_{0}\right) & = &\nabla g_{i}\left( f\left( \overline{x}_{0}\right) \right)
\cdot \dfrac{\partial f}{\partial x_{j}}\left( \overline{x}_{0}\right)
\label{DevPargral} \tag{6}\\
& = &\dfrac{\partial g_{i}}{\partial y_{1}}\left( f\left( \overline{x}
_{0}\right) \right) \dfrac{\partial f_{1}}{\partial x_{j}}\left( \overline{x}
_{0}\right) +\cdots +\dfrac{\partial g_{i}}{\partial y_{m}}\left( f\left(
\overline{x}_{0}\right) \right) \dfrac{\partial f_{m}}{\partial x_{j}}\left(
\overline{x}_{0}\right) \notag
\end{eqnarray}
para $1\leq i\leq p$ y $1\leq j\leq n$ donde
\begin{equation*}
\dfrac{\partial f}{\partial x_{j}}\left( \overline{x}_{0}\right) =\left(
\dfrac{\partial f_{1}}{\partial x_{j}}\left( \overline{x}_{0}\right) ,...,
\dfrac{\partial f_{m}}{\partial x_{j}}\left( \overline{x}_{0}\right) \right)
\end{equation*}
Demostración:
donde $\overline{y}_{0}=f\left( \overline{x}_{0}\right) .$
La matriz $D_{g\circ f}\left( \overline{x}_{0}\right) $ es de tamaño $ p\times n,$ en tanto que $D_{g}\left( \overline{y}_{0}\right) $ y $ D_{f}\left( \overline{x}_{0}\right) $ tienen tamaños $p\times m$ y $ m\times n,$ respectivamente.
Para $1\leq i\leq p$ el renglón $i$ de $D_{g\circ f}\left( \overline{x} _{0}\right) $ es $\nabla \left( g_{i}\circ f\right) \left( \overline{x} _{0}\right) ,$ por lo que su entrada $(i,j)$, con $1\leq j\leq n$, es $ \dfrac{\partial \left( g_{i}\circ f\right) }{\partial x_{j}}\left( \overline{ x}_{0}\right) .$
Por otra parte, la entrada $(i,j)$ de $D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) $ es el producto escalar del renglón $i$ de $D_{g}\left( \overline{y}_{0}\right) ,$ $\nabla g_{i}\left( f\left( \overline{x}_{0}\right) \right) ,$ por la columna $j$ de $D_{f}\left( \overline{x}_{0}\right) $, \begin{equation}\dfrac{\partial f}{\partial x_{j}}\left( \overline{x}_{0}\right) =\left( \dfrac{\partial f_{1}}{\partial x_{j}}\left( \overline{x}_{0}\right) ,...,\dfrac{\partial f_{m}}{\partial x_{j}}\left( \overline{x}_{0}\right) \right) , \end{equation} es decir \begin{equation}\nabla g_{i}\left( f\left( \overline{x}_{0}\right) \right) \cdot \dfrac{\partial f}{\partial x_{j}} \left( \overline{x}_{0}\right) . \end{equation}
Debido a la igualdad (\ref{reg2}), la entrada $\left( i,j\right) $ de $ D_{g\circ f}\left( \overline{x}_{0}\right) $ coincide con la de $D_{g}\left( \overline{y}_{0}\right) D_{f}\left( \overline{x}_{0}\right) ,$ con lo que obtenemos la igualdad (\ref{DevPargral}).
Dos casos particulares del corolario anterior son los que se tratan en los siguientes dos resultados en los que $g$ tiene una sola función componente, es decir es una función real.
Corolario 1
Sean $U\subset \mathbb{R}^{2}$ y $V\subset \mathbb{R}^{2}$ abiertos.
Supongamos que $f:U\subset \mathbb{R}^{2}\longrightarrow \mathbb{R}^{2}$ y $
g:V\subset \mathbb{R}^{2}\longrightarrow \mathbb{R}$ son derivables en sus
dominios. Si $f(U)\subset V$ y $f\left( x,y\right) =\left( u\left(
x,y\right) ,v\left( x,y\right) \right) $ , entonces la función
\begin{equation*}
h\left( x,y\right) =g\left( f\left( x,y\right) \right) =g\left( u\left(
x,y\right) ,v\left( x,y\right) \right)
\end{equation*}
es derivable en $U$ y para cada $\left( x,y\right) \in U$ se cumple:
\begin{eqnarray}
\dfrac{\partial h}{\partial x}\left( x,y\right) & = &\dfrac{\partial g}{
\partial u}\left( f\left( x,y\right) \right) \dfrac{\partial u}{\partial x}
\left( x,y\right) +\dfrac{\partial g}{\partial v}\left( f\left( x,y\right)
\right) \dfrac{\partial v}{\partial x}\left( x,y\right) \label{ForCor1}\tag{8} \\
& = &\nabla g\left( f\left( x,y\right) \right) \cdot \dfrac{\partial f}{
\partial x}\left( x,y\right) \notag \\
& & \notag \\
\dfrac{\partial h}{\partial y}\left( x,y\right) & = &\dfrac{\partial g}{
\partial u}\left( f\left( x,y\right) \right) \dfrac{\partial u}{\partial y}
\left( x,y\right) +\dfrac{\partial g}{\partial v}\left( f\left( x,y\right)
\right) \dfrac{\partial v}{\partial y}\left( x,y\right) \notag \\
& = &\nabla g\left( f\left( x,y\right) \right) \cdot \dfrac{\partial f}{
\partial y}\left( x,y\right) \notag
\end{eqnarray}
donde $\dfrac{\partial f}{\partial x}\left( x,y\right) =\left( \dfrac{
\partial u}{\partial x}\left( x,y\right) ,\dfrac{\partial v}{\partial x}
\left( x,y\right) \right) $ y $\dfrac{\partial f}{\partial y}\left(
x,y\right) =\left( \dfrac{\partial u}{\partial y}\left( x,y\right) ,\dfrac{
\partial v}{\partial y}\left( x,y\right) \right) .$
Demostración:
Si
\begin{equation*} h\left( x,y\right) =g\left( u\left( x,y\right) ,v\left( x,y\right) \right) \end{equation*}
entonces una variación en $x$ implica una variación en $u\left( x,y\right) $ y $v\left( x,y\right) $ lo que a su vez implica que $g$ varíe. Así, resulta natural que para calcular $\dfrac{\partial h}{ \partial x}$ debamos tomar en cuenta las parciales $\dfrac{\partial u}{ \partial x}$ y $\dfrac{\partial v}{\partial x}$ así como $\dfrac{ \partial g}{\partial u}$ y $\dfrac{\partial g}{\partial v}.$ La regla de la cadena nos dice cómo se relacionan todos estos valores.
Podemos considerar que $\dfrac{\partial g}{\partial u}\dfrac{\partial u}{ \partial x}$ nos da la variación de $h$ debido al cambio de $u$ por variar $x$; en tanto que, $\dfrac{\partial g}{\partial v}\dfrac{\partial v}{ \partial x}$ nos da la variación de $h$ debido al cambio de $v$ por variar $x.$ Y la suma de las dos nos da la medida de cómo cambia $h$ al variar $x;$ es decir \begin{equation*} \dfrac{\partial h}{\partial x}=\dfrac{\partial g}{\partial u}\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{\partial x}. \end{equation*}
Una discusión similar se puede hacer para $\dfrac{\partial h}{\partial y}.$
Para recordar la fórmula (\ref{ForCor1}) utilizamos el siguiente esquema
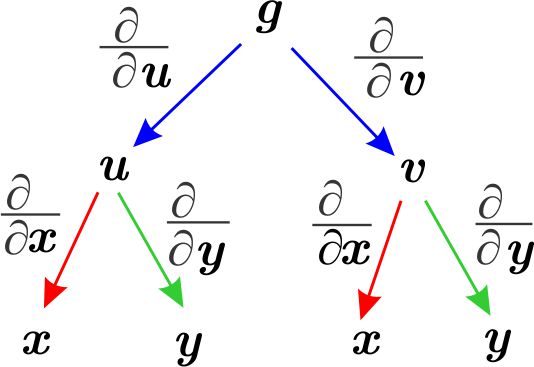
Observamos que, por ejemplo, para encontrar $\dfrac{\partial h}{\partial x},$ identificamos en la parte inferior, todos los símbolos $x.$ Seguimos desde $g$, los caminos que lleven a dichos símbolos, calculamos las derivadas indicadas siguiendo cada uno de los caminos multiplicando las derivadas obtenidas y sumamos el resultado de cada uno de ellos. Así, observamos que hay dos caminos que terminan en $x,$ en los que vemos
\begin{equation*} \dfrac{\partial g}{\partial u}\dfrac{\partial u}{\partial x}\qquad \qquad \text{y}\qquad \qquad \dfrac{\partial g}{\partial v}\dfrac{\partial v}{ \partial x} \end{equation*}
en el de la izquierda y derecha respectivamente. Entonces
\begin{equation*} \dfrac{\partial h}{\partial x}=\dfrac{\partial g}{\partial u}\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{\partial x}. \end{equation*}
Corolario 2
Sean $f:U\subset \mathbb{R}^{3}\longrightarrow \mathbb{R}^{3}$ una función derivable en un conjunto abierto $U,$ dada por
$f\left(x,y,z\right) =\left( u\left( x,y,z\right) ,v\left( x,y,z\right) ,w\left(
x,y,z\right) \right) $ y $g:V\subset \mathbb{R}^{3}\longrightarrow
\mathbb{R}$ una función derivable en su dominio. Si
\begin{equation*}
h\left( x,y,z\right) =g\left( f\left( x,y,z\right) \right) =g\left( u\left(
x,y,z\right) ,v\left( x,y,z\right) ,w\left( x,y,z\right) \right)
\end{equation*}
entonces
\begin{eqnarray*}
\dfrac{\partial h}{\partial x}\left( x,y,z\right) & = &\dfrac{\partial g}{
\partial u}\dfrac{\partial u}{\partial x}\left( x,y,z\right) +\dfrac{
\partial g}{\partial v}\dfrac{\partial v}{\partial x}\left( x,y,z\right) +
\dfrac{\partial g}{\partial w}\dfrac{\partial w}{\partial x}\left(
x,y,z\right) \\
& & \\
\dfrac{\partial h}{\partial y}\left( x,y,z\right) & = &\dfrac{\partial g}{
\partial u}\dfrac{\partial u}{\partial y}\left( x,y,z\right) +\dfrac{
\partial g}{\partial v}\dfrac{\partial v}{\partial y}\left( x,y,z\right) +
\dfrac{\partial g}{\partial w}\dfrac{\partial w}{\partial y}\left(
x,y,z\right) \\
& & \\
\dfrac{\partial h}{\partial z}\left( x,y,z\right) & = &\dfrac{\partial g}{
\partial u}\dfrac{\partial u}{\partial z}\left( x,y,z\right) +\dfrac{
\partial g}{\partial v}\dfrac{\partial v}{\partial z}\left( x,y,z\right) +
\dfrac{\partial g}{\partial w}\dfrac{\partial w}{\partial z}\left(
x,y,z\right)
\end{eqnarray*}
Donde las parciales de $g$ están evaluadas en $f\left( x,y,z\right)
=\left( u\left( x,y,z\right) ,v\left( x,y,z\right) ,w\left( x,y,z\right)
\right) .$
Demostración:
Para recordar esta fórmula utilizamos el siguiente esquema
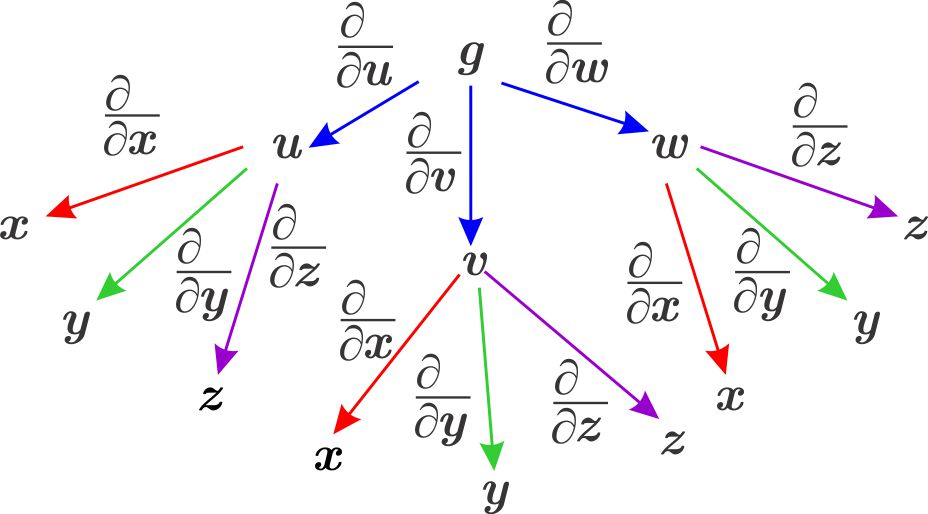
Ejemplo
Sea $h\left( x,y\right) =\left( x+y\right) \ \text{sen}\ \left( x^{2}+y^{3}\right) .$ Encuentra $\dfrac{\partial h}{\partial x}$ y $\dfrac{ \partial h}{\partial y}.$
Solución:
Observamos que $h\left( x,y\right) $ es el producto de las funciones $ f\left( x,y\right) =x+y$ y $g\left( x,y\right) =\ \text{sen}\ \left( x^{2}+y^{3}\right) ,$ donde a su vez $g$ es una composición de funciones.
Derivamos usando la fórmula del producto
\begin{eqnarray*} \dfrac{\partial h}{\partial x} & = &\dfrac{\partial }{\partial x}\left( \left( x+y\right) \ \text{sen}\ \left( x^{2}+y^{3}\right) \right) \\ & = &\left( \dfrac{\partial }{\partial x}\left( x+y\right) \right) \ \text{sen}\ \left( x^{2}+y^{3}\right) +\left( x+y\right) \left( \dfrac{\partial }{ \partial x}\ \text{sen}\ \left( x^{2}+y^{3}\right) \right) \\ & = &\ \text{sen}\ \left( x^{2}+y^{3}\right) +\left( x+y\right) \left( \dfrac{ \partial }{\partial x}\ \text{sen}\ \left( x^{2}+y^{3}\right) \right) \end{eqnarray*}
para calcular la derivada que falta usamos la regla de la cadena, de donde
\begin{equation*} \dfrac{\partial h}{\partial x}=\ \text{sen}\ \left( x^{2}+y^{3}\right) +\left( x+y\right) \left( \cos \left( x^{2}+y^{3}\right) \right) 2x. \end{equation*}
De la misma manera
\begin{eqnarray*} \dfrac{\partial h}{\partial y} & = &\dfrac{\partial }{\partial y}\left( \left( x+y\right) \ \text{sen}\ \left( x^{2}+y^{3}\right) \right) \\ & = &\left( \dfrac{\partial }{\partial y}\left( x+y\right) \right) \ \text{sen}\ \left( x^{2}+y^{3}\right) +\left( x+y\right) \left( \dfrac{\partial }{ \partial y}\ \text{sen}\ \left( x^{2}+y^{3}\right) \right) \\ & = &\ \text{sen}\ \left( x^{2}+y^{3}\right) +\left( x+y\right) \left( \cos \left( x^{2}+y^{3}\right) \right) 3y^{2}. \end{eqnarray*}
Observación:
Recordamos que si una función $f:U\subset \mathbb{R}^{n}\longrightarrow \mathbb{R}^{n}$ tiene derivadas parciales continuas en $U$, entonces $f$ es derivable en $U$. Así, cuando $f$ es de clase $C^{2},$ entonces ella y sus derivadas parciales son funciones derivables.
Corolario 3
Sean $f:U\subset \mathbb{R}^{2}\longrightarrow \mathbb{R}^{2}$ una
transformación de clase $C^{2}$ en el conjunto abierto $U$ dada por
$f\left( x,y\right) =\left( u\left( x,y\right) ,v\left(
x,y\right) \right) $ y $g:\mathbb{R}^{2}\longrightarrow \mathbb{R}$ una
función de clase $C^{2}$. Si
\begin{equation*}
h\left( x,y\right) =g\left( f\left( x,y\right) \right) =g\left( u\left(
x,y\right) ,v\left( x,y\right) \right)
\end{equation*}
entonces las derivadas de segundo orden de $h$ son
\begin{eqnarray*}
\dfrac{\partial ^{2}h}{\partial x^{2}} & = &\dfrac{\partial ^{2}g}{\partial
u^{2}}\left( \dfrac{\partial u}{\partial x}\right) ^{2}+\dfrac{\partial ^{2}g
}{\partial v\partial u}\dfrac{\partial v}{\partial x}\dfrac{\partial u}{
\partial x}+\dfrac{\partial g}{\partial u}\dfrac{\partial ^{2}u}{\partial
x^{2}}+\dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{
\partial x}\dfrac{\partial v}{\partial x}+\dfrac{\partial ^{2}g}{\partial
v^{2}}\left( \dfrac{\partial v}{\partial x}\right) ^{2}+\dfrac{\partial g}{
\partial v}\dfrac{\partial ^{2}v}{\partial x^{2}} \\
& & \\
\dfrac{\partial ^{2}h}{\partial y\partial x} & = &\dfrac{\partial ^{2}g}{
\partial u^{2}}\dfrac{\partial u}{\partial y}\dfrac{\partial u}{\partial x}+
\dfrac{\partial ^{2}g}{\partial v\partial u}\dfrac{\partial v}{\partial y}
\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial u}\dfrac{\partial
^{2}u}{\partial y\partial x}+\dfrac{\partial ^{2}g}{\partial u\partial v}
\dfrac{\partial u}{\partial y}\dfrac{\partial v}{\partial x}+\dfrac{\partial
^{2}g}{\partial v^{2}}\dfrac{\partial v}{\partial y}\dfrac{\partial v}{
\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial ^{2}v}{\partial
y\partial x} \\
& & \\
\dfrac{\partial ^{2}h}{\partial y^{2}} & = &\dfrac{\partial ^{2}g}{\partial
u^{2}}\left( \dfrac{\partial u}{\partial y}\right) ^{2}+\dfrac{\partial ^{2}g
}{\partial v\partial u}\dfrac{\partial v}{\partial y}\dfrac{\partial u}{
\partial y}+\dfrac{\partial g}{\partial u}\dfrac{\partial ^{2}u}{\partial
y^{2}}+\dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{
\partial y}\dfrac{\partial v}{\partial y}+\dfrac{\partial ^{2}g}{\partial
v^{2}}\left( \dfrac{\partial v}{\partial y}\right) ^{2}+\dfrac{\partial g}{
\partial v}\dfrac{\partial ^{2}v}{\partial y^{2}}
\end{eqnarray*}
Demostración:
\begin{equation*} \dfrac{\partial h}{\partial x}=\dfrac{\partial g}{\partial u}\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{\partial x} \quad \quad \quad \text{y}\quad \quad \quad \dfrac{\partial h}{\partial y}= \dfrac{\partial g}{\partial u}\dfrac{\partial u}{\partial y}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{\partial y} \end{equation*}
entonces
\begin{eqnarray} \dfrac{\partial }{\partial x}\left( \dfrac{\partial h}{\partial x}\right) & = & \dfrac{\partial }{\partial x}\left( \dfrac{\partial g}{\partial u}\dfrac{ \partial u}{\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{ \partial x}\right) \label{cadena1}\tag{9} \\ & = &\dfrac{\partial }{\partial x}\left( \dfrac{\partial g}{\partial u}\dfrac{ \partial u}{\partial x}\right) +\dfrac{\partial }{\partial x}\left( \dfrac{ \partial g}{\partial v}\dfrac{\partial u}{\partial x}\right) \quad \quad \quad \text{derivada de una suma} \notag \\ & = &\dfrac{\partial }{\partial x}\left( \dfrac{\partial g}{\partial u}\right) \dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial u}\dfrac{\partial }{\partial x}\left( \dfrac{\partial u}{\partial x}\right) +\dfrac{\partial }{ \partial x}\left( \dfrac{\partial g}{\partial v}\right) \dfrac{\partial u}{ \partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial }{\partial x} \left( \dfrac{\partial u}{\partial x}\right) \quad \quad \quad \text{ derivada de un producto} \notag \end{eqnarray}
Observamos que $\dfrac{\partial g}{\partial u}$ y $\dfrac{\partial g}{ \partial v}$ son funciones de $u$ y $v$ que a su vez dependen de $x$ y $y$ por lo que para calcular sus derivadas, con respecto a estas variables, debemos usar nuevamente la regla de la cadena (Ver Ejemplo)
Por lo tanto,
\begin{eqnarray} \dfrac{\partial ^{2}h}{\partial x^{2}} & = &\dfrac{\partial u}{\partial x} \left( \dfrac{\partial ^{2}g}{\partial u^{2}}\dfrac{\partial u}{\partial x}+ \dfrac{\partial ^{2}g}{\partial v\partial u}\dfrac{\partial v}{\partial x} \right) +\dfrac{\partial g}{\partial u}\dfrac{\partial ^{2}u}{\partial x^{2}} +\dfrac{\partial v}{\partial x}\left( \dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{\partial x}+\dfrac{\partial ^{2}g}{\partial v^{2}}\dfrac{\partial v}{\partial x}\right) +\dfrac{\partial g}{\partial v} \dfrac{\partial ^{2}v}{\partial x^{2}} \notag \\ & = &\dfrac{\partial ^{2}g}{\partial u^{2}}\left( \dfrac{\partial u}{\partial x }\right) ^{2}+\dfrac{\partial ^{2}g}{\partial v\partial u}\dfrac{\partial v}{ \partial x}\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial u} \dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{\partial x}\dfrac{\partial v}{\partial x}+ \dfrac{\partial ^{2}g}{\partial v^{2}}\left( \dfrac{\partial v}{\partial x} \right) ^{2}+\dfrac{\partial g}{\partial v}\dfrac{\partial ^{2}v}{\partial x^{2}} \notag \end{eqnarray}
Veamos el caso de la derivada mixta.
\begin{eqnarray*} \dfrac{\partial }{\partial y}\left( \dfrac{\partial h}{\partial x}\right) & = & \dfrac{\partial }{\partial y}\left( \dfrac{\partial g}{\partial u}\dfrac{ \partial u}{\partial x}+\dfrac{\partial g}{\partial v}\dfrac{\partial v}{ \partial x}\right) \\ & = &\dfrac{\partial u}{\partial x}\dfrac{\partial }{\partial y}\left( \dfrac{ \partial g}{\partial u}\right) +\dfrac{\partial g}{\partial u}\dfrac{ \partial }{\partial y}\left( \dfrac{\partial u}{\partial x}\right) +\dfrac{ \partial v}{\partial x}\dfrac{\partial }{\partial y}\left( \dfrac{\partial g }{\partial v}\right) +\dfrac{\partial g}{\partial v}\dfrac{\partial }{ \partial y}\left( \dfrac{\partial v}{\partial x}\right) \\ & = &\dfrac{\partial u}{\partial x}\left( \dfrac{\partial ^{2}g}{\partial u^{2} }\dfrac{\partial u}{\partial y}+\dfrac{\partial ^{2}g}{\partial v\partial u} \dfrac{\partial v}{\partial y}\right) +\dfrac{\partial g}{\partial u}\dfrac{ \partial ^{2}u}{\partial y\partial x}+\dfrac{\partial v}{\partial x}\left( \dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{\partial y}+ \dfrac{\partial ^{2}g}{\partial v^{2}}\dfrac{\partial v}{\partial y}\right) + \dfrac{\partial g}{\partial v}\dfrac{\partial ^{2}v}{\partial y\partial x} \\ & = &\dfrac{\partial ^{2}g}{\partial u^{2}}\dfrac{\partial u}{\partial y} \dfrac{\partial u}{\partial x}+\dfrac{\partial ^{2}g}{\partial v\partial u} \dfrac{\partial v}{\partial y}\dfrac{\partial u}{\partial x}+\dfrac{\partial g}{\partial u}\dfrac{\partial ^{2}u}{\partial y\partial x}+\dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{\partial u}{\partial y}\dfrac{\partial v}{ \partial x}+\dfrac{\partial ^{2}g}{\partial v^{2}}\dfrac{\partial v}{ \partial y}\dfrac{\partial v}{\partial x}+\dfrac{\partial g}{\partial v} \dfrac{\partial ^{2}v}{\partial y\partial x} \end{eqnarray*}
Por lo tanto,
\begin{equation*} \dfrac{\partial ^{2}h}{\partial y\partial x}=\dfrac{\partial ^{2}g}{\partial u^{2}}\dfrac{\partial u}{\partial y}\dfrac{\partial u}{\partial x}+\dfrac{ \partial ^{2}g}{\partial v\partial u}\dfrac{\partial v}{\partial y}\dfrac{ \partial u}{\partial x}+\dfrac{\partial g}{\partial u}\dfrac{\partial ^{2}u}{ \partial y\partial x}+\dfrac{\partial ^{2}g}{\partial u\partial v}\dfrac{ \partial u}{\partial y}\dfrac{\partial v}{\partial x}+\dfrac{\partial ^{2}g}{ \partial v^{2}}\dfrac{\partial v}{\partial y}\dfrac{\partial v}{\partial x}+ \dfrac{\partial g}{\partial v}\dfrac{\partial ^{2}v}{\partial y\partial x} \end{equation*}
Para recordar las fórmulas anteriores observamos, por ejemplo, que en el segundo renglón de (\ref{cadena1}) aparecen $\dfrac{\partial }{\partial x }\left( \dfrac{\partial g}{\partial u}\right) $ y $\dfrac{\partial }{ \partial x}\left( \dfrac{\partial g}{\partial v}\right) ,$ las cuales podemos calcular con el uso del esquema siguiente