Regla de la Cadena de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Si \(z=f\left( x,y\right) \) es una función real de clase \(C^{2}\) en \(\mathbb{R}^{2}.\) Calcula \(\dfrac{\partial ^{2}z}{\partial r^{2}},\) \( \dfrac{\partial ^{2}z}{\partial \theta \partial r},\) \(\dfrac{\partial ^{2}z}{ \partial \theta ^{2}} \) si \(x=r\cos \theta ,\) \(y=r\ \text{sen}\ \theta .\)

Solución:

Observamos el siguiente diagrama

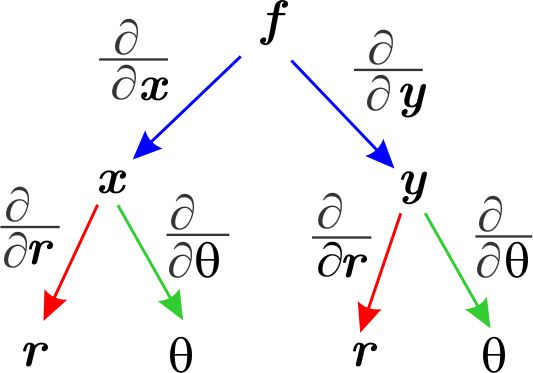
Calculamos

\begin{eqnarray*} \dfrac{\partial z}{\partial r} & = &\dfrac{\partial f}{\partial x}\dfrac{ \partial x}{\partial r}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{ \partial r} \\ & = &\dfrac{\partial f}{\partial x}\cos \theta +\dfrac{\partial f}{\partial y} \ \text{sen}\ \theta \\ & = &\cos \theta \dfrac{\partial f}{\partial x}+\ \text{sen}\ \theta \dfrac{ \partial f}{\partial y} \end{eqnarray*}

y

\begin{eqnarray*} \dfrac{\partial z}{\partial \theta } & = &\dfrac{\partial f}{\partial x}\dfrac{ \partial x}{\partial \theta }+\dfrac{\partial f}{\partial y}\dfrac{\partial y }{\partial \theta } \\ & = &\dfrac{\partial f}{\partial x}\left( -r\ \text{sen}\ \theta \right) + \dfrac{\partial f}{\partial y}\left( r\cos \theta \right) \\ & = &-r\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}+r\cos \theta \dfrac{ \partial f}{\partial y} \end{eqnarray*}

Ahora consideramos el siguiente diagrama

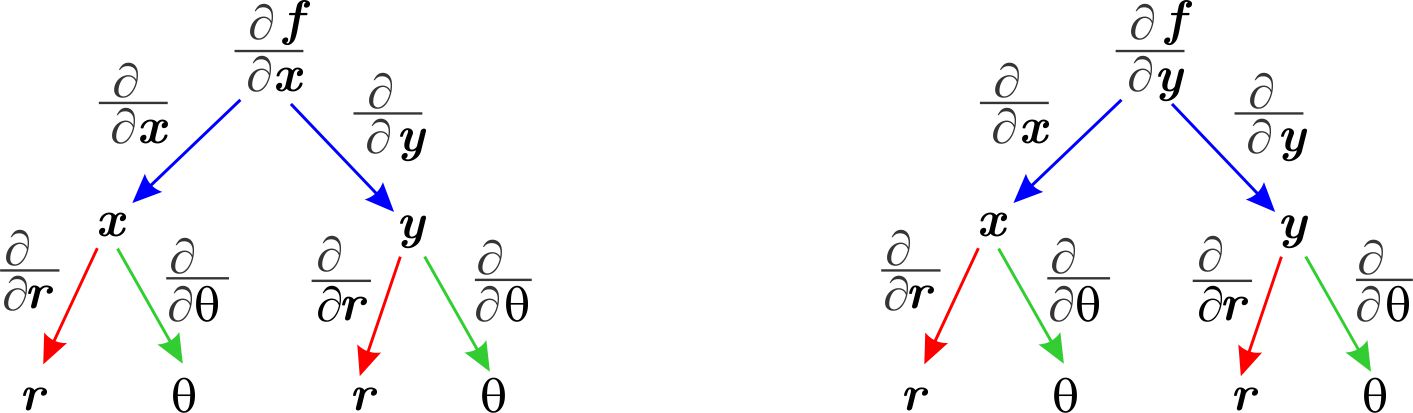
Calculamos

\begin{eqnarray*} \dfrac{\partial ^{2}z}{\partial r^{2}} & = &\dfrac{\partial }{\partial r} \left( \dfrac{\partial z}{\partial r}\right) \\ & = &\dfrac{\partial }{\partial r}\left( \cos \theta \dfrac{\partial f}{ \partial x}+\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}\right) \\ & = &\dfrac{\partial }{\partial r}\left( \cos \theta \right) \dfrac{\partial f }{\partial x}+\cos \theta \dfrac{\partial }{\partial r}\left( \dfrac{ \partial f}{\partial x}\right) +\dfrac{\partial }{\partial r}\left( \ \text{sen}\ \theta \right) \dfrac{\partial f}{\partial y}+\ \text{sen}\ \theta \dfrac{ \partial }{\partial r}\left( \dfrac{\partial f}{\partial y}\right) \\ & = &0+\cos \theta \left( \dfrac{\partial }{\partial x}\left( \dfrac{\partial f }{\partial x}\right) \dfrac{\partial x}{\partial r}+\dfrac{\partial }{ \partial y}\left( \dfrac{\partial f}{\partial x}\right) \dfrac{\partial y}{ \partial r}\right) +0+\ \text{sen}\ \theta \left( \dfrac{\partial }{\partial x }\left( \dfrac{\partial f}{\partial y}\right) \dfrac{\partial x}{\partial r}+ \dfrac{\partial }{\partial y}\left( \dfrac{\partial f}{\partial y}\right) \dfrac{\partial y}{\partial r}\right) \\ & = &\cos \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\dfrac{\partial x }{\partial r}+\dfrac{\partial ^{2}f}{\partial y\partial x}\dfrac{\partial y}{ \partial r}\right) +\ \text{sen}\ \theta \left( \dfrac{\partial ^{2}f}{ \partial x\partial y}\dfrac{\partial x}{\partial r}+\dfrac{\partial ^{2}f}{ \partial y^{2}}\dfrac{\partial y}{\partial r}\right) \\ & = &\cos \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\cos \theta + \dfrac{\partial ^{2}f}{\partial y\partial x}\ \text{sen}\ \theta \right) + \ \text{sen}\ \theta \left( \dfrac{\partial ^{2}f}{\partial x\partial y}\cos \theta +\dfrac{\partial ^{2}f}{\partial y^{2}}\ \text{sen}\ \theta \right) \\ & = &\cos ^{2}\theta \dfrac{\partial ^{2}f}{\partial x^{2}}+\cos \theta \ \text{sen}\ \theta \dfrac{\partial ^{2}f}{\partial y\partial x}+\cos \theta \ \text{sen}\ \theta \dfrac{\partial ^{2}f}{\partial x\partial y}+\ \text{sen}^{2} \theta \dfrac{\partial ^{2}f}{\partial y^{2}} \\ & = &\cos ^{2}\theta \dfrac{\partial ^{2}f}{\partial x^{2}}+2\cos \theta \ \text{sen}\ \theta \dfrac{\partial ^{2}f}{\partial y\partial x}+\ \text{sen}^{2} \theta \dfrac{\partial ^{2}f}{\partial y^{2}} \end{eqnarray*}

Calculamos la derivada mixta

\begin{eqnarray*} \dfrac{\partial ^{2}z}{\partial \theta \partial r} & = &\dfrac{\partial }{ \partial \theta }\left( \dfrac{\partial z}{\partial r}\right) \\ & = &\dfrac{\partial }{\partial \theta }\left( \cos \theta \dfrac{\partial f}{ \partial x}+\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}\right) \\ & = &\dfrac{\partial }{\partial \theta }\left( \cos \theta \right) \dfrac{ \partial f}{\partial x}+\cos \theta \dfrac{\partial }{\partial \theta } \left( \dfrac{\partial f}{\partial x}\right) +\dfrac{\partial }{\partial \theta }\left( \ \text{sen}\ \theta \right) \dfrac{\partial f}{\partial y}+ \ \text{sen}\ \theta \dfrac{\partial }{\partial \theta }\left( \dfrac{ \partial f}{\partial y}\right) \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}+\cos \theta \left( \dfrac{\partial }{\partial x}\left( \dfrac{\partial f}{\partial x}\right) \dfrac{\partial x}{\partial \theta }+\dfrac{\partial }{\partial y}\left( \dfrac{\partial f}{\partial x}\right) \dfrac{\partial y}{\partial \theta } \right) +\cos \theta \dfrac{\partial f}{\partial y}+\ \text{sen}\ \theta \left( \dfrac{\partial }{\partial x}\left( \dfrac{\partial f}{\partial y} \right) \dfrac{\partial x}{\partial \theta }+\dfrac{\partial }{\partial y} \left( \dfrac{\partial f}{\partial y}\right) \dfrac{\partial y}{\partial \theta }\right) \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}+\cos \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\dfrac{\partial x}{\partial \theta }+ \dfrac{\partial ^{2}f}{\partial y\partial x}\dfrac{\partial y}{\partial \theta }\right) +\cos \theta \dfrac{\partial f}{\partial y}+\ \text{sen}\ \theta \left( \dfrac{\partial ^{2}f}{\partial x\partial y}\dfrac{\partial x}{ \partial \theta }+\dfrac{\partial ^{2}f}{\partial y^{2}}\dfrac{\partial y}{ \partial \theta }\right) \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}+\cos \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -r\ \text{sen}\ \theta \right) + \dfrac{\partial ^{2}f}{\partial y\partial x}r\cos \theta \right) +\cos \theta \dfrac{\partial f}{\partial y}+\ \text{sen}\ \theta \left( \dfrac{ \partial ^{2}f}{\partial x\partial y}\left( -r\ \text{sen}\ \theta \right) + \dfrac{\partial ^{2}f}{\partial y^{2}}r\cos \theta \right) \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial x^{2}}+r\cos ^{2}\theta \dfrac{ \partial ^{2}f}{\partial y\partial x}+\cos \theta \dfrac{\partial f}{ \partial y}-r\ \text{sen} ^{2}\theta \dfrac{\partial ^{2}f}{ \partial x\partial y}+r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f }{\partial y^{2}} \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial x^{2}}+\left( r\cos ^{2}\theta -r \ \text{sen} ^{2}\theta \right) \dfrac{\partial ^{2}f}{\partial y\partial x}+\cos \theta \dfrac{\partial f}{\partial y}+r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial y^{2}} \\ & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial x^{2}}+r\cos 2\theta \dfrac{ \partial ^{2}f}{\partial y\partial x}+\cos \theta \dfrac{\partial f}{ \partial y}+r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial y^{2}} \end{eqnarray*}

y finalmente calculamos

\begin{eqnarray*} \dfrac{\partial ^{2}z}{\partial \theta ^{2}} & = &\dfrac{\partial }{\partial \theta }\left( \dfrac{\partial z}{\partial \theta }\right) \\ & = &\dfrac{\partial }{\partial \theta }\left( -r\ \text{sen}\ \theta \dfrac{ \partial f}{\partial x}+r\cos \theta \dfrac{\partial f}{\partial y}\right) \\ & = &\dfrac{\partial }{\partial \theta }\left( -r\ \text{sen}\ \theta \right) \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \dfrac{\partial }{ \partial \theta }\left( \dfrac{\partial f}{\partial x}\right) +\dfrac{ \partial }{\partial \theta }\left( r\cos \theta \right) \dfrac{\partial f}{ \partial y}+r\cos \theta \dfrac{\partial }{\partial \theta }\left( \dfrac{ \partial f}{\partial y}\right) \\ & = &-r\cos \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \left( \dfrac{\partial }{\partial x}\left( \dfrac{\partial f}{\partial x}\right) \dfrac{\partial x}{\partial \theta }+\dfrac{\partial }{\partial y}\left( \dfrac{\partial f}{\partial x}\right) \dfrac{\partial y}{\partial \theta } \right) -r\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}+r\cos \theta \left( \dfrac{\partial }{\partial x}\left( \dfrac{\partial f}{\partial y} \right) \dfrac{\partial x}{\partial \theta }+\dfrac{\partial }{\partial y} \left( \dfrac{\partial f}{\partial y}\right) \dfrac{\partial y}{\partial \theta }\right) \\ & = &-r\cos \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\dfrac{\partial x}{\partial \theta }+ \dfrac{\partial ^{2}f}{\partial y\partial x}\dfrac{\partial y}{\partial \theta }\right) -r\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}+r\cos \theta \left( \dfrac{\partial ^{2}f}{\partial x\partial y}\dfrac{\partial x}{ \partial \theta }+\dfrac{\partial ^{2}f}{\partial y^{2}}\dfrac{\partial y}{ \partial \theta }\right) \\ & = &-r\cos \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \left( \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -r\ \text{sen}\ \theta \right) + \dfrac{\partial ^{2}f}{\partial y\partial x}r\cos \theta \right) -r\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}+r\cos \theta \left( \dfrac{ \partial ^{2}f}{\partial x\partial y}\left( -r\ \text{sen}\ \theta \right) + \dfrac{\partial ^{2}f}{\partial y^{2}}r\cos \theta \right) \\ & = &-r\cos \theta \dfrac{\partial f}{\partial x}+r^{2}\ \text{sen}\ ^{2}\theta \dfrac{\partial ^{2}f}{\partial x^{2}}-r^{2}\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial y\partial x}-r\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}-r^{2}\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial x\partial y}+r^{2}\cos ^{2}\theta \dfrac{ \partial ^{2}f}{\partial y^{2}} \\ & = &-r\cos \theta \dfrac{\partial f}{\partial x}+r^{2}\ \text{sen} ^{2}\theta \dfrac{\partial ^{2}f}{\partial x^{2}}-2r^{2}\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial y\partial x}-r\ \text{sen}\ \theta \dfrac{\partial f}{\partial y}+r^{2}\cos ^{2}\theta \dfrac{ \partial ^{2}f}{\partial y^{2}} \end{eqnarray*}

En resumen

\begin{eqnarray*} \dfrac{\partial ^{2}z}{\partial r^{2}} & = &\cos ^{2}\theta \dfrac{\partial ^{2}f}{\partial x^{2}}+2\cos \theta \ \text{sen}\ \theta \dfrac{\partial ^{2}f }{\partial y\partial x}+\ \text{sen} ^{2}\theta \dfrac{\partial ^{2}f}{\partial y^{2}} \\ \dfrac{\partial ^{2}z}{\partial \theta \partial r} & = &-\ \text{sen}\ \theta \dfrac{\partial f}{\partial x}-r\ \text{sen}\ \theta \cos \theta \dfrac{ \partial ^{2}f}{\partial x^{2}}+r\cos 2\theta \dfrac{\partial ^{2}f}{ \partial y\partial x}+\cos \theta \dfrac{\partial f}{\partial y}+r\ \text{sen}\ \theta \cos \theta \dfrac{\partial ^{2}f}{\partial y^{2}} \\ \dfrac{\partial ^{2}z}{\partial \theta ^{2}} & = &-r\cos \theta \dfrac{ \partial f}{\partial x}+r^{2}\ \text{sen}\ ^{2}\theta \dfrac{ \partial ^{2}f}{\partial x^{2}}-2r^{2}\ \text{sen}\ \theta \cos \theta \dfrac{ \partial ^{2}f}{\partial y\partial x}-r\ \text{sen}\ \theta \dfrac{\partial f }{\partial y}+r^{2}\cos ^{2}\theta \dfrac{\partial ^{2}f}{\partial y^{2}} \end{eqnarray*}