Coordenadas Polares

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Espirales

Las espirales son curvas que se enrollan un número infinito de veces alrededor de un punto, de tal manera que en sus puntos la coordenada polar \)r>0\) aumenta o disminuye a medida que \(\theta >0\) aumenta.

Espiral de Arquímedes

Ésta es una de las más conocidas y tiene por ecuación alguna de las formas siguientes: \begin{equation*} r=a\theta ,\qquad \theta \geq 0,\qquad a>0\qquad \text{o bien}\qquad r=-a\theta ,\qquad \theta \geq 0,\qquad a>0. \end{equation*} Observa que estas curvas pasan por el origen y los criterios de simetría no dan información alguna.

Dibujemos la gráfica de \(r=a\theta ,\qquad \theta \geq 0,\qquad a>0.\)

En el plano cartesiano \(\Theta R\):

Así, \(r\) crece a medida que \(\theta \) se incrementa, la gráfica de \( r=a\theta \) en el plano \(XY\) es:

Espiral logarítmica

La ecuación polar de una espiral logarítmica es: \begin{equation*} \log _{b}r=\log _{b}a+k\theta ,\qquad a>0,\qquad b>0 \end{equation*} donde \(\log _{b}r\) indica logaritmo base \(b\) de \(r.\)

Consideramos la ecuación \begin{equation*} \log _{b}r=\log _{b}a+k\theta , \end{equation*} aplicamos de ambos lados la función \(b^{x},\) entonces \begin{equation*} b^{\log _{b}r}=b^{\log _{b}a+k\theta } \end{equation*} puesto que las funciones \begin{equation*} y=b^{x}\qquad \text{y}\qquad x= \log _{b}y \end{equation*} son inversas, tenemos \begin{eqnarray*} r & = & b^{\log _{b}a+k\theta } \\ & = & b^{\log _{b}a}b^{k\theta } \\ & = & ab^{k\theta }. \end{eqnarray*} Es decir, la ecuación \(\log _{b}r=\log _{b}a+k\theta ,\) correspondiente a una espiral logarítmica, es equivalente a \(r=ab^{k\theta }.\)

Ejemplo

Dibuja la gráfica de la espiral logarítmica dada por la ecuación \(r=e^{\theta }.\)
Solución:
En el plano cartesiano \(\Theta R\):

Observemos que esta curva no corta el eje \(\Theta ,\) entonces en el plano cartesiano \(\Theta R\) la curva nunca toca el origen, además es estrictamente creciente, por lo cual se obtiene una espiral cuando dibujamos su gráfica polar.
La gráfica polar de \(r=e^{\theta }\) es

La espiral \(r=e^{\theta }\) que dibujamos, corresponde al caso \(a=1, \ b=e, \ k=1.\)

Espiral parábolica

La espiral parábolica está dada por la ecuación polar: \begin{equation*} r^{2}=a\theta \qquad a,\theta >0 \end{equation*}

Ejemplos

Dibuja la gráfica de la espiral parabólica dada por la ecuación \(r^{2}=\theta ,r>0.\)
Solución:
Analicemos esta curva. Al igual que en la espiral de Arquímedes, los criterios de simetría no nos dan información.

la gráfica polar es:
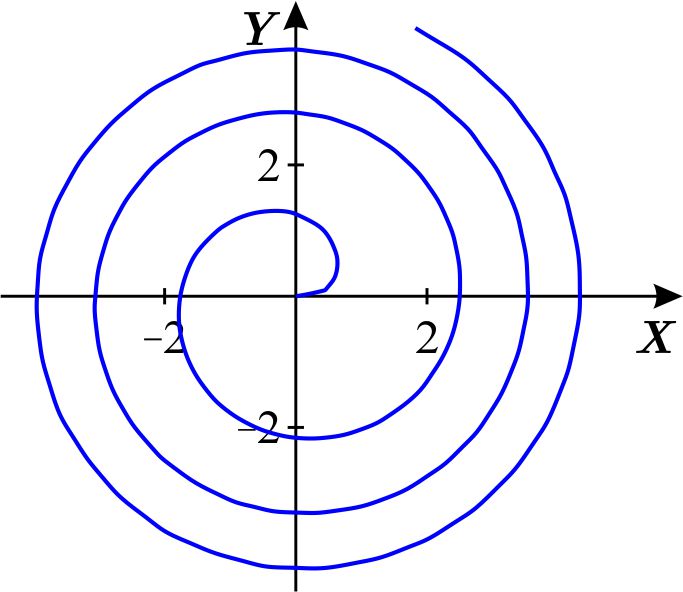
Dibuja la gráfica de la espiral parabólica dada por la ecuación \(r^{2}=\theta ,r < 0\).
Solución:
Dibujamos la gráfica de \(r^{2}=\theta ,r < 0\) en el plano cartesiano \( \Theta R\):
la gráfica polar es:

En lo que sigue, veremos dos curvas que son muy parecidas en el plano cartesiano \(\Theta R\) aunque no lo son en el plano polar.

Lituus

La espiral dada por la ecuación polar: \begin{equation*} r^{2}=\dfrac{a}{\theta }\qquad a,\theta >0 \end{equation*} se conoce con el nombre de lituus (trompeta)

Ejemplo

Dibuja la gráfica de la espiral dada por la ecuación \(r^{2}= \dfrac{1}{\theta },r>0.\)
Solución:
La gráfica en el plano cartesiano \(\Theta R\) de \(r^{2}=\dfrac{1}{\theta } ,r>0\) es:

la gráfica en el plano polar es:

Espiral hiperbólica

La espiral hiperbólica está dada por la ecuación: \begin{equation*} r=\dfrac{a}{\theta } \end{equation*}

Ejemplo

Dibuja la gráfica de la espiral hiperbólica dada por la ecuación \(r=\dfrac{1}{\theta }, \ \theta >0.\)
Solución:
En el plano cartesiano \(\Theta R\):

la gráfica polar es:

Observamos que para la espiral hiperbólica \(r=\dfrac{1}{\theta },\) la ordenada cartesiana de cada uno de sus puntos es de la forma \(y=r\ \text{sen} \ \theta =\dfrac{1}{\theta }\ \text{sen} \ \theta .\) Cuando \(\theta \) se aproxima a cero, tenemos: \begin{equation*} \lim\limits_{\theta \rightarrow 0}\dfrac{\ \text{sen} \ \theta }{\theta }=1, \end{equation*} es decir, cuando \(\theta \) se acerca a cero, la ordenada cartesiana \(y\) se acerca a \(1\) y por consiguiente, la gráfica polar de \(r=\dfrac{1}{\theta }\) se aproxima a la recta \(y=1.\)
En cambio, para la espiral hiperbólica \(r^{2}=\dfrac{1}{\theta },\) \(r>0,\) \(\theta >0\), tenemos que como: \begin{equation*} r=\dfrac{1}{\sqrt{\theta }} \end{equation*} entonces \begin{equation*} y=\dfrac{1}{\sqrt{\theta }}\ \text{sen} \ \theta \end{equation*} y \begin{eqnarray*} \lim\limits_{\theta \rightarrow 0}\dfrac{\ \text{sen} \ \theta }{\sqrt{\theta } } & = & \lim\limits_{\theta \rightarrow 0}\dfrac{\cos \theta }{\dfrac{1}{2\sqrt{ \theta }}} \\ & = & \lim\limits_{\theta \rightarrow 0}2\sqrt{\theta }\cos \theta \\ & = & 0. \end{eqnarray*} Resumiendo, no obstante que las curvas \(r=\dfrac{1}{\theta }\) y \(r=\dfrac{1}{ \sqrt{\theta }}\) en el plano cartesiano \(\Theta R\) son parecidas, sus gráficas polares tienen diferencias más marcadas, que se deben a qué tan rápido crece o decrece la función en cada caso.

Ejercicios

Dibuja las gráficas de las siguientes ecuaciones.

\(r=2\theta \qquad \theta \geq 0.\)
\(r=3\theta \qquad \theta \leq 0.\)
\(r=3e^{\theta }.\)
\(r=5\left( 3^{\theta }\right) .\)
\(r=2^{3\theta }.\)
\(r=2e^{-2\theta }.\)
\(r=\dfrac{2}{\theta }, \qquad \theta < 0.\)
\(r=\dfrac{3}{\theta }, \qquad \theta >0.\)
\(r^{2}=4\theta, \qquad r>0.\)
\(r^{2}=\dfrac{3}{\theta }, \qquad r < 0.\)

Universidad Nacional Autónoma de México