Coordenadas Polares Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ecuaciones Polares

De la misma manera que los puntos tienen asociadas coordenadas polares y cartesianas, una curva tiene asociada una ecuación polar y una cartesiana, el paso de una a otra se logra mediante el uso de las ecuaciones \begin{equation} x^{2}+y^{2}=r^{2},\qquad \text{sen}\ \theta =\dfrac{y}{\sqrt{x^{2}+y^{2}}} ,\qquad \cos \theta =\dfrac{x}{\sqrt{x^{2}+y^{2}}},\qquad x=r\cos \theta ,\qquad y=r\ \text{sen}\ \theta \label{I} \tag{2} \end{equation}

Recordamos que en el sistema de coordenadas polares se usa una semirrecta llamada eje polar, cuyo extremo inicial \(O\) es llamado polo. Cuando sobrepongamos los sistemas polar y cartesiano, siempre consideraremos que el eje polar coincide con el semieje positivo \(X\) del sistema cartesiano y que el polo está en el origen del sistema \(XY.\)

Ejemplos

1. Encuentra la ecuación cartesiana de la curva cuya ecuación en coordenadas polares es \begin{equation*} r=\dfrac{4}{1-\cos \theta } \end{equation*} Solución:

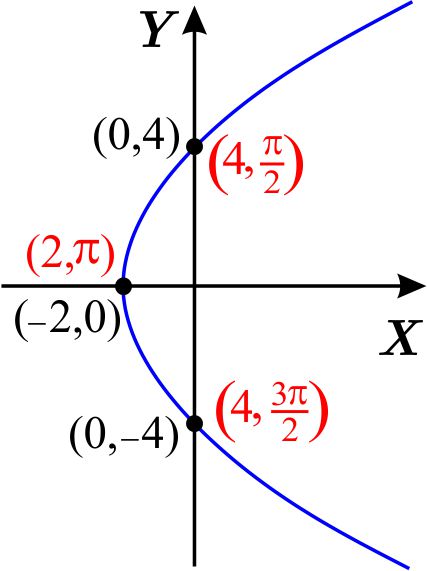
   En la figura, vemos la gráfica polar de la curva. Para los puntos marcados sobre la curva, vemos en color negro las coordenadas cartesianas y en rojo las polares, correspondientes.

   Utilizando las ecuaciones (\ref{I}), obtenemos la ecuación cartesiana de la curva: \begin{eqnarray*} r\left( 1-\cos \theta \right) & = & 4 \\ r-r\cos \theta & = & 4 \\ \sqrt{x^{2}+y^{2}}-x & = & 4 \\ \sqrt{x^{2}+y^{2}} & = & x+4 \\ x^{2}+y^{2} & = & x^{2}+8x+16 \\ y^{2} & = & 8x+16 \\ y^{2} & = & 8\left( x+2\right) . \end{eqnarray*} ésta es la ecuación cartesiana de la parábola horizontal con vértice en el punto de coordenadas \(\left( -2,0\right) \) que se muestra en la figura anterior.
2. Encuentra la ecuación polar de la ecuación cartesiana \(y=x+3.\)

   Solución:

   Como \begin{eqnarray*} x & = & r\cos \theta \\ y & = & r\ \text{sen}\ \theta , \end{eqnarray*} al sustituir, obtenemos: \begin{equation*} r\ \text{sen}\ \theta =r\cos \theta +3. \end{equation*}

   De donde, \begin{eqnarray*} r\ \text{sen}\ \theta -r\cos \theta & = & 3 \\ r\left( \text{sen}\ \theta -\cos \theta \right) & = & 3 \\ r & = & \dfrac{3}{ \text{sen}\ \theta -\cos \theta } \end{eqnarray*}