Coordenadas Polares Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Introducción

Comúnmente, localizamos puntos en el plano usando coordenadas rectangulares, también llamadas cartesianas.

Introducimos aquí un tipo distinto de coordenadas, las coordenadas polares, éstas nos darán en algunos casos una descripción algebraica más sencilla de regiones del plano acotadas por curvas planas. Las coordenadas polares son usadas también para evaluar de manera simple algunas integrales dobles.

Denotaremos las coordenadas polares de un punto por \(\left( r,\theta \right) .\) Es nuestra intención asociar a cada punto \(P\) del plano una pareja \( \left( r,\theta \right) \) y viceversa. Ello lo hacemos de la siguiente manera:

Tomamos un punto fijo \(O\) al que llamamos origen o polo y usando éste como punto inicial trazamos un rayo, usualmente de manera horizontal y extendiéndose a la derecha a partir del polo, al que llamaremos eje polar.

(a) Asociación de un punto a una pareja \(\left( r,\theta \right) \)

Para cada pareja \(\left( r,\theta \right) \) de reales consideramos la semirrecta \(\ell _{\theta },\) con origen en \(O\), que resulta al girar el eje polar un ángulo de \(\theta \) radianes, si \(\theta >0,\) el giro es en sentido contrario al movimiento de las manecillas del reloj.

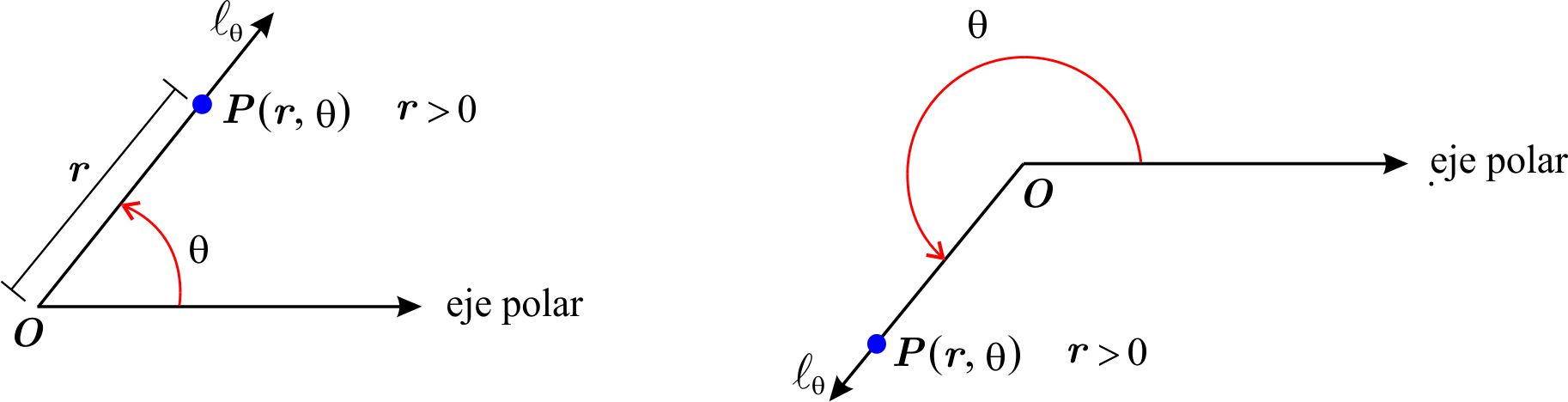
Después completamos \(\ell _{\theta }\) a una recta uniéndole un rayo \( \ell _{\theta }^{\prime }\) y medimos \(r\) unidades a partir del origen, si \(r\) es positivo sobre \(\ell _{\theta }\) y sobre \(\ell _{\theta }^{\prime }\) si \( r \) es negativo; el punto así obtenido, es el asociado a la pareja \( \left( r,\theta \right) \) y lo denotamos por \(P\left( r,\theta \right) \). Decimos que \(P\) tiene coordenadas polares \(\left( r,\theta \right) \) o que \(\left( r,\theta \right) \) son unas coordenadas polares de \(P\)

(b) Asociación de una pareja \(\left( r,\theta \right) \) a un punto

Recíprocamente, a un punto \(P\) del plano, distinto de \(O\), le asociamos la pareja \(\left( r,\theta \right) \) donde \(r\) es la distancia de \( P\) al origen y \(0\leq \theta < 2\pi \) es la medida en radianes del ángulo entre el eje polar y el segmento de recta \(OP.\) De acuerdo con (a), \(\left( r,\theta \right) \) son unas coordenadas polares de \(P\) y son llamadas las coordenadas polares principales de \(P\). Al origen \(O\) se le asocia cualquier pareja de la forma \(\left( 0,\theta \right) ,\) con \(\theta \) arbitrario.

Observaciones:

1. Hay muchos casos en los que no importa si los ángulos se miden en grados o radianes. En otros, por ejemplo para deducir las fórmulas de derivación de las funciones trigonométricas, es necesario usar radianes. En lo que sigue usaremos radianes para medir los ángulos.
2. Una infinidad de parejas \(\left( r,\theta \right) \) tienen asociado el mismo punto en el plano mediante el procedimiento indicado en (a). Esto es evidente puesto que los ángulos \(\theta \) y \(\theta +2n\pi ,\ n\in \mathbb{Z}\) determinan el mismo rayo; es decir, \(\ell _{\theta }=\ell _{\theta +2n\pi }\). Así por ejemplo \(\left( r,\theta +2n\pi \right) ,\) \( \left( r,\theta -2\pi \right) ,\) \(\left( r,\theta \right) \) son coordenadas polares para un mismo punto.
3. La dirección contraria a la dada por el valor \(\theta \) está determinada por \(\theta +\pi \), es decir, \(\ell _{\theta }^{\prime }=\ell _{\theta +\pi }\) y \(\ell _{\theta +\pi }^{\prime }=\ell _{\theta }\). Entonces las parejas \(\left( r,\theta \right) \) y \(\left( -r,\theta +\pi \right) \) son dos coordenadas polares del mismo punto.
4. Sea \(P\) un punto en el plano con coordenadas polares \(\left( r,\theta \right) ,\) entonces cualesquiera otras coordenadas de \(P\) son de la forma \begin{equation*} \left( r,\theta +2n\pi \right) \qquad \text{o}\qquad \left( -r,\theta +\pi +2n\pi \right) =\left( -r,\theta +\left( 2n+1\right) \pi \right) \qquad \text{con }n\in \mathbb{Z}. \end{equation*}

   En efecto, por (2) \(\left( r,\theta \right) \) y \(\left( r,\theta +2n\pi \right) \) son coordenadas polares de \(P\) y por (3), \(\left( r,\theta +2n\pi \right) \) y \(\left( -r,\theta +\pi +2n\pi \right) \) son coordenadas polares del mismo punto, es decir de \(P.\)

5. Como ya vimos, para cualquier punto en el plano, podemos encontrar coordenadas polares \(\left( r,\theta \right) \) de tal manera que \(r>0\) y \( \theta \in \left[ 0,2\pi \right) \) (las coordenadas principales). Sin embargo, también es cierto que todo punto tiene coordenadas polares con \( r>0\) y \(\theta \in \left[ -\pi ,\pi \right) .\) En efecto si \(\left( r,\theta \right) \) son las coordenadas principales de \(P\) y \(\pi \leq \theta < 2\pi ,\) entonces \(P\left( r,\theta -2\pi \right) =P\left( r,\theta \right) \) y \(r>0\) y \(-\pi \leq \theta -2\pi < 0.\)

En general, podemos escoger \(\theta \) en cualquier intervalo de longitud \( 2\pi .\) Como veremos más adelante, dependiendo del problema, elegiremos entre estos intervalos el que resulte más adecuado.

Relación entre los sistemas de coordenadas cartesianas y polares

Con frecuencia es útil usar coordenadas polares y cartesianas en un mismo problema. En ese caso se hace coincidir el origen y el eje \(X\) positivo del sistema de coordenadas rectangulares con el polo y el eje polar, respectivamente.

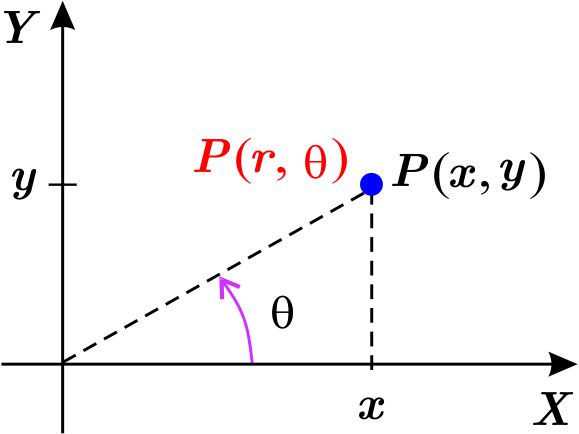
Así, si \(P\) es un punto arbitrario distinto del origen \(O\) y, \(\left(x,y\right) \) y \(\left( r,\theta \right)\) son las coordenadas rectangulares y polares principales de \(P\), deducimos de la figura las siguientes relaciones: \begin{equation*} x^{2}+y^{2}=r^{2},\qquad \text{sen}\ \theta =\dfrac{y}{\sqrt{x^{2}+y^{2}}} ,\qquad \cos \theta =\dfrac{x}{\sqrt{x^{2}+y^{2}}} \end{equation*} De donde, si conocemos las coordenadas polares \(\left( r,\theta \right)\) de un punto, entonces sus coordenadas cartesianas son: \begin{equation*} x=r\cos \theta ,\qquad \qquad \qquad y=r\ \text{sen}\ \theta . \end{equation*} Inversamente, si conocemos as coordenadas cartesianas \(\left(x,y\right)\) del punto, entonces \begin{equation*} r=\sqrt{x^{2}+y^{2}}\qquad \qquad \qquad \tan \theta =\frac{y}{x}\text{ si } x\neq 0 \end{equation*}

Las coordenadas polares principales son \begin{equation*} r=\sqrt{x^{2}+y^{2}} \end{equation*} y \begin{equation} \theta =\left\{ \begin{array}{ll} \arctan \left( \dfrac{y}{x}\right) & \text{si } x>0, y\geq 0 \text{ (o sea,} \left(x,y\right) \text{ en el 1er cuadrante)} \\ \arctan \left( \dfrac{y}{x}\right) +\pi & \text{si } x < 0, y\in \mathbb{R} \ \text{(o sea,} \left( x,y\right) \text{ en el 2o o 3er cuadrantes)} \\ \arctan \left( \dfrac{y}{x}\right) +2\pi & \text{si } x>0, y < 0 \ \text{(o sea,} \left( x,y\right) \text{ en el 4o cuadrante).} \\ 0 & \text{si } x=0 ~ \text{y } y=0 \\ \dfrac{\pi }{2} & \text{si } x=0 ~ \text{y } y > 0 \\ \dfrac{3\pi }{2} & \text{si } x=0 ~ \text{y } y < 0 \end{array} \right. \label{angulo} \tag{1} \end{equation}

donde usamos la función \(\arctan :\mathbb{R\longrightarrow }\left( -\dfrac{\pi }{2},\dfrac{\pi }{2}\right) \). Lo anterior se debe a que \(\arctan \dfrac{y}{x}\in \left[ 0,\dfrac{\pi }{2}\right) \) si \(\dfrac{y}{x}\geq 0\) y \( \arctan \dfrac{y}{x}\in \left( -\dfrac{\pi }{2},0\right) \) si \(\dfrac{y}{x} < 0.\)

Observación Pudiera parecer que las relaciones \begin{equation*} x=r\cos \theta \qquad \qquad \qquad y=r\ \text{sen}\ \theta \end{equation*} sólo se satisfacen si \(\left( r,\theta \right) \) son las coordenadas polares principales del punto de coordenadas cartesianas \(\left( x,y\right) \) , pero esto no es así, sino que son satisfechas por cualesquiera de las coordenadas polares del punto. En efecto, si \(\left( r^{\prime },\theta ^{\prime }\right) \) son unas coordenadas polares de \(P\left( x,y\right) \) y \(\left( r,\theta \right) \) son sus coordenadas polares principales, entonces \(\left( r^{\prime },\theta ^{\prime }\right) =\left( r,\theta +2n\pi \right) \) o bien, \(\left( r^{\prime },\theta ^{\prime }\right) =\left( -r,\theta +\pi +2n\pi \right) \) con \(n\in \mathbb{Z}\). En cada caso tenemos: \begin{eqnarray*} x & = & r\cos \theta =r\cos \left( \theta +2n\pi \right) =r^{\prime }\cos \theta ^{\prime } \\ y & = & r\ \text{sen}\ \theta =r\ \text{sen}\ \left( \theta +2n\pi \right) =r^{\prime }\ \text{sen}\ \theta ^{\prime } \end{eqnarray*} o bien, \begin{eqnarray*} x & = & r\cos \theta =-r\cos \left( \theta +\pi +2n\pi \right) =r^{\prime }\cos \theta ^{\prime } \\ y & = & r\ \text{sen}\ \left( \theta +2n\pi \right) =-r\ \text{sen}\ \left( \theta +\pi +2n\pi \right) =r^{\prime }\ \text{sen}\ \theta ^{\prime }. \end{eqnarray*}

Ejemplos

1. Encuentra las coordenadas polares principales del punto cuyas coordenadas rectangulares son \(\left( -2,2\sqrt{3}\right) .\)

   Solución:

   Puesto que \begin{equation*} x=-2,\qquad \qquad \qquad y=2\sqrt{3}, \end{equation*} utilizando la relación entre las coordenadas polares y cartesianas, tenemos \begin{equation*} r^{2}=x^{2}+y^{2}=4+12=16 \end{equation*} así \begin{equation*} r=4 \end{equation*} y \begin{eqnarray*} \text{sen}\ \theta &=&\dfrac{y}{\sqrt{x^{2}+y^{2}}}=\dfrac{2\sqrt{3}}{4}= \dfrac{\sqrt{3}}{2} \\ \cos \theta &=&\dfrac{x}{\sqrt{x^{2}+y^{2}}}=-\dfrac{2}{4}=-\dfrac{1}{2}, \end{eqnarray*} de donde \begin{equation*} \arctan \left( \dfrac{2\sqrt{3}}{-2}\right) =\arctan \left( -\sqrt{3}\right) =-\dfrac{\pi }{3}. \end{equation*}

   Puesto que \(\left( -2,2\sqrt{3}\right) \) está en el segundo cuadrante hay que sumar \(\pi \) al ángulo arriba obtenido (ver (\ref{angulo})). Por tanto, \(\theta =-\dfrac{\pi }{3}+\pi =\dfrac{2}{3}\pi .\)

2. Encuentra las coordenadas rectangulares del punto con coordenadas polares \(\left( -6,\dfrac{3\pi }{4}\right) .\)

   Solución:

   Tenemos \begin{equation*} r=-6\qquad \qquad \qquad \theta =\dfrac{3\pi }{4} \end{equation*} De acuerdo con la observación sobre la relación entre las coordenadas polares y rectangulares, obtenemos \begin{eqnarray*} x & = & r\cos \theta =-6\cos \dfrac{3\pi }{4}=-6\left( -\dfrac{\sqrt{2}}{2} \right) =3\sqrt{2} \\ y & = & r\ \text{sen}\ \theta =-6\ \text{sen}\dfrac{3\pi }{4}=-6\dfrac{\sqrt{2} }{2}=-3\sqrt{2} \end{eqnarray*} de donde, \(\left( 3\sqrt{2},-3\sqrt{2}\right) \) son la coordenadas rectangulares del punto.

3. Dibuja en el plano cartesiano el punto \(\left( -2,-2\right) \) y el que tiene coordenadas polares \(\left( 2\sqrt{2},\dfrac{5\pi }{4}\right) .\)

   Solución:

   Localizamos primero el punto \(\left( -2,-2\right) .\)

   

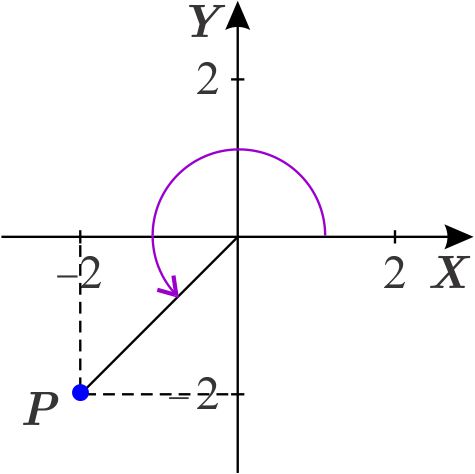
   Encontraremos ahora las coordenadas cartesianas del punto \(\left( 2\sqrt{2}, \dfrac{5\pi }{4}\right) \): \begin{equation*} r=2\sqrt{2} \end{equation*} además \begin{equation*} \cos \dfrac{5\pi }{4}=-\dfrac{\sqrt{2}}{2},\qquad \text{sen}\dfrac{5\pi }{ 4}=-\dfrac{\sqrt{2}}{2} \end{equation*} entonces \begin{equation*} x=2\sqrt{2}\left( -\dfrac{\sqrt{2}}{2}\right) =-2,\qquad y=2\sqrt{2}\left( - \dfrac{\sqrt{2}}{2}\right) =-2 \end{equation*} de donde \begin{equation*} x=-2,\qquad y=-2; \end{equation*} es decir, se trata del mismo punto. Entonces las coordenadas polares del punto \(\left( -2,-2\right) \) son \(\left( 2\sqrt{2},\dfrac{5\pi }{4}\right) \).

Ejercicios

1. \(\left( 1,\dfrac{\pi }{2}\right) .\)

2. \(\left( 4,\dfrac{\pi }{4}\right) .\)

3. \(\left( 2,\dfrac{\pi }{3}\right) .\)

4. \(\left( 2,\dfrac{\pi }{6}\right) .\)

5. \(\left( 1,0\right) .\)

6. \(\left( -5,\pi \right) .\)

7. \(\left( -1,-\dfrac{3\pi }{4}\right) .\)

8. \(\left( \dfrac{1}{2},\dfrac{2\pi }{3}\right) .\)

9. \(\left( -\dfrac{5}{4},\dfrac{5\pi }{6}\right) .\)

10. \(\left( 2,\dfrac{3\pi }{2}\right) .\)

11. \(\left( 3,\dfrac{5\pi }{4}\right) .\)

    Hallar las coordenadas cartesianas de los siguientes puntos dados en coordenadas polares y ubicarlos en el plano.

12. \(\left( -1,\dfrac{-4\pi }{3}\right) .\)

13. \(\left( 2,\dfrac{7\pi }{6}\right) .\)

14. \(\left( 0,\dfrac{9\pi }{4}\right) .\)

15. \(\left( \sqrt{2},\dfrac{7\pi }{4}\right) .\)

16. \(\left( 3,-\dfrac{\pi }{3}\right) .\)

17. \(\left( \dfrac{2}{3},-\pi \right) .\)

18. \(\left( 3,2\pi \right) .\)

19. \(\left( -\sqrt{2},\dfrac{5\pi }{3}\right) .\)

20. \(\left( -4,\dfrac{-11\pi }{6}\right) .\)

21. \(\left( 4,\dfrac{9\pi }{4}\right) .\)

    Dar las coordenadas polares de los puntos con las siguientes coordenadas cartesianas

22. \(\left( -2\sqrt{3},2\right) .\)

23. \(\left( 3,3\sqrt{3}\right) .\)

24. \(\left( \dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}}\right) .\)

25. \(\left( 1,0\right) .\)

26. \(\left( \pi ,\pi \right) .\)

27. \(\left( \sqrt{3},-1\right) .\)

28. \(\left( 0,3\right) .\)

29. \(\left( \sqrt{18},\sqrt{6}\right) .\)

30. \(\left( -\dfrac{3}{4},-\dfrac{3}{4}\right) .\)

31. \(\left( \sqrt{5},\sqrt{15}\right) .\)

32. \(\left( 0,-5\right) .\)

33. ¿Dónde están en el plano \(XY\) los puntos con coordenadas polares de la forma \(\left( r,0\right) \) con \(r>0\)?

34. Demuestra que la distancia entre dos puntos \(P_{1}\left( r_{1},\theta _{1}\right) \) y \(P_{2}\left( r_{2},\theta _{2}\right) \) dados en coordenadas polares es \(\sqrt{r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\cos \left( \theta _{1}-\theta _{2}\right) }.\)

35. Hallar la distancia entre los puntos cuyas coordenadas polares son:
    1. \(\left( 3,\dfrac{5\pi }{6}\right) \) y \(\left( 1,\dfrac{2\pi }{3} \right) .\)

    2. \(\left( 2,\dfrac{\pi }{2}\right) \) y \(\left( 1,-\dfrac{11\pi }{6} \right) .\)

    3. \(\left( 2,\dfrac{7\pi }{4}\right) \) y \(\left( 3,\dfrac{3\pi }{4} \right) .\)

    4. \(\left( 1,\dfrac{9\pi }{4}\right) \) y \(\left( 1,-\dfrac{11\pi }{4} \right) .\)

36. Dibujar las regiones dadas por las siguientes desigualdades.
    1. \(0\leq \theta \leq \dfrac{\pi }{4},\qquad 1\leq r\leq 3.\)

    2. \(\theta =\dfrac{\pi }{6},\qquad r\geq 0.\)

    3. \(\dfrac{3\pi }{4}\leq \theta \leq \dfrac{5\pi }{4},\qquad 2\leq r\leq 5.\)

    4. \(\dfrac{\pi }{6}\leq \theta \leq \dfrac{\pi }{3}.\)

    5. \(\theta =\dfrac{2\pi }{3},\qquad -2\leq r\leq 4.\)

    6. \(\theta =\dfrac{5\pi }{4},\qquad -3\leq r\leq 1.\)

    7. \(\sqrt{2}\leq r\leq 2.\)

    8. \(0\leq \theta \leq \dfrac{\pi }{8},\qquad r>0.\)