 |
Coordenadas Polares
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos
Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)
\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM
|  |
|
Concoides de Nicomedes
Nos referimos ahora a una familia de curvas llamadas concoides de Nicómedes,
las cuales tienen por ecuación polar:
\begin{equation*}
r=a+b\sec \theta ,\qquad a,b\in \mathbb{R}.
\end{equation*}
Claramente éstas son simétricas con respecto al eje \(X.\)
El nombre de estas curvas se debe a que se asemejan a una concha.
Ahora analizamos el caso en que \(a,b>0.\)
Dibujemos en el plano cartesiano \(\Theta R\) la gráfica de \(r=b\sec
\theta \), en el intervalo \(\left[ 0,2\pi \right] \):
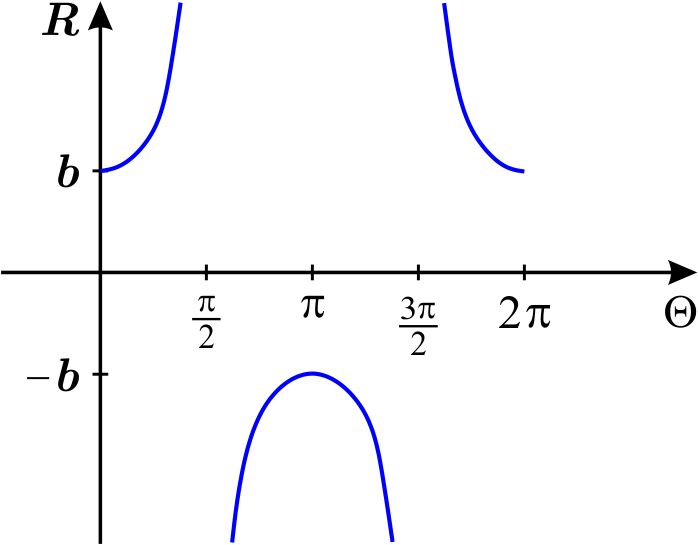
Así, la gráfica cartesiana de \(r=a+b\sec \theta \) es:
- Si \(a=b\)

- Si \(a>b\)

- Si \(a < b\)

Como en los ejemplos anteriores, sustituyendo \(r=a+b\sec \theta \) en la
coordenada cartesiana \(y=r\ \text{sen}\ \theta \) de un punto de la concoide
tenemos:
\begin{eqnarray*}
y &=&\left( a+b\sec \theta \right) \ \text{sen}\ \theta \\
&=&a\ \text{sen}\ \theta +b\tan \theta
\end{eqnarray*}
Analizaremos el comportamiento de \(y\) cuando \(\theta \) se aproxima a \(\dfrac{
\pi }{2}\) y \(\dfrac{3\pi }{2}\) por la derecha y por la izquierda
\begin{eqnarray*}
\lim\limits_{\theta \rightarrow \frac{\pi }{2}^{-}}\left( a\ \text{sen}\
\theta +b\tan \theta \right) & = & +\infty =\lim\limits_{\theta \rightarrow
\frac{3\pi }{2}^{+}}\left( a\ \text{sen}\ \theta +b\tan \theta \right) \\
\lim\limits_{\theta \rightarrow \frac{\pi }{2}^{+}}\left( a\ \text{sen}\
\theta +b\tan \theta \right) & = & -\infty =\lim\limits_{\theta \rightarrow
\frac{3\pi }{2}^{-}}\left( a\ \text{sen}\ \theta +b\tan \theta \right)
\end{eqnarray*}
Ahora analizaremos el comportamiento de la coordenada cartesiana \(x=r\cos
\theta \) de un punto de la concoide cuando \(\theta \) se aproxima a \(\dfrac{
\pi }{2}\) y \(\dfrac{3\pi }{2}.\)
\begin{eqnarray*}
x & = & r\cos \theta \\
& = & \left( a+b\sec \theta \right) \cos \theta \\
& = & a\cos \theta +b
\end{eqnarray*}
y
\begin{equation*}
\lim\limits_{\theta \rightarrow \frac{\pi }{2}}\left( a\cos \theta +b\right)
=b=\lim\limits_{\theta \rightarrow \frac{3\pi }{2}}\left( a\cos \theta
+b\right)
\end{equation*}
La gráfica polar de la concoide \(r=a+b\sec \theta \) es:
- Si \(a=b\):

- Si \(a>b\):
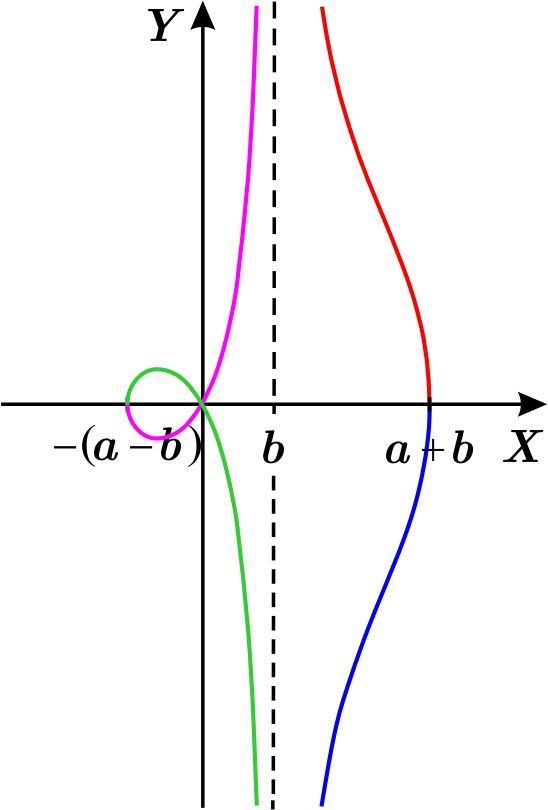
- Si \(a < b\):
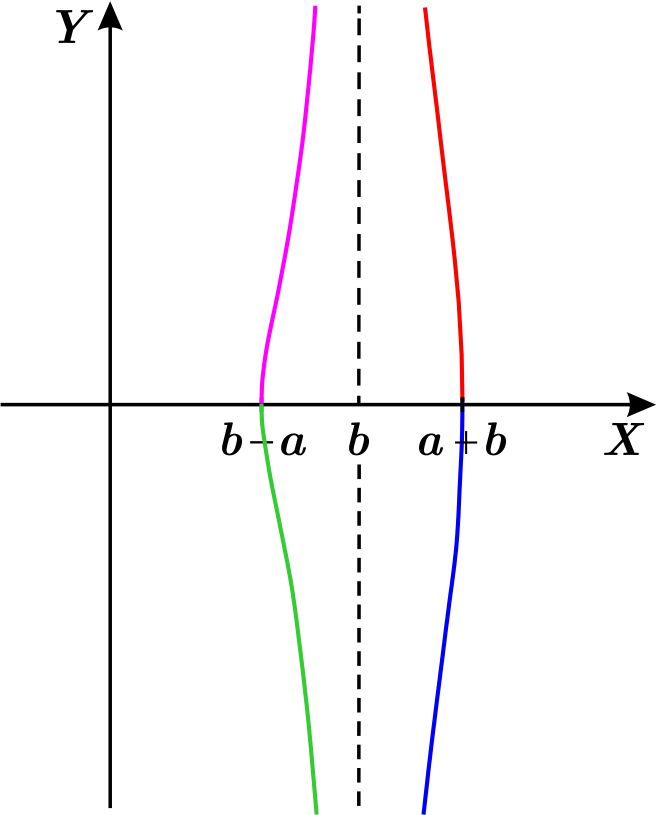
Ejercicios
Dibuja las gráficas de las siguientes ecuaciones.
- \(r=3+2\sec \theta .\)
- \(r=1+\sec \theta .\)
- \(r=1+4\sec \theta .\)
- \(r=1-3\sec \theta .\)
- \(r=5-2\sec \theta .\)
- \(r=6-6\sec \theta .\)
Universidad Nacional Autónoma de México










