Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 4

Solución::

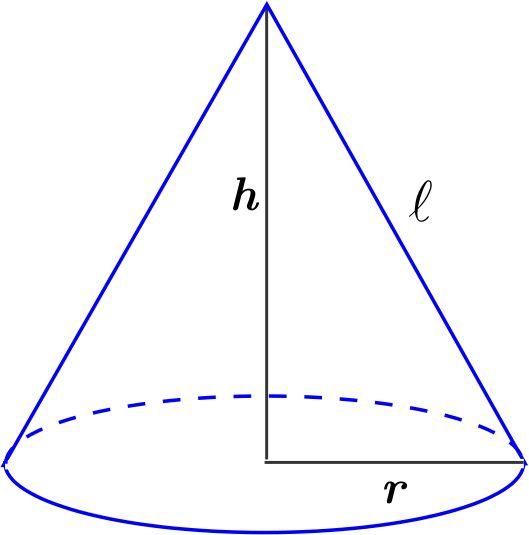
La generatriz \(\ell \) se calcula, por el Teorema de Pitágoras como \begin{equation*} \ell =\sqrt{h^{2}+r^{2}}. \end{equation*} La cantidad de material es el área del sector \(x\) de un círculo \(c\) de radio \(\ell \) y cuyo arco es \(2\pi r.\)

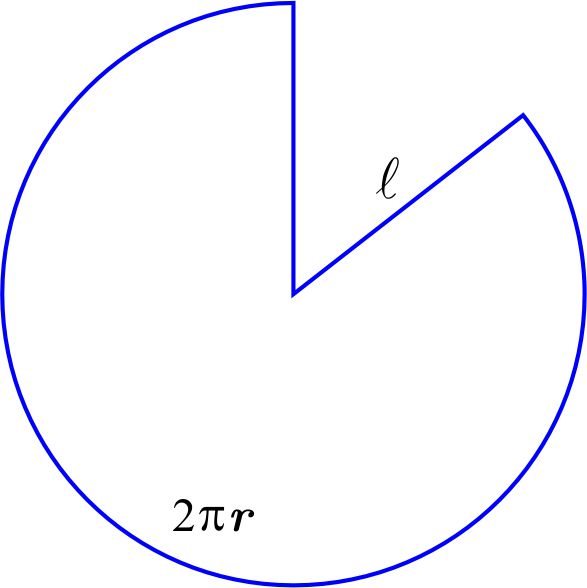
El área del círculo \(c\) es: \(\pi \ell ^{2}.\)

Llamamos \(x\) al área del sector. Las áreas del círculo y el sector son proporcionales, \begin{equation*} \dfrac{\pi \ell ^{2}}{2\pi \ell }=\dfrac{x}{2\pi r}, \end{equation*} de donde el área del sector \(x\) es \begin{equation*} x=\dfrac{\pi \ell ^{2}\left( 2\pi r\right) }{2\pi \ell }=\pi r\ell =\pi r \sqrt{h^{2}+r^{2}}. \end{equation*} El volumen del cono es \begin{equation*} 64=\dfrac{1}{3}\pi r^{2}h. \end{equation*} Definimos \begin{equation*} f\left( r,h\right) =\pi r\sqrt{h^{2}+r^{2}}. \end{equation*} Debemos encontrar los valores de \(r\) y \(h\) para los cuales la función \(f\) sujeta a la restricción \begin{equation*} 64=\dfrac{1}{3}\pi r^{2}h, \end{equation*} tiene un valor mínimo.

Al definir \begin{equation*} g\left( r,h\right) =\dfrac{1}{3}\pi r^{2}h-64, \end{equation*} la restricción se escribe como \begin{equation*} g\left( r,h\right) =0. \end{equation*} Calculamos los gradientes de \(f\) y \(g\): \begin{eqnarray*} \nabla f\left( r,h\right) & = & \left( \dfrac{\partial f}{\partial r},\dfrac{ \partial f}{\partial h}\right) \\ & = & \left( \dfrac{2\pi r^{2}+\pi h^{2}}{\sqrt{h^{2}+r^{2}}},\dfrac{\pi rh}{ \sqrt{h^{2}+r^{2}}}\right) \end{eqnarray*} y \begin{equation*} \nabla g\left( r,h\right) =\left( \dfrac{\partial g}{\partial r},\dfrac{ \partial g}{\partial h}\right) =\left( \dfrac{2}{3}\pi rh,\dfrac{1}{3}\pi r^{2}\right) . \end{equation*} De acuerdo con el método de Lagrange, debemos resolver el sistema \begin{eqnarray*} \nabla f\left( r,h\right) & = & \lambda \nabla g\left( r,h\right) \\ \dfrac{1}{3}\pi r^{2}h & = & 64 \end{eqnarray*} para encontrar los candidatos donde pueden alcanzarse valores extremos.

Tenemos \begin{eqnarray*} \dfrac{2\pi r^{2}+\pi h^{2}}{\sqrt{h^{2}+r^{2}}} & = & \dfrac{2}{3}\lambda \pi rh \\ \dfrac{\pi rh}{\sqrt{h^{2}+r^{2}}} & = & \dfrac{1}{3}\lambda \pi r^{2} \\ \dfrac{1}{3}\pi r^{2}h & = & 64. \end{eqnarray*} Simplificando obtenemos \begin{eqnarray} \dfrac{2r^{2}+h^{2}}{\sqrt{h^{2}+r^{2}}} & = & \dfrac{2}{3}\lambda rh \label{5} \tag{1} \\ \dfrac{h}{\sqrt{h^{2}+r^{2}}} & = & \dfrac{1}{3}\lambda r \notag \\ \dfrac{1}{3}\pi r^{2}h & = & 64. \notag \end{eqnarray} Sabemos que \(r\neq 0,\) \(h\neq 0\) y también \(\lambda \neq 0\), ya que en caso contrario la segunda ecuación no se cumpliría. Despejando \( \sqrt{h^{2}+r^{2}}\) de las dos ecuaciones del sistema anterior, tenemos \begin{eqnarray*} \sqrt{h^{2}+r^{2}} & = & \dfrac{2r^{2}+h^{2}}{\dfrac{2}{3}\lambda rh} \\ \sqrt{h^{2}+r^{2}} & = & \dfrac{h}{\dfrac{1}{3}\lambda r}, \end{eqnarray*} de donde, \begin{eqnarray*} \dfrac{1}{3}\lambda r\left( 2r^{2}+h^{2}\right) & = & \dfrac{2}{3}\lambda rh^{2} \\ r^{2} & = & \dfrac{h^{2}}{2}. \end{eqnarray*} Sustituyendo el valor de \(r^{2}\) en la tercera ecuación de (\ref{5}), obtenemos: \begin{eqnarray*} \dfrac{1}{3}\pi r^{2}h & = & 64 \\ \dfrac{1}{3}\pi \dfrac{h^{2}}{2}h & = & 64 \\ h & = & 4\sqrt[3]{\dfrac{6}{\pi }} \end{eqnarray*} como \(r^{2}=\dfrac{h^{2}}{2},\) entonces \begin{eqnarray*} r^{2} & = & \dfrac{1}{2}\left( 4\sqrt[3]{\dfrac{6}{\pi }}\right) ^{2} \\ r & = & \sqrt{8}\sqrt[3]{\dfrac{6}{\pi }}. \end{eqnarray*} Ahora sustituimos \(r^{2}=\dfrac{h^{2}}{2}\) en la primera ecuación de ( \ref{5}): \begin{eqnarray*} \dfrac{2r^{2}+h^{2}}{\sqrt{h^{2}+r^{2}}} & = & \lambda \dfrac{2}{3}rh \\ \dfrac{2\left( \dfrac{h^{2}}{2}\right) +h^{2}}{\sqrt{h^{2}+\dfrac{h^{2}}{2}}} & = & \lambda \dfrac{2}{3}\left( \dfrac{h}{\sqrt{2}}\right) h \\ \dfrac{6}{\sqrt{3}h} & = & \lambda . \end{eqnarray*} Sustituyendo el valor \(h=4\sqrt[3]{\dfrac{6}{\pi }}\) obtenido antes, tenemos: \begin{equation*} \lambda =\dfrac{6}{\sqrt{3}\left( 4\sqrt[3]{\dfrac{6}{\pi }}\right) }=\dfrac{ \sqrt{3}}{2}\sqrt[3]{\dfrac{\pi }{6}}. \end{equation*} Así \begin{equation*} r=\sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}} \quad \quad h=4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}} \quad \quad \text{y} \quad \quad \lambda =\dfrac{\sqrt{3}}{2}\left( \dfrac{\pi }{6}\right) ^{\frac{1}{3}}. \end{equation*} Usaremos el criterio del determinante hessiano límitado para saber si en el punto encontrado \(\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{ 1}{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) \) la función \(f\) tiene un máximo o mínimo sujeto a la restricción \(\dfrac{1}{ 3}\pi r^{2}h=64.\)

Definimos la función auxiliar \begin{eqnarray*} p\left( r,h\right) & = & f\left( r,h\right) -\lambda g\left( r,h\right) \\ & = & \pi r\sqrt{h^{2}+r^{2}}-\lambda \left( \dfrac{1}{3}\pi r^{2}h-64\right) . \end{eqnarray*} Calculamos las derivadas de \(p\) de orden \(1\). \begin{eqnarray*} \dfrac{\partial p }{\partial r}\left( r,h\right) & = & \dfrac{2\pi r^{2}+\pi h^{2}}{\sqrt{h^{2}+r^{2}}}-\lambda \left( \dfrac{2}{3}\pi rh\right) \\ \dfrac{\partial p }{\partial h}\left( r,h\right) & = & \dfrac{\pi rh}{\sqrt{ h^{2}+r^{2}}}-\lambda \left( \dfrac{1}{3}\pi r^{2}\right) . \end{eqnarray*} Las derivadas parciales de \(p\) de orden \(2\) son: \begin{eqnarray*} \dfrac{\partial ^{2}p }{\partial r^{2}}\left( r,h\right) & = & \dfrac{\sqrt{ h^{2}+r^{2}}\left( 4\pi r\right) -\left( 2\pi r^{2}+\pi h^{2}\right) \dfrac{r }{\sqrt{h^{2}+r^{2}}}}{h^{2}+r^{2}}-\dfrac{2}{3}\lambda \pi h \\ & = & \dfrac{3\pi h^{2}r+2\pi r^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}- \dfrac{2}{3}\lambda \pi h, \\ & & \\ \dfrac{\partial ^{2}p }{\partial h^{2}}\left( r,h\right) & = & \dfrac{\sqrt{ h^{2}+r^{2}}\left( \pi r\right) -\pi rh\dfrac{h}{\sqrt{h^{2}+r^{2}}}}{ h^{2}+r^{2}} \\ & = & \dfrac{\pi r^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}} \end{eqnarray*} y \begin{eqnarray*} \dfrac{\partial ^{2}p }{\partial r\partial h}\left( r,h\right) & = & \dfrac{ \sqrt{h^{2}+r^{2}}\left( \pi h\right) -\pi rh\dfrac{r}{\sqrt{h^{2}+r^{2}}}}{ h^{2}+r^{2}}-\dfrac{2}{3}\lambda \pi r \\ & = & \dfrac{\pi h^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}-\dfrac{2}{3} \lambda \pi r \\ & & \\ \dfrac{\partial ^{2}p }{\partial h\partial r}\left( r,h\right) & = & \dfrac{ \sqrt{h^{2}+r^{2}}\left( 2\pi h\right) -\left( 2\pi r^{2}+\pi h^{2}\right) \dfrac{h}{\sqrt{h^{2}+r^{2}}}}{h^{2}+r^{2}}-\dfrac{2}{3}\lambda \pi r \\ & = & \dfrac{\pi h^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}-\dfrac{2}{3} \lambda \pi r. \end{eqnarray*} Evaluamos las derivadas de segundo orden de \(p\) en los valores \begin{equation*} r=\sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}} \quad \quad h=4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}} \quad \quad \text{y} \quad \quad \lambda =\dfrac{\sqrt{3}}{2}\left( \dfrac{\pi }{6}\right) ^{\frac{1}{3}}, \end{equation*} para lo cual calculamos primero \begin{eqnarray*} \left( h^{2}+r^{2}\right) ^{\frac{3}{2}} & = & \left( \left( 4\left( \dfrac{6}{ \pi }\right) ^{\frac{1}{3}}\right) ^{2}+\left( \sqrt{8}\left( \dfrac{6}{\pi } \right) ^{\frac{1}{3}}\right) ^{2}\right) ^{\frac{3}{2}} \\ & = & 24^{\frac{3}{2}}\left( \dfrac{6}{\pi }\right) . \end{eqnarray*} Ahora evaluamos \begin{eqnarray*} \dfrac{\partial p^{2} }{\partial r^{2}}\left( r,h\right) & = & \dfrac{3\pi h^{2}r+2\pi r^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}-\dfrac{2}{3} \lambda \pi h \\ & = & \dfrac{\pi r\left( 3h^{2}+2r^{2}\right) }{\left( h^{2}+r^{2}\right) ^{ \frac{3}{2}}}-\dfrac{2}{3}\lambda \pi h. \end{eqnarray*} El primer sumando es \begin{equation*} \dfrac{\pi \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\left( 3\left( 16\left( \dfrac{6}{\pi }\right) ^{\frac{2}{3}}\right) +2\left( 8\left( \dfrac{6}{\pi }\right) ^{\frac{2}{3}}\right) \right) }{24^{\frac{3}{2 }}\left( \dfrac{6}{\pi }\right) }=\dfrac{8}{9}\sqrt{3}\pi \end{equation*} el segundo \begin{eqnarray*} -\dfrac{2}{3}\lambda \pi h & = & -\dfrac{2}{3}\pi \dfrac{\sqrt{3}}{2}\left( \dfrac{\pi }{6}\right) ^{\frac{1}{3}}4\left( \dfrac{6}{\pi }\right) ^{\frac{1 }{3}} \\ & = & -\dfrac{4\sqrt{3}}{3}\pi . \end{eqnarray*} De donde, \begin{equation*} \dfrac{\partial ^{2}p }{\partial r^{2}}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{ 3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right)= \dfrac{8\sqrt{3}}{9}\pi -\dfrac{4\sqrt{3}}{3}\pi =-\dfrac{4}{9}\sqrt{3}\pi . \end{equation*} En tanto que para \(\dfrac{\partial ^{2}p }{\partial h^{2}}\left( r,h\right)= \dfrac{\pi r^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}\) se tiene \begin{eqnarray*} \dfrac{\partial ^{2}p }{\partial h^{2}}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{ 3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) & = & \dfrac{\pi \left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3} }\right) ^{3}}{24^{\frac{3}{2}}\left( \dfrac{6}{\pi }\right) }\text{ } \\ & = & \dfrac{\pi }{3\sqrt{3}} \end{eqnarray*} y para la derivada mixta \(\dfrac{\partial ^{2}p }{\partial r\partial h}\left( r,h\right)=\dfrac{\pi h^{3}}{\left( h^{2}+r^{2}\right) ^{\frac{3}{2}}}- \dfrac{2}{3}\lambda \pi r \) \begin{eqnarray*} \dfrac{\partial ^{2}p }{\partial r\partial h} \left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{ 3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) & = & \dfrac{\pi \left( 4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3 }}\right) ^{3}}{24^{\frac{3}{2}}\left( \dfrac{6}{\pi }\right) }-\dfrac{2}{3} \pi \dfrac{\sqrt{3}}{2}\left( \dfrac{\pi }{6}\right) ^{\frac{1}{3}}\sqrt{8} \left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}} \\ & = & -\dfrac{4}{9}\sqrt{6}\pi . \end{eqnarray*} Evaluamos las derivadas parciales de \(g\): \begin{eqnarray*} \dfrac{\partial g}{\partial r} \left( r,h\right) &=&\dfrac{2}{3}\pi rh \\ \dfrac{\partial g}{\partial r}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{ \frac{1}{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) & = & \dfrac{2 }{3}\pi \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}4\left( \dfrac{6 }{\pi }\right) ^{\frac{1}{3}} \\ & = & \dfrac{8\sqrt{8}}{3}\pi \left( \dfrac{6}{\pi }\right) ^{\frac{2}{3}} \end{eqnarray*} y \begin{eqnarray*} \dfrac{\partial g}{\partial h}\left( r,h\right) & = &\dfrac{1}{3}\pi r^{2}\\ \dfrac{\partial g}{\partial h}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{ \frac{1}{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) & = & \dfrac{1 }{3}\pi \left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) ^{2} \\ & = & \dfrac{8}{3}\pi \left( \dfrac{6}{\pi }\right) ^{\frac{2}{3}}. \end{eqnarray*} El hessiano limitado es \begin{eqnarray*} \left\vert \overline{H}\left( r,h\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & \dfrac{\partial g}{\partial r}\left( r,h\right) & \dfrac{\partial g}{ \partial h}\left( r,h\right) \\ & & \\ \dfrac{\partial g}{\partial r}\left( r,h\right) & \dfrac{\partial ^{2}p}{ \partial r^{2}}\left( r,h\right) & \dfrac{\partial ^{2}p}{\partial h\partial r}\left( r,h\right) \\ & & \\ \dfrac{\partial g}{\partial h}\left( r,h\right) & \dfrac{\partial ^{2}p}{ \partial r\partial h}\left( r,h\right) & \dfrac{\partial ^{2}p}{\partial h^{2}}\left( r,h\right) \end{array} \right\vert \\ \end{eqnarray*} Lo evaluamos en \(\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1 }{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right)\): \begin{eqnarray*} \left\vert \overline{H}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1 }{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & \dfrac{8}{3}\sqrt{8}\pi \left( \dfrac{6}{\pi }\right) ^{2/3} & \dfrac{8}{ 3}\pi \left( \dfrac{6}{\pi }\right) ^{2/3} \\ & & \\ \dfrac{8}{3}\sqrt{8}\pi \left( \dfrac{6}{\pi }\right) ^{2/3} & -\dfrac{4}{9} \sqrt{3}\pi & -\dfrac{4}{9}\sqrt{6}\pi \\ & & \\ \dfrac{8}{3}\pi \left( \dfrac{6}{\pi }\right) ^{2/3} & -\dfrac{4}{9}\sqrt{6} \pi & \dfrac{\pi }{3\sqrt{3}} \end{array} \right\vert \end{eqnarray*} de donde, calculando el determinante se tiene: \begin{equation*} \left\vert \overline{H}\left( \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1 }{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) \right\vert =- \dfrac{64}{9}\pi ^{3}\left( \dfrac{6}{\pi }\right) ^{4/3}\left( 4\sqrt{3} \right) \end{equation*} Como \(\left\vert \overline{H}\left( \sqrt{8}\left( \dfrac{6}{\pi } \right) ^{\frac{1}{3}},4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\right) \right\vert < 0\), entonces, por el inciso 2 del Teorema 1, el valor mínimo se alcanza para \(r=\sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}\) y \( h=4\left( \dfrac{6}{\pi }\right) ^{\frac{1}{3}}.\)

Así, el área del sector es \begin{equation*} x=\pi r\sqrt{h^{2}+r^{2}}=\pi \sqrt{8}\left( \dfrac{6}{\pi }\right) ^{\frac{1 }{3}}24^{\frac{3}{2}}\left( \dfrac{6}{\pi }\right) =192\pi \left( \dfrac{6}{ \pi }\right) ^{\frac{2}{3}}. \end{equation*} Por tanto, el cono circular recto de volumen \(V\) para el que se usa la menor cantidad de material, tiene altura \(h=4\left( \dfrac{6}{\pi }\right) ^{ \frac{1}{3}}\) y radio de la base \(r=\sqrt{8}\left( \dfrac{6}{\pi }\right) ^{ \frac{1}{3}}\).