Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 2

Solución:

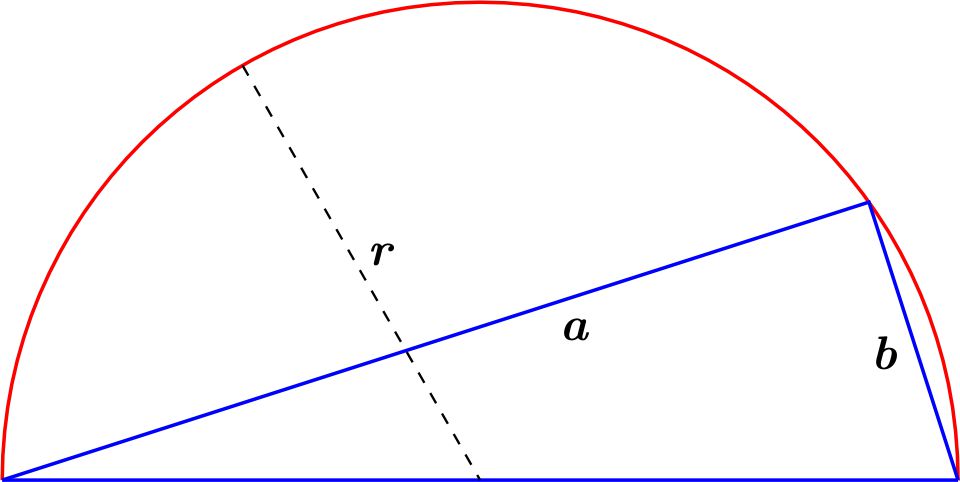
Puesto que el triángulo está inscrito y uno de sus lados es un diámetro del círculo, el triángulo es rectángulo, cuya hipotenusa es un diámetro. Por el Teorema de Pitágoras se tiene que: \begin{equation*} a^{2}+b^{2}=4r^{2}. \end{equation*} Así, el área \(A\) del triángulo es \begin{equation*} A=\dfrac{1}{2}ab. \end{equation*} Definiendo \begin{equation*} f\left( a,b\right) =\dfrac{1}{2}ab, \end{equation*} debemos encontrar los valores de \(a\) y \(b\) para los cuales la función \(f\) sujeta a la restricción \begin{equation*} a^{2}+b^{2}=4r^{2}, \end{equation*} tiene un máximo.

De donde, al definir \begin{equation*} g\left( a,b\right) =a^{2}+b^{2}-4r^{2}, \end{equation*} la restricción se escribe como \begin{equation*} g\left( a,b\right) =0. \end{equation*} Calculamos los gradientes de \(f\) y \(g\): \begin{eqnarray*} \nabla f\left( a,b\right) & = & \left( \dfrac{\partial f}{\partial a},\dfrac{ \partial f}{\partial b}\right) =\left( \dfrac{1}{2}b,\dfrac{1}{2}a\right) \\ \nabla g\left( a,b\right) & = & \left( \dfrac{\partial g}{\partial a},\dfrac{ \partial g}{\partial b}\right) =\left( 2a,2b\right) . \end{eqnarray*} Consideramos el sistema \begin{eqnarray*} \nabla f\left( a,b\right) & = & \lambda \nabla g\left( a,b\right) \\ a^{2}+b^{2} & = & 4r^{2}, \end{eqnarray*} de donde \begin{eqnarray} \dfrac{1}{2}b & = & 2\lambda a \label{2} \tag{1}\\ \dfrac{1}{2}a & = & 2\lambda b \notag \\ a^{2}+b^{2} & = & 4r^{2}. \notag \end{eqnarray} De la primera ecuación de (\ref{2}) tenemos \begin{eqnarray*} b & = & 4\lambda a \\ b^{2} & = & 16\lambda ^{2}a^{2} \end{eqnarray*} y de la segunda \begin{eqnarray*} a & = & 4\lambda b \\ a^{2} & = & 16\lambda ^{2}b^{2}, \end{eqnarray*} por lo que \begin{eqnarray*} a^{2}+b^{2} & = & 16\lambda ^{2}b^{2}+16\lambda ^{2}a^{2} \\ & = & 16\lambda ^{2}\left( a^{2}+b^{2}\right) , \end{eqnarray*} como \(a^{2}+b^{2}\neq 0,\) simplificando tenemos \begin{eqnarray*} 1 & = & 16\lambda ^{2} \\ \dfrac{1}{16} & = & \lambda ^{2}, \end{eqnarray*} de donde \begin{equation*} \lambda =\pm \dfrac{1}{4}. \end{equation*} De las dos primeras ecuaciones de (\ref{2}), puesto que \(a\) y \(b\) son positivos, tenemos que \(\lambda >0,\) por tanto, \(\lambda =\dfrac{1}{4}.\)

Multiplicando la primera ecuación de (\ref{2}) por \(a\) y la segunda por \( b\): \begin{eqnarray*} \dfrac{1}{2}ab & = & 2\lambda a^{2} \\ \dfrac{1}{2}ab & = & 2\lambda b^{2}, \end{eqnarray*} igualando las dos ecuaciones anteriores, tenemos \begin{eqnarray*} 2\lambda a^{2} & = & 2\lambda b^{2} \\ a^{2} & = & b^{2} \\ \left\vert a\right\vert & = & \left\vert b\right\vert \\ a & = & b, \end{eqnarray*} ya que ambos son positivos, con lo cual, de la tercera ecuación de (\ref{2}): \begin{eqnarray*} 2a^{2} & = & 4r^{2} \\ a^{2} & = & 2r^{2} \\ a & = & \sqrt{2}r. \end{eqnarray*} Así, los valores obtenidos son \begin{equation*} a=\sqrt{2}r, \qquad b=\sqrt{2}r, \qquad \lambda =\dfrac{1}{4}. \end{equation*} Consideramos la función \begin{eqnarray*} h\left( a,b\right) & = & f\left( a,b\right) -\lambda g\left( a,b\right) \\ & = & \dfrac{1}{2}ab-\dfrac{1}{4}\left( a^{2}+b^{2}-4r^{2}\right) . \end{eqnarray*} Calculamos las derivadas de \(h\) hasta de orden \(2\): \begin{equation*} \dfrac{\partial h }{\partial a}\left( a,b\right)=\dfrac{1}{2}b-\dfrac{1}{2} a, \qquad \qquad \dfrac{\partial h }{\partial b}\left( a,b\right)=\dfrac{1}{2} a-\dfrac{1}{2}b \end{equation*} y \begin{eqnarray*} \dfrac{\partial ^{2}h }{\partial a^{2}} \left( a,b\right)& = & -\dfrac{1}{2} \\ \dfrac{\partial ^{2}h }{\partial b^{2}}\left( a,b\right) & = & -\dfrac{1}{2} \\ \dfrac{\partial ^{2}h }{\partial a\partial b}\left( a,b\right) & = & \dfrac{1}{2 }=\dfrac{\partial ^{2}h }{\partial b\partial a}\left( a,b\right). \end{eqnarray*} Por otra parte, como \begin{equation*} \nabla g\left( a,b\right) =\left( \dfrac{\partial g}{\partial a},\dfrac{ \partial g}{\partial b}\right) =\left( 2a,2b\right) , \end{equation*} el determinante hessiano limitado es: \begin{eqnarray*} \left\vert \overline{H}\left( a,b\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & \dfrac{\partial g}{\partial a}\left( a,b\right) & \dfrac{\partial g}{ \partial s}\left( a,b\right) \\ & & \\ \dfrac{\partial g}{\partial a}\left( a,b\right) & \dfrac{\partial ^{2}h}{ \partial a^{2}}\left( a,b\right) & \dfrac{\partial ^{2}h}{\partial s\partial a}\left( a,b\right) \\ & & \\ \dfrac{\partial g}{\partial s}\left( a,b\right) & \dfrac{\partial ^{2}h}{ \partial a\partial s}\left( a,b\right) & \dfrac{\partial ^{2}h}{\partial s^{2}}\left( a,b\right) \end{array} \right\vert =\left\vert \begin{array}{ccc} 0 & 2a & 2b \\ & & \\ 2a & -\dfrac{1}{2} & \dfrac{1}{2} \\ & & \\ 2b & \dfrac{1}{2} & -\dfrac{1}{2} \end{array} \right\vert \\ && \\ & = & 2a^{2}+4ab+2b^{2}>0,\text{ ya que tanto }a\text{ como }b \text{ son positivos.} \end{eqnarray*} Así, por el inciso 1 del Teorema 1, \(\left( \sqrt{2}r,\sqrt{2}r\right) \) es un punto máximo relativo de \(f\) bajo la restricción \(g\left( a,b\right) =a^{2}+b^{2}-4r^{2}=0\).

Por tanto, el triángulo de mayor área que se puede inscribir en el semicírculo de radio \(r,\) de tal manera que uno de sus lados sea un diámetro del círculo, es el triángulo rectángulo isosceles cuyos catetos miden \(\sqrt{2}r,\) su área es \begin{equation*} A=\dfrac{1}{2}\left( \sqrt{2}r\right) ^{2}=r^{2}. \end{equation*} Dato curioso. Observa que hemos probado que: \(\pi \) es la razón del área de un círculo al área del triángulo de mayor área que se puede inscribir en el semicírculo correspondiente, de tal manera que uno de sus lados sea un diámetro del círculo.