
Máximos y Mínimos de Funciones de Varias Variables
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

 |
Máximos y Mínimos de Funciones de Varias VariablesAngel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) |  |
Solución:
Ésta es la gráfica de la función \(y^{2}=8x\).
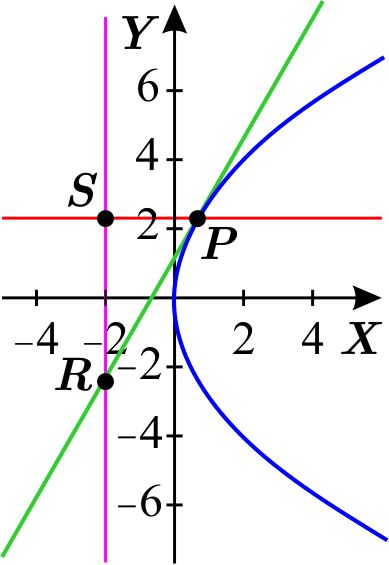
Como la parábola tiene ecuación \(y^{2}=4px,\) entonces \(p>0\). Corresponde a una parábola horizontal con vértice en el origen que abre hacia la derecha. La directriz tiene ecuación \(x=-p.\)
Para determinar el triángulo, consideramos la ecuación de la recta tangente a la parábola en el punto \(P\left( x_{1},y_{1}\right) \) \begin{eqnarray*} y-y_{1} & = & \dfrac{y_{1}}{2x_{1}}\left( x-x_{1}\right) \\ y & = & \dfrac{y_{1}}{2x_{1}}\left( x-x_{1}\right) +y_{1} \\ & = & y_{1}\left( \dfrac{x}{2x_{1}}-\dfrac{1}{2}+1\right) \\ & = & y_{1}\left( \dfrac{x}{2x_{1}}+\dfrac{1}{2}\right) \\ & = & \dfrac{y_{1}}{2}\left( \dfrac{x}{x_{1}}+1\right) . \end{eqnarray*} El punto de intersección de la recta tangente \(y=\dfrac{y_{1}}{2}\left( \dfrac{x}{x_{1}}+1\right) \) y la directriz \(x=-p\) es \begin{equation*} R\left( -p,\dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}}+1\right) \right) . \end{equation*} Despejamos \(y\) de la ecuación de la parábola \begin{eqnarray*} \left\vert y\right\vert & = & \sqrt{4px} \\ \left\vert y\right\vert & = & 2\sqrt{px}, \end{eqnarray*} de donde \begin{equation*} y=2\sqrt{px} \quad \quad \quad {\text o } \quad \quad \quad y=-2\sqrt{px}. \end{equation*}
La distancia del punto de tangencia \(P\left( x_{1},y_{1}\right) \) a \(S\left( -p,y_{1}\right) \) es \begin{eqnarray*} \sqrt{\left( x_{1}+p\right) ^{2}+\left( y_{1}-y_{1}\right) ^{2}} & = & \sqrt{ \left( x_{1}+p\right) ^{2}} \\ & = & \left\vert x_{1}+p\right\vert \\ & = & x_{1}+p \quad \quad \quad \text{ya que } x_{1}\geq 0 \text{ y } p>0 \end{eqnarray*} que corresponde al cateto \(PS\) del triángulo \(PSR.\)
La distancia de \(R\left( -p,\dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}} +1\right) \right) \) a \(S\left( -p,y_{1}\right) \) es \begin{eqnarray*} \sqrt{\left( -p+p\right) ^{2}+\left( \dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}} +1\right) -y_{1}\right) ^{2}} & = & \left\vert \dfrac{y_{1}}{2}\left( \dfrac{-p }{x_{1}}+1\right) -y_{1}\right\vert \\ & = & \left\vert y_{1}\left( \dfrac{-p}{2x_{1}}+\dfrac{1}{2}-1\right) \right\vert \\ & = & \left\vert y_{1}\left( \dfrac{-p}{2x_{1}}-\dfrac{1}{2}\right) \right\vert \\ & = & \left\vert -\dfrac{y_{1}}{2}\left( \dfrac{p}{x_{1}}+1\right) \right\vert \\ & = & \dfrac{y_{1}}{2}\left( \dfrac{p}{x_{1}}+1\right) \quad \quad \quad \text{ ya que } y_{1}>0 \end{eqnarray*} que corresponde al cateto \(RS\) del triángulo \(PSR.\)
El área del triángulo \(PSR\) es \begin{equation*} A=\dfrac{1}{2}\left( x_{1}+p\right) \left( \dfrac{y_{1}}{2}\left( \dfrac{p}{ x_{1}}+1\right) \right) . \end{equation*} Consideramos la función: \begin{eqnarray*} f\left( x,y\right) & = & \dfrac{1}{2}\left( x+p\right) \left( \dfrac{y}{2} \left( \dfrac{p}{x}+1\right) \right) \\ & = & \dfrac{py}{2}+\dfrac{xy}{4}+\dfrac{p^{2}y}{4x} \end{eqnarray*} y la restricción \begin{equation*} g\left( x,y\right) =y^{2}-4px=0. \end{equation*} Calculamos los gradientes de \(f\) y \(g\): \begin{eqnarray*} \dfrac{\partial f}{\partial x} & = & \dfrac{\partial }{\partial x}\left( \dfrac{ 1}{2}py+\dfrac{1}{4}xy+\dfrac{1}{4}\dfrac{p^{2}}{x}y\right) =-\dfrac{1}{ 4x^{2}}y\left( p^{2}-x^{2}\right) \\ \dfrac{\partial f}{\partial y} & = & \dfrac{\partial }{\partial y}\left( \dfrac{ 1}{2}py+\dfrac{1}{4}xy+\dfrac{1}{4}\dfrac{p^{2}}{x}y\right) =\dfrac{1}{4x} \left( p+x\right) ^{2} \end{eqnarray*} y \begin{equation*} \nabla g=\left( -4p,2y\right) . \end{equation*} De acuerdo con el método de Lagrange, debemos resolver el sistema de ecuaciones \begin{eqnarray*} -\dfrac{1}{4x^{2}}y\left( p^{2}-x^{2}\right) & = & -4p\lambda \\ \dfrac{1}{4x}\left( p+x\right) ^{2} & = & 2y\lambda \\ y^{2}-4px & = & 0. \end{eqnarray*} Despejando \(\lambda \) de la primera tenemos \begin{eqnarray*} \dfrac{1}{4p}\left( \dfrac{1}{4x^{2}}y\left( p^{2}-x^{2}\right) \right) & = & \lambda \\ \dfrac{y\left( p^{2}-x^{2}\right) }{16px^{2}} & = & \lambda \end{eqnarray*} y sustituyendo en la segunda ecuación del sistema, \begin{eqnarray*} \dfrac{1}{4x}\left( p+x\right) ^{2} & = & 2y\left( \dfrac{y\left( p^{2}-x^{2}\right) }{16px^{2}}\right) \\ \left( p+x\right) ^{2} & = & \dfrac{y^{2}\left( p^{2}-x^{2}\right) }{2px} \\ p+x & = & \dfrac{y^{2}\left( p-x\right) }{2px} \\ 2px\left( p+x\right) & = & y^{2}\left( p-x\right) \\ \dfrac{2px\left( p+x\right) }{p-x} & = & y^{2} \end{eqnarray*} y sustituyendo \(y^{2}\) en la tercera ecuación del sistema \begin{eqnarray*} y^{2}-4px & = & 0 \\ \dfrac{2px\left( p+x\right) }{p-x}-4px & = & 0 \\ 2px\left( p+x\right) -4px\left( p-x\right) & = & 0 \\ 2px\left( p+x-2\left( p-x\right) \right) & = & 0 \\ 2px\left( 3x-p\right) & = & 0 \end{eqnarray*} de donde, \begin{equation*} x=0 \quad \quad \quad \text{ o } \quad \quad \quad x=\dfrac{p}{3}. \end{equation*} Como \(x\) no puede ser cero, ya que en ese caso la primera derivada de \(f\) con respecto a \(x\) no está definida, entonces \(x=\dfrac{p}{3},\) de donde \begin{eqnarray*} y^{2} & = & 4p\left( \dfrac{p}{3}\right) \\ y^{2} & = & \dfrac{4}{3}p^{2} \\ \left\vert y\right\vert & = & \dfrac{2}{\sqrt{3}}p \\ y & = & \dfrac{2}{\sqrt{3}}p \quad \quad \quad \text{ ya que } y>0 \end{eqnarray*} y \begin{eqnarray*} \lambda & = & \dfrac{y\left( p^{2}-x^{2}\right) }{16px^{2}} \\ & = & \dfrac{\dfrac{2}{\sqrt{3}}p\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) }{16p\left( \dfrac{p}{3}\right) ^{2}} \\ & = & \dfrac{\dfrac{8}{9}p^{2}}{\sqrt{3}\left( 8\right) \dfrac{p^{2}}{9}} \\ & = & \dfrac{\sqrt{3}}{3}. \end{eqnarray*} El punto es \(\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}}p\right) \) y \(\lambda = \dfrac{\sqrt{3}}{3}.\) Consideramos la función \begin{equation*} h\left( x,y\right) =\dfrac{py}{2}+\dfrac{xy}{4}+\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) . \end{equation*} Calculamos \begin{eqnarray*} \dfrac{\partial h}{\partial x} & = & \dfrac{\partial }{\partial x}\left( \dfrac{ py}{2}+\dfrac{xy}{4}+\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) \right) =\dfrac{1}{4x^{2}}\left( -yp^{2}+16\lambda px^{2}+yx^{2}\right) \\ \dfrac{\partial h}{\partial y} & = & \dfrac{\partial }{\partial y}\left( \dfrac{ py}{2}+\dfrac{xy}{4}+\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) \right) =\dfrac{1}{4x}\left( p^{2}+2px+x^{2}-8y\lambda x\right) \end{eqnarray*} las de segundo orden \begin{eqnarray*} \dfrac{\partial ^{2}h}{\partial x^{2}} & = & \dfrac{\partial }{\partial x} \left( \dfrac{1}{4x^{2}}\left( -yp^{2}+16\lambda px^{2}+yx^{2}\right) \right) =\dfrac{p^{2}y}{2x^{3}} \\ \dfrac{\partial ^{2}h}{\partial y^{2}} & = & \dfrac{\partial }{\partial y} \left( \dfrac{1}{4x}\left( p^{2}+2px+x^{2}-8y\lambda x\right) \right) =-2\lambda \\ \dfrac{\partial ^{2}h}{\partial y\partial x} & = & \dfrac{\partial }{\partial y} \left( \dfrac{1}{4x^{2}}\left( -yp^{2}+16\lambda px^{2}+yx^{2}\right) \right) =-\dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) \\ \dfrac{\partial ^{2}h}{\partial x\partial y} & = & \dfrac{\partial }{\partial x} \left( \dfrac{1}{4x}\left( p^{2}+2px+x^{2}-8y\lambda x\right) \right) =- \dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) \end{eqnarray*} El hessiano es \begin{eqnarray*} \left\vert \overline{H}\left( x,y\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & \dfrac{\partial g}{\partial x}\left( x,y\right) & \dfrac{\partial g}{ \partial y}\left( x,y\right) \\ & & \\ \dfrac{\partial g}{\partial x}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x^{2}}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y\partial x}\left( x,y\right) \\ & & \\ \dfrac{\partial g}{\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y^{2}}\left( x,y\right) \end{array} \right\vert \\ && \\ & = & \left\vert \begin{array}{ccc} 0 & -4p & 2y \\ & & \\ -4p & \dfrac{p^{2}y}{2x^{3}} & -\dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) \\ & & \\ 2y & -\dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) & -2\lambda \end{array} \right\vert \end{eqnarray*} En el punto \(\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}}p\right) \) y \(\lambda = \dfrac{\sqrt{3}}{3}\) tenemos \begin{eqnarray*} \left\vert \overline{H}\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}}p\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & -4p & 2\left( \dfrac{2}{\sqrt{3}}p\right) \\ & & \\ -4p & \dfrac{p^{2}\left( \dfrac{2}{\sqrt{3}}p\right) }{2\left( \dfrac{p}{3} \right) ^{3}} & -\dfrac{1}{4\left( \dfrac{p}{3}\right) ^{2}}\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) \\ & & \\ 2\left( \dfrac{2}{\sqrt{3}}p\right) & -\dfrac{1}{4\left( \dfrac{p}{3}\right) ^{2}}\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) & -2\left( \dfrac{ \sqrt{3}}{3}\right) \end{array} \right\vert \\ & & \\ & = & \left\vert \begin{array}{ccc} 0 & -4p & \dfrac{4}{3}\sqrt{3}p \\ & & \\ -4p & 9\sqrt{3} & -2 \\ & & \\ \dfrac{4}{3}\sqrt{3}p & -2 & -\dfrac{2}{3}\sqrt{3} \end{array} \right\vert \\ && \\ & = & -16\sqrt{3}p^{2} < 0 \end{eqnarray*}
entonces, por el inciso 2 del Teorema 1, hay un mínimo en \(\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}} p\right) \) y su valor es \begin{equation*} f\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}}p\right) =\dfrac{p^{2}}{\sqrt{3}}+ \dfrac{p^{2}}{6\sqrt{3}}+\dfrac{3p^{2}}{2\sqrt{3}}=\frac{8}{9}\sqrt{3}p^{2} \end{equation*}
El punto de intersección de la recta tangente \(y=\dfrac{y_{1}}{2}\left( \dfrac{x}{x_{1}}+1\right) \) y la directriz \(x=-p\) es \begin{equation*} R\left( -p,\dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}}+1\right) \right) \end{equation*}
La ecuación de la recta perpendicular a la directriz \(x=-p\) desde el punto de tangencia \(P\left( x_{1},y_{1}\right) =P\left( x_{1},-2\sqrt{px_{1}} \right) \) es \begin{equation*} y=y_{1}=-2\sqrt{px_{1}} \end{equation*} y el punto de intersección de la directríz con esta recta es \begin{equation*} S\left( -p,y_{1}\right) \end{equation*} Así el triángulo \(PSR\) es rectángulo.
La distancia del punto de tangencia \(P\left( x_{1},y_{1}\right) \) a \(S\left( -p,y_{1}\right) \) es \begin{eqnarray*} \sqrt{\left( x_{1}+p\right) ^{2}+\left( y_{1}-y_{1}\right) ^{2}} & = & \sqrt{ \left( x_{1}+p\right) ^{2}} \\ & = & \left\vert x_{1}+p\right\vert \\ & = & x_{1}+p \quad \quad \quad \text{ya que } x_{1}\geq 0 \text{ y } p>0 \end{eqnarray*} que corresponde al cateto \(PS\) del triángulo \(PSR.\)
La distancia de \(R\left( -p,\dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}} +1\right) \right) \) a \(S\left( -p,y_{1}\right) \) es \begin{eqnarray*} \sqrt{\left( -p+p\right) ^{2}+\left( \dfrac{y_{1}}{2}\left( \dfrac{-p}{x_{1}} +1\right) -y_{1}\right) ^{2}} & = & \left\vert \dfrac{y_{1}}{2}\left( \dfrac{-p }{x_{1}}+1\right) -y_{1}\right\vert \\ & = & \left\vert y_{1}\left( \dfrac{-p}{2x_{1}}+\dfrac{1}{2}-1\right) \right\vert \\ & = & \left\vert y_{1}\left( \dfrac{-p}{2x_{1}}-\dfrac{1}{2}\right) \right\vert \\ & = & \left\vert -\dfrac{y_{1}}{2}\left( \dfrac{p}{x_{1}}+1\right) \right\vert \\ & = & -\dfrac{y_{1}}{2}\left( \dfrac{p}{x_{1}}+1\right) \quad \quad \quad \text{ ya que } y_{1} < 0 \end{eqnarray*}
que corresponde al cateto \(RS\) del triángulo \(PSR.\)
El área del triángulo \(PSR\) es \begin{equation*} A=\dfrac{1}{2}\left( x_{1}+p\right) \left( -\dfrac{y_{1}}{2}\left( \dfrac{p}{ x_{1}}+1\right) \right) . \end{equation*} Consideramos la función: \begin{eqnarray*} f\left( x,y\right) & = & \dfrac{1}{2}\left( x+p\right) \left( -\dfrac{y}{2} \left( \dfrac{p}{x}+1\right) \right) \\ & = & -\dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x} \end{eqnarray*} y la restricción \begin{equation*} g\left( x,y\right) =y^{2}-4px=0. \end{equation*} Calculamos los gradientes de \(f\) y \(g\): \begin{eqnarray*} \dfrac{\partial f}{\partial x} & = & \dfrac{\partial }{\partial x}\left( - \dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x}\right) =\dfrac{1}{4x^{2}} y\left( p^{2}-x^{2}\right) \\ \dfrac{\partial f}{\partial y} & = & \dfrac{\partial }{\partial y}\left( - \dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x}\right) =-\dfrac{1}{4x}\left( p+x\right) ^{2} \end{eqnarray*} y \begin{equation*} \nabla g=\left( -4p,2y\right) . \end{equation*} De acuerdo con el método de Lagrange, debemos resolver el sistema de ecuaciones \begin{eqnarray*} \dfrac{1}{4x^{2}}y\left( p^{2}-x^{2}\right) & = & -4p\lambda \\ -\dfrac{1}{4x}\left( p+x\right) ^{2} & = & 2y\lambda \\ y^{2}-4px & = & 0. \end{eqnarray*} Despejando \(\lambda \) de la primera tenemos \begin{eqnarray*} -\dfrac{1}{4p}\left( \dfrac{1}{4x^{2}}y\left( p^{2}-x^{2}\right) \right) & = & \lambda \\ -\dfrac{y\left( p^{2}-x^{2}\right) }{16px^{2}} & = & \lambda \end{eqnarray*} y sustituyendo en la segunda ecuación del sistema, \begin{eqnarray*} -\dfrac{1}{4x}\left( p+x\right) ^{2} & = & 2y\left( \dfrac{-y\left( p^{2}-x^{2}\right) }{16px^{2}}\right) \\ \left( p+x\right) ^{2} & = & \dfrac{y^{2}\left( p^{2}-x^{2}\right) }{2px} \\ p+x & = & \dfrac{y^{2}\left( p-x\right) }{2px} \\ 2px\left( p+x\right) & = & y^{2}\left( p-x\right) \\ \dfrac{2px\left( p+x\right) }{p-x} & = & y^{2} \end{eqnarray*} y sustituyendo \(y^{2}\) en la tercera ecuación del sistema \begin{eqnarray*} y^{2}-4px & = & 0 \\ \dfrac{2px\left( p+x\right) }{p-x}-4px & = & 0 \\ 2px\left( p+x\right) -4px\left( p-x\right) & = & 0 \\ 2px\left( p+x-2\left( p-x\right) \right) & = & 0 \\ 2px\left( 3x-p\right) & = & 0, \end{eqnarray*} de donde \begin{equation*} x=0 \quad \quad \quad \text{ o } \quad \quad \quad x=\dfrac{p}{3}. \end{equation*} Como \(x\) no puede ser cero, ya que en ese caso la primera derivada de \(f\) con respecto a \(x\) no está definida, entonces \(x=\dfrac{p}{3},\) de donde \begin{eqnarray*} y^{2} & = & 4p\left( \dfrac{p}{3}\right) \\ y^{2} & = & \dfrac{4}{3}p^{2} \\ \left\vert y\right\vert & = & \dfrac{2}{\sqrt{3}}p \\ y & = & -\dfrac{2}{\sqrt{3}}p \quad \quad \quad \text{ya que } y < 0 \end{eqnarray*}
y \begin{eqnarray*} \lambda & = & \dfrac{-y\left( p^{2}-x^{2}\right) }{16px^{2}} \\ & = & \dfrac{\dfrac{2}{\sqrt{3}}p\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) }{16p\left( \dfrac{p}{3}\right) ^{2}} \\ & = & \dfrac{\dfrac{8}{9}p^{2}}{\sqrt{3}\left( 8\right) \dfrac{p^{2}}{9}} \\ & = & \dfrac{\sqrt{3}}{3}. \end{eqnarray*} El punto es \(\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}}p\right) \) y \(\lambda = \dfrac{\sqrt{3}}{3}.\)
Consideramos la función \begin{equation*} h\left( x,y\right) =-\dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) . \end{equation*} Calculamos \begin{eqnarray*} \dfrac{\partial h}{\partial x} & = & \dfrac{\partial }{\partial x}\left( - \dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) \right) =\dfrac{1}{4x^{2}}\left( yp^{2}+16\lambda px^{2}-yx^{2}\right) \\ \dfrac{\partial h}{\partial y} & = & \dfrac{\partial }{\partial y}\left( - \dfrac{py}{2}-\dfrac{xy}{4}-\dfrac{p^{2}y}{4x}-\lambda \left( y^{2}-4px\right) \right) =-\dfrac{1}{4x}\left( p^{2}+2px+x^{2}+8y\lambda x\right) \end{eqnarray*} las de segundo orden \begin{eqnarray*} \dfrac{\partial ^{2}h}{\partial x^{2}} & = & \dfrac{\partial }{\partial x} \left( \dfrac{1}{4x^{2}}\left( yp^{2}+16\lambda px^{2}-yx^{2}\right) \right) =-\dfrac{p^{2}y}{2x^{3}} \\ \dfrac{\partial ^{2}h}{\partial y^{2}} & = & \dfrac{\partial }{\partial y} \left( -\dfrac{1}{4x}\left( p^{2}+2px+x^{2}+8y\lambda x\right) \right) =-2\lambda \\ \dfrac{\partial ^{2}h}{\partial y\partial x} & = & \dfrac{\partial }{\partial y} \left( \dfrac{1}{4x^{2}}\left( yp^{2}+16\lambda px^{2}-yx^{2}\right) \right) =\dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) \\ \dfrac{\partial ^{2}h}{\partial x\partial y} & = & \dfrac{\partial }{\partial x} \left( -\dfrac{1}{4x}\left( p^{2}+2px+x^{2}+8y\lambda x\right) \right) = \dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) . \end{eqnarray*} El hessiano es \begin{eqnarray*} \left\vert \overline{H}\left( x,y\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & \dfrac{\partial g}{\partial x}\left( x,y\right) & \dfrac{\partial g}{ \partial y}\left( x,y\right) \\ & & \\ \dfrac{\partial g}{\partial x}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x^{2}}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y\partial x}\left( x,y\right) \\ & & \\ \dfrac{\partial g}{\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y^{2}}\left( x,y\right) \end{array} \right\vert \\ & & \\ & = & \left\vert \begin{array}{ccc} 0 & -4p & 2y \\ & & \\ -4p & -\dfrac{p^{2}y}{2x^{3}} & \dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) \\ & & \\ 2y & \dfrac{1}{4x^{2}}\left( p^{2}-x^{2}\right) & -2\lambda \end{array} \right\vert \end{eqnarray*} En el punto \(\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}}p\right) \) y \(\lambda = \dfrac{\sqrt{3}}{3}\) tenemos \begin{eqnarray*} \left\vert \overline{H}\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}}p\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & -4p & 2\left( -\dfrac{2}{\sqrt{3}}p\right) \\ & & \\ -4p & -\dfrac{p^{2}\left( -\dfrac{2}{\sqrt{3}}p\right) }{2\left( \dfrac{p}{3} \right) ^{3}} & \dfrac{1}{4\left( \dfrac{p}{3}\right) ^{2}}\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) \\ & & \\ 2\left( -\dfrac{2}{\sqrt{3}}p\right) & \dfrac{1}{4\left( \dfrac{p}{3}\right) ^{2}}\left( p^{2}-\left( \dfrac{p}{3}\right) ^{2}\right) & -2\left( \dfrac{ \sqrt{3}}{3}\right) \end{array} \right\vert \\ & & \\ & = & \left\vert \begin{array}{ccc} 0 & -4p & -\dfrac{4}{3}\sqrt{3}p \\ & & \\ -4p & 9\sqrt{3} & 2 \\ & & \\ -\dfrac{4}{3}\sqrt{3}p & 2 & -\dfrac{2}{3}\sqrt{3} \end{array} \right\vert \\ && \\ & = & -16\sqrt{3}p^{2} < 0. \end{eqnarray*}
entonces, por el inciso 2 del Teorema 1, hay un mínimo en \(\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}} p\right) \) y su valor es \(\frac{7}{9}\sqrt{3}p^{2}\) \begin{equation*} f\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}}p\right) =-\dfrac{py}{2}-\dfrac{xy}{ 4}-\dfrac{p^{2}y}{4x}=\dfrac{p^{2}}{\sqrt{3}}+\dfrac{p^{2}}{6\sqrt{3}}+ \dfrac{3p^{2}}{2\sqrt{3}}. \end{equation*} Por tanto, en los puntos \(\left( \dfrac{p}{3},\dfrac{2}{\sqrt{3}}p\right) \) y \(\left( \dfrac{p}{3},-\dfrac{2}{\sqrt{3}}p\right) \) de la parábola \( y^{2}=4px,\) con \(p > 0,\) la tangentes a ésta, forman con la directriz y la perpendicular a la directriz desde el punto de tangencia, dos triángulos de la misma área mínima.