Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 1

Solución:

Sean \(s=\) altura, \(a=\) radio y \(V=\) volumen del cilindro buscado.

Así, \begin{equation*} V=\pi a^{2}s. \end{equation*} En la figura tenemos un corte transversal del cilindro inscrito en el cono

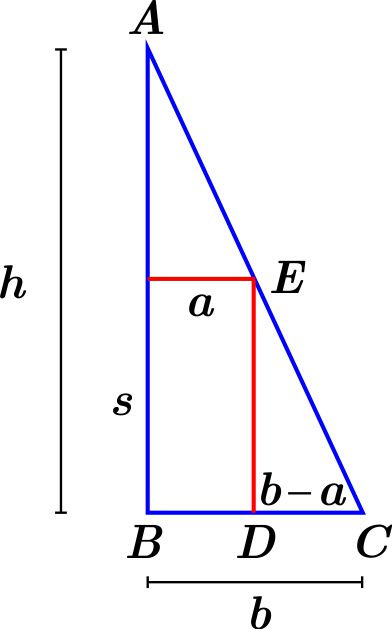
Tenemos \begin{equation*} \triangle ABC\approx \triangle EDC, \end{equation*} entonces \begin{equation*} \dfrac{b-a}{b}=\dfrac{s}{h}. \end{equation*} Definimos las funciones \begin{eqnarray*} f\left( a,s\right) & = & \pi a^{2}s \\ g\left( a,s\right) & = & \dfrac{b-a}{b}-\dfrac{s}{h}. \end{eqnarray*} Queremos maximizar \(f\) restringida a la condición \(g\left( a,s\right) =0. \) \begin{eqnarray*} \nabla f\left( a,s\right) & = & \left( \dfrac{\partial f}{\partial a},\dfrac{ \partial f}{\partial s}\right) =\left( 2\pi as,\pi a^{2}\right) \\ \nabla g\left( a,s\right) & = & \left( \dfrac{\partial g}{\partial a},\dfrac{ \partial g}{\partial s}\right) =\left( -\dfrac{1}{b},-\dfrac{1}{h}\right) . \end{eqnarray*} Consideramos el sistema \begin{eqnarray*} \nabla f\left( a,s\right) & = &\lambda \nabla g\left( a,s\right) \\ \dfrac{b-a}{b} & = &\dfrac{s}{h}, \end{eqnarray*} de donde: \begin{eqnarray} 2\pi as & = & -\dfrac{\lambda }{b} \label{1}\tag{1} \\ \pi a^{2} & = & -\dfrac{\lambda }{h} \notag \\ \dfrac{b-a}{b} & = & \dfrac{s}{h}. \notag \end{eqnarray} De la tercera ecuación de (\ref{1}) obtenemos: \begin{equation} s=\dfrac{\left( b-a\right) h}{b}. \label{1s}\tag{2} \end{equation} Sustituyendo en la primera: \begin{eqnarray*} 2\pi a\left( \dfrac{\left( b-a\right) h}{b}\right) & = & -\dfrac{\lambda }{b} \\ 2\pi a\left( b-a\right) h & = & -\lambda . \end{eqnarray*} Despejamos \(-\lambda \) de la segunda ecuación de (\ref{1}) y la sustituimos en la anterior: \begin{equation*} 2\pi a\left( b-a\right) h=h\pi a^{2}. \end{equation*} Simplificando \begin{eqnarray*} 2\left( b-a\right) & = & a \\ 2b-2a & = & a \\ 2b & = & 3a \\ a & = & \dfrac{2}{3}b. \end{eqnarray*} Sustituimos el valor de \(a\) en la expresión (\ref{1s}) que obtuvimos para \(s\): \begin{eqnarray*} s & = & \dfrac{\left( b-a\right) h}{b} \\ & = & \dfrac{\left( b-\dfrac{2}{3}b\right) h}{b} \\ & = & \dfrac{\left( \dfrac{1}{3}b\right) h}{b} \\ & = & \dfrac{1}{3}h. \end{eqnarray*} Por último, sustituyendo \(a=\dfrac{2}{3}b\) en la segunda ecuación de (\ref{1}): \(\pi a^{2}=-\dfrac{\lambda }{h}\), obtenemos \begin{eqnarray*} \pi \left( \dfrac{2}{3}b\right) ^{2} & = & -\dfrac{\lambda }{h} \\ \lambda & = & -\dfrac{4}{9}\pi hb^{2}. \end{eqnarray*} Entonces un punto en el que la función \(f\) puede tener un máximo o mínimo, es el punto de coordenadas \(\left( a,s\right) =\left( \dfrac{2}{3 }b,\dfrac{1}{3}h\right) \) y \(\lambda =-\dfrac{4}{9}\pi hb^{2}.\)

Usaremos el criterio del determinante hessiano límitado para saber si en el punto encontrado la función tiene un máximo o mínimo.

Definimos la función \begin{eqnarray*} h\left( a,s\right) & = & f\left( a,s\right) -\lambda g\left( a,s\right) \\ & = & \pi a^{2}s-\lambda \left( \dfrac{b-a}{b}-\dfrac{s}{h}\right) . \end{eqnarray*} Calculamos las derivadas de \(h\) hasta de orden \(2\): \begin{eqnarray*} \dfrac{\partial h }{\partial a}\left( a,s\right) & = & 2\pi as+\dfrac{\lambda }{ b} \\ \dfrac{\partial h }{\partial s}\left( a,s\right) & = & \pi a^{2}+\dfrac{\lambda }{h} \\ \dfrac{\partial ^{2}h }{\partial a^{2}} \left( a,s\right)& = & 2\pi s \\ \dfrac{\partial ^{2}h }{\partial s^{2}}\left( a,s\right) & = & 0 \\ \dfrac{\partial ^{2}h }{\partial a\partial s}\left( a,s\right) & = & 2\pi a= \dfrac{\partial ^{2}h }{\partial s\partial a}\left( a,s\right). \end{eqnarray*} Por otra parte, como \begin{equation*} \nabla g\left( a,s\right) =\left( \dfrac{\partial g}{\partial a},\dfrac{ \partial g}{\partial s}\right) =\left( -\dfrac{1}{b},-\dfrac{1}{h}\right) , \end{equation*} el determinante hessiano limitado es: \begin{equation*} \left\vert \overline{H}\left( a,s\right) \right\vert =\left\vert \begin{array}{ccc} 0 & \dfrac{\partial g}{\partial a}\left( a,s\right) & \dfrac{\partial g}{ \partial s}\left( a,s\right) \\ & & \\ \dfrac{\partial g}{\partial a}\left( a,s\right) & \dfrac{\partial ^{2}h}{ \partial a^{2}}\left( a,s\right) & \dfrac{\partial ^{2}h}{\partial s\partial a}\left( a,s\right) \\ & & \\ \dfrac{\partial g}{\partial s}\left( a,s\right) & \dfrac{\partial ^{2}h}{ \partial a\partial s}\left( a,s\right) & \dfrac{\partial ^{2}h}{\partial s^{2}}\left( a,s\right) \end{array} \right\vert =\left\vert \begin{array}{ccc} 0 & -\dfrac{1}{b} & -\dfrac{1}{h} \\ & & \\ -\dfrac{1}{b} & 2\pi s & 2\pi a \\ & & \\ -\dfrac{1}{h} & 2\pi a & 0 \end{array} \right\vert \end{equation*} Evaluando en el punto de coordenadas \(\left( \dfrac{2}{3}b,\dfrac{1}{3} h\right) ,\) obtenemos \begin{equation*} \left\vert \overline{H}\left( \dfrac{2}{3}b,\dfrac{1}{3}h\right) \right\vert =\left\vert \begin{array}{ccc} 0 & -\dfrac{1}{b} & -\dfrac{1}{h} \\ & & \\ -\dfrac{1}{b} & \dfrac{2\pi }{3}h & \dfrac{4\pi }{3}b \\ & & \\ -\dfrac{1}{h} & \dfrac{4\pi }{3}b & 0 \end{array} \right\vert =\dfrac{2\pi }{h}>0 \quad \text{ ya que } h>0. \end{equation*} Así, por el inciso 1 del Teorema 1, \(\left( \dfrac{2}{3}b,\dfrac{1}{3}h\right) \) es un punto máximo relativo de \(f\) bajo la restricción \(g\left( a,s\right) =\dfrac{b-a }{b}-\dfrac{s}{h}=0\). Por tanto, el cilindro de mayor volumen que se puede inscribir en el cono circular recto de altura \(h\) y radio de la base \(b,\) es el que tiene altura \( s=\dfrac{1}{3}h\) y radio de la base \(a=\dfrac{2}{3}b\) y su volumen es \begin{equation*} V=\pi a^{2}s=\pi \left( \dfrac{2}{3}b\right) ^{2}\left( \dfrac{1}{3}h\right) =\dfrac{4}{27}\pi b^{2}h. \end{equation*}