Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 7

Solución:

Como las derivadas parciales de la función existen en todo el plano, entonces los valores extremos se pueden alcanzar en

• el interior de la región, en los puntos estacionarios o
• los puntos frontera de la región.

• Puntos estacionarios:

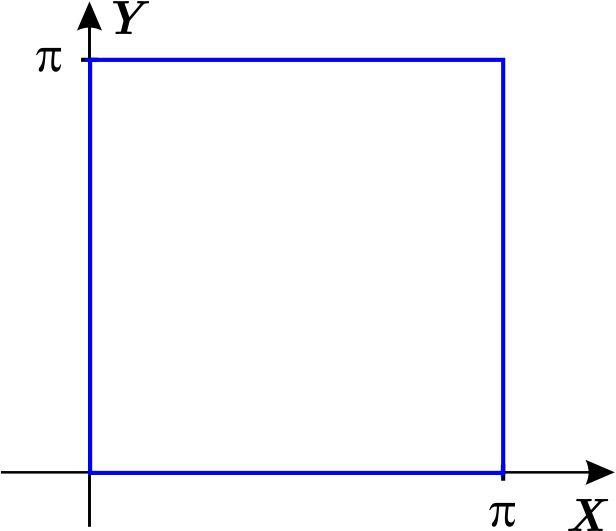
  La función es \begin{equation*} f\left( x,y\right) =\cos x+\cos y+\cos \left( x+y\right) \end{equation*} Calculamos las derivadas parciales \begin{equation*} \dfrac{\partial f}{\partial x}=- \text{sen}\ x- \text{sen}\ \left( x+y\right) \quad \quad \quad \text{ y } \quad \quad \quad \dfrac{\partial f}{ \partial y}=- \text{sen}\ y- \text{sen}\ \left( x+y\right) \end{equation*} las igualamos a cero \begin{eqnarray} - \text{sen}\ x- \text{sen}\ \left( x+y\right) & = & 0 \label{parciconsen}\tag{1} \\ - \text{sen}\ y- \text{sen}\ \left( x+y\right) & = & 0 \notag \end{eqnarray} de donde \begin{eqnarray*} - \text{sen}\ x & = & - \text{sen}\ y \\ \text{sen}\ x & = & \text{sen}\ y \\ \text{sen}\ x- \text{sen}\ y & = & 0 \\ 2\cos \left( \dfrac{x+y}{2}\right) \text{sen}\ \left( \dfrac{x-y}{2}\right) & = & 0 \end{eqnarray*} así \begin{equation*} \cos \left( \dfrac{x+y}{2}\right) =0 \quad \quad \quad \text{ o } \quad \quad \quad \text{sen}\ \left( \dfrac{x-y}{2}\right) =0 \end{equation*} es decir \begin{equation*} \dfrac{x+y}{2}=\dfrac{\pi }{2}, \quad \quad \quad \dfrac{x-y}{2}=\pi \quad \quad \quad \text{ o } \quad \quad \quad \dfrac{x-y}{2}=0 \end{equation*} de donde \begin{equation*} x+y=\pi , \quad \quad \quad x-y=2\pi \quad \quad \quad \text{ o } \quad \quad \quad x-y=0 \end{equation*} Entonces tenemos \begin{equation*} y=x+\pi ,\quad \quad \quad y=x-2\pi \quad \quad \quad \text{ o } \quad \quad \quad x=y \end{equation*}

  • Si $y=x+\pi ,$ como $x\in \left[ 0,\pi \right] $ \begin{eqnarray*} 0 &\leq &x\leq \pi \\ \pi &\leq &x+\pi \leq \pi +\pi \\ \pi &\leq &y\leq 2\pi \end{eqnarray*} pero,por hipótesis, $y\in \left[ 0,\pi \right] ,$ entonces este caso no puede darse.
  • Si $y=x-2\pi ,$ como $x\in \left[ 0,\pi \right] $ \begin{eqnarray*} 0 &\leq &x\leq \pi \\ -2\pi &\leq &x-2\pi \leq \pi -2\pi \\ -2\pi &\leq &y\leq -\pi \end{eqnarray*} pero,por hipótesis, $y\in \left[ 0,\pi \right] ,$ entonces este caso no puede darse.
  • Si $y=x,$ entonces al sustituir $y$ por $x$ en cualquiera de las ecuaciones en (\ref{parciconsen}), obtenemos \begin{eqnarray*} \text{sen}\ x+ \text{sen}\ \left( 2x\right) & = & 0 \\ \text{sen}\ x+2 \text{sen}\ x\cos x & = & 0 \\ \text{sen}\ x\left( 1+2\cos x\right) & = & 0 \end{eqnarray*} De donde \begin{equation*} \text{sen}\ x=0 \quad \quad \quad \text{ o } \quad \quad \quad 1+2\cos x=0 \end{equation*} Si $ \text{sen}\ x=0,$ entonces \begin{equation*} x=0 \quad \quad \quad \text{ o } \quad \quad \quad x=\pi . \end{equation*} y obtenemos los puntos $\left( 0,0\right) $ y $\left( 0,\pi \right) $ que no están en el interior de la región considerada.

    Si $1+2\cos x=0,$ entonces \begin{eqnarray*} 1+2\cos x & = & 0 \\ \cos x & = & -\dfrac{1}{2} \\ x & = & \dfrac{2\pi }{3} \end{eqnarray*}

    O sea, tenemos el punto $A\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) $ que sí está en el interior de la región y como en él se anulan las derivadas parciales de $f,$ se trata de un punto estacionario de esta función.

    

    Calculamos las derivadas parciales de segundo orden de $f$ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}} & = & -\cos x-\cos \left( x+y\right) \\ \dfrac{\partial ^{2}f}{\partial x\partial y} & = & -\cos \left( x+y\right) = \dfrac{\partial ^{2}f}{\partial y\partial x} \\ \dfrac{\partial ^{2}f}{\partial y^{2}} & = & -\cos y-\cos \left( x+y\right) \end{eqnarray*}

    y las evaluamos en $A\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3 }\right) & = & -\cos \dfrac{2\pi }{3}-\cos \left( \dfrac{4\pi }{3}\right) =1>0 \\ \dfrac{\partial ^{2}f}{\partial x\partial y} & = & \dfrac{\partial ^{2}f}{ \partial y\partial x}=-\cos \left( \dfrac{4\pi }{3}\right) =\frac{1}{2} \\ \dfrac{\partial ^{2}f}{\partial y^{2}} & = & -\cos \dfrac{2\pi }{3}-\cos \left( \dfrac{4\pi }{3}\right) =1. \end{eqnarray*} El determinante hessiano en $A\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) $ es \begin{equation*} \left\vert \overline{H}\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) \right\vert =\left\vert \begin{array}{ccc} 1 & & \dfrac{1}{2} \\ & & \\ \dfrac{1}{2} & & 1 \end{array} \right\vert =\frac{3}{4}>0. \end{equation*} Por tanto, en $A\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) $ la función tiene un mínimo relativo estricto.

• Los puntos frontera son los que están en el cuadrado. Las ecuaciones de los lados del cuadrado son \begin{equation*} \left\{ \begin{array}{lcc} x=0 & & \text{con }0\leq y\leq \pi \\ x=\pi & & \text{con }0\leq y\leq \pi \\ y=0 & & \text{con }0\leq x\leq \pi \\ y=\pi & & \text{con }0\leq x\leq \pi \end{array} \right. \end{equation*} Evaluamos la función $f\left( x,y\right) =\cos x+\cos y+\cos \left( x+y\right) $ en los puntos de cada lado del cuadrado.
  • Si $x=0,$ entonces \begin{equation*} f\left( 0,y\right) =\cos 0+\cos y+\cos y=1+2\cos y \end{equation*} con $0\leq y\leq \pi .$ Los valores extremos de $f\left( 0,y\right) $ se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ 0,\pi \right] $: $0$ y $\pi,$ que corresponden a $B\left( 0,0\right)$ y $C\left( 0,\pi \right)$ Ahí los valores de $f\left( 0,y\right) =1+2\cos y$ son \begin{eqnarray*} f\left( 0,0\right) & = & 3 \\ f\left( 0,\pi \right) & = & -1; \end{eqnarray*}

    (ii) En los puntos interiores del intervalo $\left[ 0,\pi \right] $ donde la derivada se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dy}\left( 0,y\right) =-2 \text{sen}\ y \end{equation*} y la igualamos a cero, para encontrar el valor de $y$ \begin{equation*} -2 \text{sen}\ y=0, \end{equation*} es decir, \begin{equation*} y=0 \quad \quad \quad \text{ o } \quad \quad \quad y=\pi \end{equation*} pero los dos valores obtenidos son los extremos del intervalo, así que no hay ningún punto en el interior del intervalo donde la función alcance un máximo o un mínimo.

  • Si $x=\pi ,$ entonces \begin{equation*} f\left( \pi ,y\right) =\cos \pi +\cos y+\cos \left( \pi +y\right) =-1+\cos y-\cos y=-1 \end{equation*} con $0\leq y\leq \pi .$ Al tratarse de una función constante, $f$ restringida a este lado tiene en cada punto $\left( \pi ,y\right) $ un valor máximo y mínimo: $-1$.
  • Si $y=0,$ entonces \begin{equation*} f\left( x,0\right) =\cos x+\cos 0+\cos x=2\cos x+1 \end{equation*} con $0\leq x\leq \pi.$ Los valores extremos de $f\left( 0,y\right) $ se pueden alcanzar en $0$ o en:

    (i) Los extremos del intervalo $\left[ 0,\pi \right] $: $0$ y $\pi,$ que corresponden a $B\left( 0,0\right)$, que ya habíamos considerado, y $D\left( \pi ,0\right)$ Ahí los valores de $f\left( x,0\right) =2\cos x+1$ son \begin{eqnarray*} f\left( 0,0\right) & = & 3 \\ f\left( \pi ,0\right) & = & -1; \end{eqnarray*}

    (ii) Los puntos interiores del intervalo $\left[ 0,\pi \right] $ donde la derivada se anula.

    Este caso es análogo al caso en el que $x=0.$

  • Si $y=\pi ,$ entonces \begin{equation*} f\left( x,\pi \right) =\cos x+\cos \pi -\cos x=-1 \end{equation*} con $0\leq x\leq \pi .$ Este caso es análogo al caso en el que $x=\pi .$

Los valores de la función obtenidos en los puntos que son candidatos a ser máximo o mínimo absolutos son: \begin{equation*} \begin{array}{cccccc} f\left( 0,0\right) =3 & & & f\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3} \right) =-\dfrac{3}{2} & & f\left( 0,\pi \right) =-1 \\ & & & & & \\ f\left( \pi ,\pi \right) =-1 & & & f\left( \pi ,0\right) =-1 & & \end{array} \end{equation*} Entonces en el punto $A\left( \dfrac{2\pi }{3},\dfrac{2\pi }{3}\right) $ la función $f(x,y)$ alcanza el valor mínimo absoluto: $-\dfrac{3}{2}$ y en el punto $B\left( 0,0\right) $ la función $f(x,y)$ alcanza el valor máximo absoluto: $0.$