Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 5

Solución:

La función es polinomial, por lo que las derivadas parciales existen en todo el plano, entonces los valores extremos se pueden alcanzar en

• el interior de la región, en los puntos estacionarios. o
• los puntos frontera de la región.

La región es

• Puntos estacionarios: La función es \begin{eqnarray*} f\left( x,y\right) & = & xy\left( x^{2}+y^{2}-1\right) \\ & = & x^{3}y+xy^{3}-xy. \end{eqnarray*} Calculamos las derivadas parciales \begin{equation*} \dfrac{\partial f}{\partial x}=3x^{2}y+y^{3}-y \quad \quad \quad \text{ y } \quad \quad \quad \dfrac{\partial f}{\partial y}=x^{3}+3xy^{2}-x. \end{equation*} Las igualamos a cero para encontrar los puntos estacionarios \begin{eqnarray*} 3x^{2}y+y^{3}-y & = & 0 \\ x^{3}+3xy^{2}-x & = & 0. \end{eqnarray*} Podemos escribir este sistema como \begin{eqnarray} y\left( 3x^{2}+y^{2}-1\right) & = & 0 \label{ejer5} \\ x\left( x^{2}+3y^{2}-1\right) & = & 0 \notag \end{eqnarray}
  • Si $y=0,$ entonces \begin{eqnarray*} x\left( x^{2}-1\right) & = & 0 \\ x\left( x-1\right) \left( x+1\right) & = & 0, \end{eqnarray*} de donde \begin{equation*} x=0, \quad \quad \quad x=1, \quad \quad \quad x=-1. \end{equation*} Entonces hay tres soluciones $\left( 0,0\right) ,$ $\left( 1,0\right) ,$ $ \left( -1,0\right) .$
  • Si $x=0,$ entonces \begin{eqnarray*} y\left( y^{2}-1\right) & = & 0 \\ y\left( y-1\right) \left( y+1\right) & = & 0 \end{eqnarray*} de donde \begin{equation*} y=0, \quad \quad \quad y=1, \quad \quad \quad y=-1. \end{equation*} Entonces hay tres soluciones $\left( 0,0\right) ,$ $\left( 0,1\right) ,$ $ \left( 0,-1\right) .$
  • Si $x\neq 0$ y $y\neq 0,$ entonces \begin{eqnarray*} 3x^{2}+y^{2}-1 & = & 0 \\ x^{2}+3y^{2}-1 & = & 0. \end{eqnarray*} Multiplicamos la segunda ecuación por $-3$ \begin{eqnarray*} 3x^{2}+y^{2}-1 & = & 0 \\ -3x^{2}-9y^{2}+3 & = & 0 \end{eqnarray*} y las sumamos \begin{eqnarray*} -8y^{2}+2 & = & 0 \\ y^{2} & = & \dfrac{1}{4} \\ \left\vert y\right\vert & = & \dfrac{1}{2}, \end{eqnarray*} de donde, \begin{equation*} y=\dfrac{1}{2} \quad \quad \quad \text{ o } \quad \quad \quad y=-\dfrac{1}{2}. \end{equation*} Sustituyendo cualquiera de estos valores en la primera ecuación tenemos \begin{eqnarray*} 3x^{2}+\dfrac{1}{4}-1 & = & 0 \\ 3x^{2}-\dfrac{3}{4} & = & 0 \\ x^{2} & = & \dfrac{1}{4} \\ \left\vert x\right\vert & = & \dfrac{1}{2}, \end{eqnarray*} de donde, \begin{equation*} x=\dfrac{1}{2} \quad \quad \quad \text{ o }\quad \quad \quad x=-\dfrac{1}{2}. \end{equation*} Entonces los puntos $\left( \dfrac{1}{2},\dfrac{1}{2}\right) ,$ $\left( \dfrac{1}{2},-\dfrac{1}{2}\right) ,$ $\left( -\dfrac{1}{2},\dfrac{1}{2} \right) ,$ $\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) $ son estacionarios.

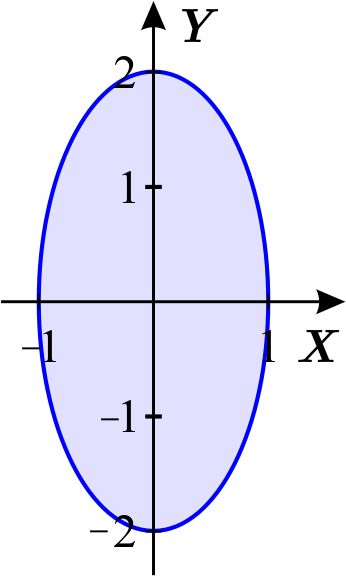
  Observamos que de todos estos puntos sólo $A\left( 0,0\right) ,$ $B\left( 0,1\right) ,$ $C\left( 0,-1\right) ,$ $D\left( -\dfrac{1}{2},\dfrac{1}{2} \right) ,$ $E\left( \dfrac{1}{2},-\dfrac{1}{2}\right) ,$ $F\left( \dfrac{1}{2}, \dfrac{1}{2}\right) ,$ $G\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) $ están dentro de la elipse. En tanto que los puntos $\left( -1,0\right) $ y $ \left( 1,0\right) $ están sobre la elipse. Por tanto, sólo los siete primeros son estacionarios en el interior de la región elíptica.

  

  Calculamos las derivadas parciales de segundo orden de la función $f\left( x,y\right) =x^{3}y+xy^{3}-xy$. Recordemos que \begin{eqnarray*} \dfrac{\partial f}{\partial x} & = & 3x^{2}y+y^{3}-y \\ \dfrac{\partial f}{\partial y} & = & x^{3}+3xy^{2}-x, \end{eqnarray*} entonces \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}=6xy \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y\partial x}=3x^{2}+3y^{2}-1 \quad \quad \quad \dfrac{ \partial ^{2}f}{\partial y^{2}}=6xy \end{equation*} y el determinante hessiano es \begin{equation*} \left\vert H\left( x,y\right) \right\vert =36x^{2}y^{2}-\left( 3x^{2}+3y^{2}-1\right) ^{2}. \end{equation*}

  • En $\left( 0,0\right) $ \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,0\right) =0 \quad \quad \quad \left\vert H\left( 0,0\right) \right\vert =-1 < 0, \end{equation*}

    de donde $\left( 0,0\right) $ es un punto silla.

  • En $\left( 0,1\right) $ \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,1\right) =0 \quad \quad \quad \left\vert H\left( 0,1\right) \right\vert =-\left( 3-1\right) ^{2}=-4 < 0, \end{equation*}

    así en $\left( 0,1\right) $ hay un punto silla.

  • En $\left( 0,-1\right) $ \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,-1\right) =0 \quad \quad \quad \left\vert H\left( 0,-1\right) \right\vert =-4 < 0. \end{equation*}

    Entonces en $\left( 0,-1\right) $ hay un punto silla. Recordemos que \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}=6xy \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y\partial x}=3x^{2}+3y^{2}-1 \quad \quad \quad \dfrac{ \partial ^{2}f}{\partial y^{2}}=6xy \end{equation*} y el determinante hessiano es \begin{equation*} \left\vert H\left( x,y\right) \right\vert =36x^{2}y^{2}-\left( 3x^{2}+3y^{2}-1\right) ^{2}. \end{equation*}

  • En $\left( \dfrac{1}{2},\dfrac{1}{2}\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( \dfrac{1}{2},\dfrac{1}{2} \right) & = & \dfrac{3}{2}>0 \\ \left\vert H\left( \dfrac{1}{2},\dfrac{1}{2}\right) \right\vert & = & 2 > 0. \end{eqnarray*} Entonces en $\left( \dfrac{1}{2},\dfrac{1}{2}\right) $ hay un mínimo relativo y ahí la función vale \begin{equation*} f\left( \dfrac{1}{2},\dfrac{1}{2}\right) =-\dfrac{1}{8}. \end{equation*}
  • En $\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -\dfrac{1}{2},-\dfrac{1}{2} \right) & = & \dfrac{3}{2}>0 \\ \left\vert H\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) \right\vert & = & 2>0. \end{eqnarray*} Entonces en $\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) $ hay un mínimo relativo y \begin{equation*} f\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) =-\dfrac{1}{8}. \end{equation*}
  • En $\left( -\dfrac{1}{2},\dfrac{1}{2}\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -\dfrac{1}{2},\dfrac{1}{2} \right) & = & -\dfrac{3}{2}<0 \\ \left\vert H\left( -\dfrac{1}{2},\dfrac{1}{2}\right) \right\vert & = & 2>0. \end{eqnarray*} Entonces en $\left( -\dfrac{1}{2},\dfrac{1}{2}\right) $ hay un máximo relativo y ahí la función vale \begin{equation*} f\left( -\dfrac{1}{2},\dfrac{1}{2}\right) =\dfrac{1}{8}. \end{equation*}
  • En $\left( \dfrac{1}{2},-\dfrac{1}{2}\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( \dfrac{1}{2},-\dfrac{1}{2} \right) & = & -\dfrac{3}{2}<0 \\ \left\vert H\left( \dfrac{1}{2},-\dfrac{1}{2}\right) \right\vert & = & 2 > 0. \end{eqnarray*} Entonces en $\left( \dfrac{1}{2},-\dfrac{1}{2}\right) $ hay un máximo relativo y ahí la función vale \begin{equation*} f\left( \dfrac{1}{2},-\dfrac{1}{2}\right) =\dfrac{1}{8}. \end{equation*}
  Por lo tanto, \[ \begin{array}{cc} \text{Puntos silla} & \left( 0,0\right) ,\left( 0,1\right) ,\left( 0,-1\right) \\ & \\ \text{Puntos máximos} & \left( -\dfrac{1}{2},\dfrac{1}{2}\right) ,\left( \dfrac{1}{2},-\dfrac{1}{2}\right) \\ & \\ \text{Puntos mínimos} & \left( \dfrac{1}{2},\dfrac{1}{2}\right) ,\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) .% \end{array}% \]
• Los puntos frontera son los que están sobre la elipse.

  Despejamos $y$ de la ecuación de la elipse $x^{2}+\dfrac{y^{2}}{4}=1$ \begin{eqnarray*} y^{2} & = & 4\left( 1-x^{2}\right) \\ \left\vert y\right\vert & = & \sqrt{4\left( 1-x^{2}\right) } \\ \left\vert y\right\vert & = & 2\sqrt{1-x^{2}} \end{eqnarray*} de donde \begin{equation*} y=2\sqrt{1-x^{2}} \quad \quad \quad \text{ o } \quad \quad \quad y=-2\sqrt{ 1-x^{2}} \end{equation*} Recordemos que $f\left( x,y\right) =xy\left( x^{2}+y^{2}-1\right) .$

  • Si $y=2\sqrt{1-x^{2}},$ entonces \begin{equation*} f\left( x,2\sqrt{1-x^{2}}\right) =6x\left( 1-x^{2}\right) ^{\frac{3}{2}} \end{equation*} con $-1\leq x\leq 1$. Los valores extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -1,1\right] $: $-1$ y $1$. Ahí los valores de $f\left( x,2\sqrt{1-x^{2}}\right) $ son \begin{eqnarray*} f\left( -1,0\right) & = & 0 \\ f\left( 1,0\right) & = & 0; \end{eqnarray*}

    (ii) Los puntos del interior de $\left[ -1,1\right] $ donde la derivada \begin{equation*} \dfrac{df}{dx}\left( x,2\sqrt{1-x^{2}}\right) =6\left( 1-x^{2}\right) ^{ \frac{1}{2}}\left( 1-4x^{2}\right) \end{equation*} se anula, o sea \begin{equation*} 6\left( 1-x^{2}\right) ^{\frac{1}{2}}\left( 1-4x^{2}\right) =0. \end{equation*} Esto equivale a \begin{equation*} 6\left( 1-x^{2}\right) ^{\frac{1}{2}}=0 \quad \quad \quad \text{ o } \quad \quad \quad 1-4x^{2}=0, \end{equation*} de donde, \begin{equation*} x=-1, \quad \quad x=1, \quad \quad x=-\dfrac{1}{2}, \quad \quad x=\dfrac{1}{2} \end{equation*} Los casos $x=-1,$ $x=1$ no se consideran pues no están en el interior de $\left[ -1,1\right] .$

    Calculamos la segunda derivada de $f\left( x,2\sqrt{1-x^{2}}\right) $ \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( x,2\sqrt{1-x^{2}}\right) =\dfrac{d}{dx}\left( 6\left( 1-x^{2}\right) ^{\frac{1}{2}}\left( 1-4x^{2}\right) \right) =\dfrac{ 18x\left( 4x^{2}-3\right) }{\left( 1-x^{2}\right) ^{\frac{1}{2}}}. \end{equation*}

    Si $x=-\dfrac{1}{2},$ entonces $y=2\sqrt{1-\left( -\dfrac{1}{2}\right) ^{2}} =\sqrt{3}\ $y \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( -\dfrac{1}{2},\sqrt{3}\right) =\dfrac{18\left( - \dfrac{1}{2}\right) \left( 1-3\right) }{\left( \dfrac{3}{4}\right) ^{\frac{1 }{2}}}=12\sqrt{3}>0, \end{equation*} así $f\left( x,2\sqrt{1-x^{2}}\right) $ tiene un mínimo relativo en $-\dfrac{1}{2}$ y su valor es \begin{equation*} f\left( -\dfrac{1}{2},\sqrt{3}\right) =6\left( -\dfrac{1}{2}\right) \left( \dfrac{3}{4}\right) ^{\frac{3}{2}}=-\dfrac{9}{8}\sqrt{3}\approx -1.95. \end{equation*} Si $x=\dfrac{1}{2},$ entonces $y=2\sqrt{1-\left( \dfrac{1}{2}\right) ^{2}}= \sqrt{3}\ $y \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( \dfrac{1}{2},\sqrt{3}\right) =\dfrac{18\left( \dfrac{1}{2}\right) \left( 1-3\right) }{\left( \dfrac{3}{4}\right) ^{\frac{1 }{2}}}=-12\sqrt{3} < 0, \end{equation*}

    de donde, $f\left( x,2\sqrt{1-x^{2}}\right) $ tiene un máximo relativo en $\dfrac{1}{2}$ y su valor es \begin{equation*} f\left( \dfrac{1}{2},\sqrt{3}\right) =6\left( \dfrac{1}{2}\right) \left( \dfrac{3}{4}\right) ^{\frac{3}{2}}=\dfrac{9}{8}\sqrt{3}\approx 1.95. \end{equation*} Por lo tanto, \begin{equation*} \begin{array}{ll} \text{Punto máximo:} & \left( \dfrac{1}{2},\sqrt{3}\right) \\ & \\ \text{Punto mínimo:} & \left( -\dfrac{1}{2},\sqrt{3}\right) . \end{array} \end{equation*}

  • Si $y=-2\sqrt{1-x^{2}},$ entonces \begin{equation*} f\left( x,-2\sqrt{1-x^{2}}\right) =-6x\left( 1-x^{2}\right) ^{\frac{3}{2}} \end{equation*} con $-1\leq x\leq 1$. Los valores extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -1,1\right] $: $-1$ y $1.$ Ahí los valores de $f\left( x,-2\sqrt{1-x^{2}}\right) $ son \begin{eqnarray*} f\left( -1,0\right) & = & 0 \\ f\left( 1,0\right) & = & 0; \end{eqnarray*}

    (ii ) Los puntos del interior de $\left[ -1,1\right] $ donde la derivada \begin{equation*} \dfrac{df}{dx}\left( x,-2\sqrt{1-x^{2}}\right) =-6\left( 1-x^{2}\right) ^{ \frac{1}{2}}\left( 1-4x^{2}\right) \end{equation*} se anula, o sea, \begin{equation*} -6\left( 1-x^{2}\right) ^{\frac{1}{2}}\left( 1-4x^{2}\right) =0 \end{equation*} que equivale a \begin{equation*} -6\left( 1-x^{2}\right) ^{\frac{1}{2}}=0 \quad \quad \quad \text{ o } \quad \quad \quad 1-4x^{2}=0, \end{equation*} de donde, \begin{equation*} x=-1, \quad \quad x=1, \quad \quad x=-\dfrac{1}{2}, \quad \quad x=\dfrac{1}{2}. \end{equation*} Los casos $x=-1,$ $x=1$ no se consideran pues no están en el interior de $\left[ -1,1\right] .$

    Calculamos la segunda derivada \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( x,-2\sqrt{1-x^{2}}\right) =\dfrac{-18x\left( 4x^{2}-3\right) }{\left( 1-x^{2}\right) ^{\frac{1}{2}}}. \end{equation*} Si $x=-\dfrac{1}{2},$ entonces $y=-2\sqrt{1-\left( -\dfrac{1}{2}\right) ^{2}} =-\sqrt{3}$ y \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( -\dfrac{1}{2},-\sqrt{3}\right) =\dfrac{ -18\left( -\dfrac{1}{2}\right) \left( 1-3\right) }{\left( \dfrac{3}{4} \right) ^{\frac{1}{2}}}=-12\sqrt{3} < 0, \end{equation*}

    de donde, $f\left( x,-2\sqrt{1-x^{2}}\right) $ tiene un máximo relativo en $-\dfrac{1}{2}$ y su valor es: \begin{equation*} f\left( -\dfrac{1}{2},-\sqrt{3}\right) =\dfrac{9}{8}\sqrt{3} \end{equation*} Si $x=\dfrac{1}{2},$ entonces $y=-2\sqrt{1-\left( \dfrac{1}{2}\right) ^{2}}=- \sqrt{3}$ y \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( \dfrac{1}{2},-\sqrt{3}\right) =12\sqrt{3}>0, \end{equation*} de donde, $f\left( x,-2\sqrt{1-x^{2}}\right) $ tiene un mínimo relativo en $\dfrac{1}{\sqrt{3}}$ y su valor es \begin{equation*} f\left( \dfrac{1}{2},-\sqrt{3}\right) =-\dfrac{9}{8}\sqrt{3}. \end{equation*} Por lo tanto, \begin{equation*} \begin{array}{ll} \text{Punto máximo:} & \left( -\dfrac{1}{2},-\sqrt{3}\right) \\ & \\ \text{Punto mínimo:} & \left( \dfrac{1}{2},-\sqrt{3}\right) . \end{array} \end{equation*}

Los valores de la función obtenidos en los puntos que son candidatos a ser máximo o mínimo absolutos son: \begin{equation*} \begin{array}{lll} f\left( \dfrac{1}{2},\dfrac{1}{2}\right) =-\dfrac{1}{8} & f\left( -1,0\right) =0 & f\left( 1,0\right) =0 \\ & & \\ f\left( -\dfrac{1}{2},-\dfrac{1}{2}\right) =-\dfrac{1}{8} & f\left( -\dfrac{1 }{2},\sqrt{3}\right) =-\dfrac{9}{8}\sqrt{3}\approx -1.95 & f\left( \dfrac{1}{ 2},-\dfrac{1}{2}\right) =\dfrac{1}{8} \\ & & \\ f\left( -\dfrac{1}{2},\dfrac{1}{2}\right) =\dfrac{1}{8} & f\left( -\dfrac{1}{ 2},-\sqrt{3}\right) =\dfrac{9}{8}\sqrt{3}\approx 1.95 & f\left( \dfrac{1}{2}, \sqrt{3}\right) =\dfrac{9}{8}\sqrt{3} \\ & & \\ f\left( \dfrac{1}{2},-\sqrt{3}\right) =-\dfrac{9}{8}\sqrt{3}. & & \end{array} \end{equation*} Entonces en los puntos $\left( \dfrac{1}{2},-\sqrt{3}\right) $ y $\left( - \dfrac{1}{2},\sqrt{3}\right) $ la función $f(x,y)$ alcanza el valor m ínimo absoluto: $-\dfrac{9}{8}\sqrt{3}$ y en los puntos $\left( -\dfrac{ 1}{2},-\sqrt{3}\right) $ y $\left( \dfrac{1}{2},\sqrt{3}\right) $ la funci ón $f(x,y)$ alcanza el valor máximo absoluto: $\dfrac{9}{8}\sqrt{3}.$

• Otra manera de encontrar los valores extremos en la frontera. Vamos a utilizar el método de multiplicadores de Lagrange.

  Consideramos la función $f\left( x,y\right) =x^{3}y+xy^{3}-xy$ con la restricción $g\left( x,y\right) =x^{2}+\dfrac{y^{2}}{4}-1=0.$

  Calculamos los gradientes de $f$ y $g$: \begin{eqnarray*} \nabla f\left( x,y\right) & = & \left( \dfrac{\partial f}{\partial x},\dfrac{ \partial f}{\partial y}\right) =\left( 3x^{2}y+y^{3}-y,x^{3}+3xy^{2}-x\right) \\ \nabla g\left( x,y\right) & = & \left( \dfrac{\partial g}{\partial x},\dfrac{ \partial g}{\partial y}\right) =\left( 2x,\dfrac{y}{2}\right) . \end{eqnarray*} Entonces consideramos el sistema de ecuaciones \begin{eqnarray*} \nabla f\left( x,y\right) & = & \lambda \nabla g\left( x,y\right) \\ x^{2}+\dfrac{y^{2}}{4} & = & 1, \end{eqnarray*} de donde \begin{eqnarray} 3x^{2}y+y^{3}-y & = & 2\lambda x \label{ejer5b} \\ x^{3}+3xy^{2}-x & = & \lambda \dfrac{y}{2} \notag \\ x^{2}+\dfrac{y^{2}}{4} & = & 1. \notag \end{eqnarray} Si $\lambda =0,$ entonces \begin{eqnarray*} 3x^{2}y+y^{3}-y & = & 0 \\ x^{3}+3xy^{2}-x & = & 0, \end{eqnarray*} es decir, \begin{eqnarray*} y\left( 3x^{2}+y^{2}-1\right) & = & 0 \\ x\left( x^{2}+3y^{2}-1\right) & = & 0. \end{eqnarray*} Pero este sistema lo resolvimos antes, (\ref{ejer5}), habiendo obtenido los puntos \begin{equation*} \left( 0,0\right) ,\,\left( 0,1\right) ,\,\left( -1,0\right) ,\,\left( \dfrac{1}{2},\dfrac{1}{2}\right) ,\,\left( \dfrac{1}{2},-\dfrac{1}{2}\right) ,\,\left( -\dfrac{1}{2},\dfrac{1}{2}\right) ,\,\left( -\dfrac{1}{2},-\dfrac{1 }{2}\right) ,\,\left( 1,0\right) \text{ y }\left( -1,0\right) . \end{equation*} Los siete primeros se desechan en el caso que estamos resolviendo, pues todos ellos están en el interior de la elipse, es decir, no satisfacen la restricción \begin{equation*} x^{2}+\dfrac{y^{2}}{4}=1. \end{equation*} Por lo que solamente consideramos \begin{equation*} \left( 1,0\right) \text{ y }\left( -1,0\right) \text{ con }\lambda =0. \end{equation*} Si $\lambda \neq 0,$ entonces de la primera ecuación de (\ref{ejer5b}) tenemos: \begin{equation*} 3x^{2}y+y^{3}-y=2\lambda x \end{equation*} Si $x=0,$ entonces \begin{eqnarray*} y^{3}-y & = & 0 \\ y\left( y-1\right) \left( y+1\right) & = & 0 \end{eqnarray*} de donde \begin{equation*} y=0, \quad \quad \quad y=1 \quad \quad \quad \text{ o } \quad \quad \quad y=-1 \end{equation*} Observamos que ninguno de los puntos obtenidos: $\left( 0,0\right) ,\left( 0,1\right) $ y $\left( 0,-1\right) $ satisface la restricción $g\left( x,y\right) =x^{2}+\dfrac{y^{2}}{4}-1=0$

  Si $x\neq 0,$ entonces \begin{equation*} \lambda =\dfrac{y\left( 3x^{2}+y^{2}-1\right) }{2x}. \end{equation*} sustituyendo este valor de $\lambda $ en la segunda ecuación de (\ref {ejer5b}): \begin{equation*} x^{3}+3xy^{2}-x=\dfrac{y\left( 3x^{2}+y^{2}-1\right) }{2x}\dfrac{y}{2} \end{equation*} de donde \begin{eqnarray*} 4x^{2}\left( x^{2}+3y^{2}-1\right) & = & y^{2}\left( 3x^{2}+y^{2}-1\right) \\ 4x^{4}+12x^{2}y^{2}-4x^{2} & = & 3x^{2}y^{2}+y^{4}-y^{2} \end{eqnarray*} Consideramos la restricción: $g\left( x,y\right) =x^{2}+\dfrac{y^{2}}{4} -1=0$, y despejamos $x^{2}$ \begin{equation*} x^{2}=1-\dfrac{y^{2}}{4} \end{equation*} de donde \begin{equation*} y^{2}\left( 3x^{2}+y^{2}-1\right) =4x^{2}\left( x^{2}+3y^{2}-1\right) \end{equation*} se escribe como \begin{eqnarray*} y^{2}\left( 3\left( 1-\dfrac{y^{2}}{4}\right) +y^{2}-1\right) & = & 4\left( 1- \dfrac{y^{2}}{4}\right) \left( 1-\dfrac{y^{2}}{4}+3y^{2}-1\right) \\ y^{2}\left( \dfrac{1}{4}y^{2}+2\right) & = & -\dfrac{11}{4}y^{2}\left( y^{2}-4\right) \\ y^{2}\left( \dfrac{1}{4}y^{2}+2+\dfrac{11}{4}\left( y^{2}-4\right) \right) & = & 0 \\ y^{2}\left( 3y^{2}-9\right) & = & 0 \end{eqnarray*} de donde, \begin{equation*} y=0 \quad \quad \quad y=\sqrt{3} \quad \quad \quad \text{ o } \quad \quad \quad y=-\sqrt{3} \end{equation*} Si $y=0$, entonces $\lambda =0,$ ese caso ya lo consideramos.

  Si $y=\sqrt{3}$ o $y=-\sqrt{3}$ entonces \begin{equation*} x^{2}=1-\dfrac{3}{4}=\dfrac{1}{4} \end{equation*} de donde \begin{equation*} x=\dfrac{1}{2} \quad \quad \quad \text{ o } \quad \quad \quad x=-\dfrac{1}{2} \end{equation*} Si $y=\sqrt{3},$ $x=\dfrac{1}{2},$ entonces \begin{equation*} \lambda =\dfrac{\sqrt{3}\left( 3\left( \dfrac{1}{2}\right) ^{2}+\left( \sqrt{ 3}\right) ^{2}-1\right) }{2\left( \dfrac{1}{2}\right) }=\dfrac{11}{4}\sqrt{3} \end{equation*} Si $y=\sqrt{3},$ $x=-\dfrac{1}{2},$ entonces \begin{equation*} \lambda =\dfrac{\sqrt{3}\left( 3\left( -\dfrac{1}{2}\right) ^{2}+\left( \sqrt{3}\right) ^{2}-1\right) }{2\left( -\dfrac{1}{2}\right) }=-\dfrac{11}{4} \sqrt{3} \end{equation*} Si $y=-\sqrt{3},$ $x=\dfrac{1}{2},$ entonces \begin{equation*} \lambda =\dfrac{-\sqrt{3}\left( 3\left( \dfrac{1}{2}\right) ^{2}+\left( - \sqrt{3}\right) ^{2}-1\right) }{2\left( \dfrac{1}{2}\right) }=-\dfrac{11}{4} \sqrt{3} \end{equation*} Si $y=-\sqrt{3},$ $x=-\dfrac{1}{2},$ entonces \begin{equation*} \lambda =\dfrac{-\sqrt{3}\left( 3\left( -\dfrac{1}{2}\right) ^{2}+\left( - \sqrt{3}\right) ^{2}-1\right) }{2\left( -\dfrac{1}{2}\right) }=\dfrac{11}{4} \sqrt{3} \end{equation*} Los puntos son $\left( \dfrac{1}{2},\sqrt{3}\right) $ y $\left( -\dfrac{1}{2} ,-\sqrt{3}\right) $ con $\lambda =\dfrac{11}{4}\sqrt{3},$ así como los puntos $\left( -\dfrac{1}{2},\sqrt{3}\right) $ y $\left( \dfrac{1}{2},-\sqrt{ 3}\right) $ con $\lambda =-\dfrac{11}{4}\sqrt{3}\ $satisfacen el sistema de ecuaciones (\ref{ejer5b})

  Calculamos la función \begin{eqnarray*} h\left( x,y\right) & = & f\left( x,y\right) -\lambda g\left( x,y\right) \\ & = & x^{3}y+xy^{3}-xy-\lambda \left( x^{2}+\dfrac{y^{2}}{4}-1\right) , \end{eqnarray*} \begin{eqnarray*} \dfrac{\partial h}{\partial x} & = & 3x^{2}y+y^{3}-y-2\lambda x \\ \dfrac{\partial h}{\partial y} & = & x^{3}+3xy^{2}-x-\lambda \dfrac{y}{2}. \end{eqnarray*} Las derivadas de $h$ de segundo orden son \begin{equation*} \dfrac{\partial ^{2}h}{\partial x^{2}}=6xy-2\lambda , \quad \quad \quad \dfrac{\partial ^{2}h}{\partial y^{2}}=6xy-\dfrac{\lambda }{2}, \quad \quad \quad \dfrac{\partial ^{2}h}{\partial y\partial x}=3x^{2}+3y^{2}-1. \end{equation*} Calculamos el determinante hessiano limitado \begin{eqnarray*} \left\vert \overline{H}\left( x,y\right) \right\vert & = & \left\vert \begin{array}{ccc} 0 & -\dfrac{\partial g}{\partial x}\left( x,y\right) & -\dfrac{\partial g}{ \partial y}\left( x,y\right) \\ & & \\ -\dfrac{\partial g}{\partial x}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x^{2}}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y\partial x}\left( x,y\right) \\ & & \\ -\dfrac{\partial g}{\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{ \partial x\partial y}\left( x,y\right) & \dfrac{\partial ^{2}h}{\partial y^{2}}\left( x,y\right) \\ & & \end{array} \right\vert \\ & & \\ & = & \left\vert \begin{array}{ccc} 0 & -2x & -\dfrac{y}{2} \\ & & \\ -2x & 6xy-2\lambda & 3x^{2}+3y^{2}-1 \\ & & \\ -\dfrac{y}{2} & 3x^{2}+3y^{2}-1 & 6xy-\dfrac{\lambda }{2} \end{array} \right\vert \\ & & \\ & = & -4x^{2}\left( 6xy-\dfrac{\lambda }{2}\right) +2xy\left( 3x^{2}+3y^{2}-1\right) -\dfrac{y^{2}}{2}\left( 3xy-\lambda \right) , \end{eqnarray*} de donde, \begin{equation*} \left\vert \overline{H}\left( x,y\right) \right\vert =-4x^{2}\left( 6xy- \dfrac{\lambda }{2}\right) +2xy\left( 3x^{2}+3y^{2}-1\right) -\dfrac{y^{2}}{2 }\left( 3xy-\lambda \right) . \end{equation*} Ahora evaluamos en los siguientes puntos:

  Para los puntos $\left( -1,0\right) $, $\left( 1,0\right) $ y $\lambda =0.$ \begin{equation*} \left\vert \overline{H}\left( \pm 1,0\right) \right\vert =0, \end{equation*} el criterio no da información.

  Para saber qué sucede en el punto $\left( 1,0\right) ,$ observamos que, evaluando $f\left( x,y\right) =xy\left( x^{2}+y^{2}-1\right) $ en $\left( 1,0\right) $ tenemos \begin{equation*} f\left( 1,0\right) =0. \end{equation*} Consideremos un punto sobre la elipse con coordenadas \begin{equation*} \left( \sqrt{1-\dfrac{y^{2}}{4}},y\right) , \end{equation*} Cuando $y$ es peque\~{n}a positiva, el punto se aproxima al punto de coordenadas $\left( 1,0\right) $ y \begin{equation*} f\left( x,y\right) =xy\left( x^{2}+y^{2}-1\right) >0, \end{equation*} ya que \begin{eqnarray*} x^{2}+y^{2}-1 & = & \left( \sqrt{1-\dfrac{y^{2}}{4}}\right) ^{2}+y^{2}-1 \\ & = & 1-\dfrac{y^{2}}{4}+y^{2}-1=\dfrac{3}{4}y^{2}>0 \end{eqnarray*} y tanto $x$ como $y$ son positivos, por lo que $xy$ es también positivo.

  Por otra parte,considerando $y$ negativa con $\left\vert y\right\vert $ peque \~{n}o, la expresión $x^{2}+y^{2}-1$ es positiva como en el otro caso, pero ahora $x$ es positivo y $y$ es negativo, por lo que $xy<0,$ de donde \begin{equation*} f\left( x,y\right) =xy\left( x^{2}+y^{2}-1\right) < 0, \end{equation*}

  entonces concluimos que $\left( 1,0\right) $ es un punto silla.

  Para el punto de coordenadas $\left( -1,0\right) ,$ podemos hacer un aná lisis similar, en ese caso: \begin{equation*} f\left( -1,0\right) =0 \end{equation*} y un punto sobre la elipse, con abscisa negativa, tiene coordenadas \begin{equation*} \left( -\sqrt{1-\dfrac{y^{2}}{4}},y\right) . \end{equation*} Analizando el signo de la función $f$ en los puntos anteriores, considerando $\left\vert y\right\vert $ peque\~{n}o, en un caso positiva y en otro negativa, tenemos que $f$ tiene un punto silla en $\left( -1,0\right) .$

  Para los puntos $\left( -\dfrac{1}{2},-\sqrt{3}\right) ,$ $\left( \dfrac{1}{2 },\sqrt{3}\right) $ con $\lambda =\dfrac{11}{4}\sqrt{3}$ el hessiano vale

  $ \begin{array}{l} -4\left( \dfrac{1}{4}\right) \left( 6\left( \dfrac{1}{2}\right) \sqrt{3}- \dfrac{1}{2}\dfrac{11\sqrt{3}}{4}\right) +2\left( \dfrac{1}{2}\right) \sqrt{3 }\left( \dfrac{3}{4}+3\left( 3\right) -1\right) -\dfrac{3}{2}\left( 3\left( \dfrac{1}{2}\right) \sqrt{3}-\dfrac{11\sqrt{3}}{4}\right) \\ \\ =-\dfrac{13}{8}\sqrt{3}+\dfrac{35}{4}\sqrt{3}+\dfrac{15}{8}\sqrt{3} \\ \\ =9\sqrt{3}>0, \end{array} $

  entonces en estos puntos hay un máximo relativo.

  Para los puntos $\left( -\dfrac{1}{2},\sqrt{3}\right) ,$ $\left( \dfrac{1}{2} ,-\sqrt{3}\right) $ con $\lambda =-\dfrac{11}{4}\sqrt{3}$ el hessiano vale

  \[ \begin{array}{l} -4\left( \dfrac{1}{4}\right) \left( 6\left( -\dfrac{1}{2}\right) \sqrt{3}+ \dfrac{1}{2}\dfrac{11\sqrt{3}}{4}\right) +2\left( -\dfrac{1}{2}\right) \sqrt{ 3}\left( \dfrac{3}{4}+3\left( 3\right) -1\right) -\dfrac{3}{2}\left( 3\left( -\dfrac{1}{2}\right) \sqrt{3}+\dfrac{11\sqrt{3}}{4}\right) \\ \\ =\dfrac{13}{8}\sqrt{3}-\dfrac{35}{4}\sqrt{3}-\dfrac{15}{8}\sqrt{3} \\ \\ =-9\sqrt{3} < 0, \end{array} \]

  entonces en estos puntos hay un mínimo relativo.