Máximos y Mínimos de Funciones de Varias Variables

Solución:

La función es polinomial, por lo que las derivadas parciales existen en todo el plano, entonces los valores extremos se pueden alcanzar en:

• el interior de la región, en los puntos estacionarios, o bien,
• los puntos frontera de la región.

• Puntos estacionarios:

  Calculamos las derivadas parciales de primer orden de la función $f\left( x,y\right) =x^{3}+y^{3}+3x^{2}-3y^{2}+5.$ \begin{equation*} \dfrac{\partial f}{\partial x}\left( x,y\right) =3x^{2}+6x=3x\left( x+2\right) \quad \quad \quad \text{y} \quad \quad \quad \frac{\partial f}{ \partial y}\left( x,y\right) =3y^{2}-6y=3y\left( y-2\right) \end{equation*} Igualamos a cero las derivadas de primer orden para determinar los puntos estacionarios \begin{eqnarray*} 3x\left( x+2\right) & = & 0 \\ 3y\left( y-2\right) & = & 0, \end{eqnarray*} de donde \begin{equation*} x=0, \quad \quad x=-2, \quad \quad y=0, \quad \quad y=2 \end{equation*} Los puntos estacionarios son \begin{equation*} A\left( 0,0\right) , \quad \quad B\left( 0,2\right) , \quad \quad C\left( -2,0\right) , \quad \quad D\left( -2,2\right) \end{equation*} Observamos que todos los puntos se encuentran en el interior de la región.

  

  Calculamos las derivadas de segundo orden. \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( x,y\right) =6x+6, \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y^{2}}\left( x,y\right) =6y-6, \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y\partial x}\left( x,y\right) =0= \dfrac{\partial ^{2}f}{\partial x\partial y}\left( x,y\right) \end{equation*} Analizamos $\dfrac{\partial ^{2}f}{\partial x^{2}}$ y el determinante hessiano en los puntos estacionarios.

  • En $A\left( 0,0\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,0\right) & = & 6\left( 0\right) +6=6 \\ \dfrac{\partial ^{2}f}{\partial y^{2}}\left( 0,0\right) & = & 6\left( 0\right) -6=-6 \\ \dfrac{\partial ^{2}f}{\partial y\partial x}\left( 0,0\right) & = & 0, \end{eqnarray*} de donde \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,0\right) & = & 6>0 \\ \left\vert H\left( 0,0\right) \right\vert & = & 6\left( -6\right) < 0. \end{eqnarray*}

    entonces en $A\left( 0,0\right) $ hay un punto silla.

  • En $B\left( 0,2\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,2\right) & = & 6\left( 0\right) +6=6 \\ \dfrac{\partial ^{2}f}{\partial y^{2}}\left( 0,2\right) & = & 6\left( 2\right) -6=6 \\ \dfrac{\partial ^{2}f}{\partial y\partial x}\left( 0,2\right) & = & 0, \end{eqnarray*} de donde \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( 0,2\right) & = & 6>0 \\ \left\vert H\left( 0,2\right) \right\vert & = & 6\left( 6\right) >0 \end{eqnarray*} entonces en $B\left( 0,2\right) $ hay un mínimo relativo y el valor de la función en ese punto es \begin{equation*} f\left( 0,2\right) =1. \end{equation*}
  • En $C\left( -2,0\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -2,0\right) & = & 6\left( -2\right) +6=-6 \\ \dfrac{\partial ^{2}f}{\partial y^{2}}\left( -2,0\right) & = & 6\left( 0\right) -6=-6, \\ \dfrac{\partial ^{2}f}{\partial y\partial x}\left( -2,0\right) & = & 0 \end{eqnarray*} de donde \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -2,0\right) & = & -6 < 0 \\ \left\vert H\left( -2,0\right) \right\vert & = & -6\left( -6\right) > 0 \end{eqnarray*} entonces en $C\left( -2,0\right) $ hay un máximo relativo y el valor de la función en ese punto es \begin{equation*} f\left( -2,0\right) =9. \end{equation*}
  • En $D\left( -2,2\right) $ \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -2,2\right) & = & 6\left( -2\right) +6=-6 \\ \dfrac{\partial ^{2}f}{\partial y^{2}}\left( -2,2\right) & = & 6\left( 2\right) -6=6 \\ \dfrac{\partial ^{2}f}{\partial y\partial x}\left( -2,2\right) & = & 0, \end{eqnarray*} de donde \begin{eqnarray*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( -2,2\right) & = & -6 < 0 \\ \left\vert H\left( -2,2\right) \right\vert & = & -6\left( 6\right) < 0 \end{eqnarray*}

    entonces en $D\left( -2,2\right) $ hay un punto silla.

• Los puntos frontera son los de los lados del cuadrado.

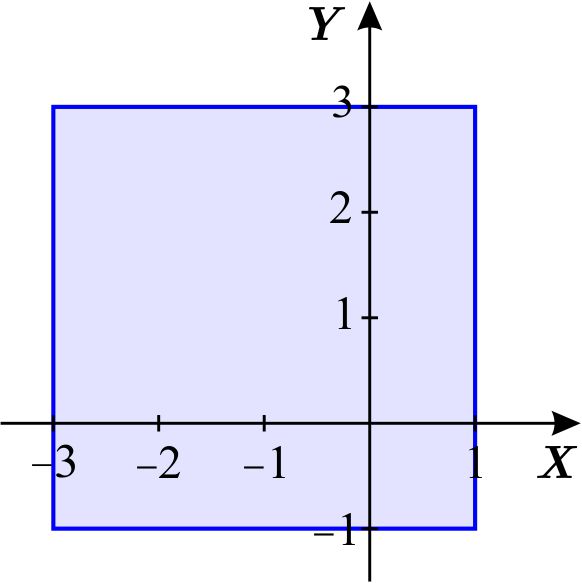
  Las ecuaciones de los lados del cuadrado son \begin{equation*} \left\{ \begin{array}{lcc} y=-1 & & \text{con }-3\leq x\leq 1 \\ y=3 & & \text{con }-3\leq x\leq 1 \\ x=-3 & & \text{con }-1\leq y\leq 3 \\ x=1 & & \text{con }-1\leq y\leq 3. \end{array} \right. \end{equation*} Restringimos la función $f\left( x,y\right) =x^{3}+y^{3}+3x^{2}-3y^{2}+5$ a cada lado del cuadrado.

  • Si $y=-1,$ entonces \begin{equation*} f\left( x,-1\right) =x^{3}+3x^{2}+1 \end{equation*} con $-3\leq x\leq 1.$ Los puntos extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -3,1\right] $: $-3$ y $1$. Que corresponden a $E\left( -3,-1\right)$ y $F\left( 1,-1\right)$. Ahí los valores de $f\left( x,-1\right) $ son \begin{eqnarray*} f\left( -3,-1\right) & = & 1 \\ f\left( 1,-1\right) & = & 5; \end{eqnarray*}

    (ii) Los puntos interiores de $\left[ -3,1\right] $ donde la derivada de $ f\left( x,-1\right) $ se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dx}\left( x,-1\right) =3x^{2}+6x=3x\left( x+2\right) \end{equation*} y la igualamos a cero, para encontrar el valor de $x$ \begin{equation*} 3x\left( x+2\right) =0 \end{equation*} si \begin{equation*} x=0 \quad \quad \quad \text{o} \quad \quad \quad x=-2. \end{equation*} Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( x,-1\right) =6x+6 \end{equation*} y evaluamos en los puntos $x=0$ y $x=-2$, que corresponden a $G\left( 0,-1\right)$ y $H\left( -2,-1\right)$

    Si $x=0,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( 0,-1\right) =6>0 \end{equation*} así $f\left( x,-1\right) $ alcanza un mínimo relativo en $0.$ El valor de la función es \begin{equation*} f\left( 0,-1\right) =1. \end{equation*}

    Si $x=-2,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( -2,-1\right) =-6 < 0 \end{equation*}

    así $f\left( x,-1\right) $ alcanza un máximo relativo en $-2.$ El valor de la función es \begin{equation*} f\left( -2,-1\right) =5. \end{equation*}

  • Si $y=3,$ entonces \begin{equation*} f\left( x,3\right) =x^{3}+3x^{2}+5 \end{equation*} con $-3\leq x\leq 1.$ Los puntos extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -3,1\right] $: $-3$ y $1$, que corresponden a $I\left( -3,3\right)$ y $J\left( 1,3\right)$, Ahí los valores de $f\left( x,3\right) $ son \begin{eqnarray*} f\left( -3,3\right) & = & 5 \\ f\left( 1,3\right) & = & 9; \end{eqnarray*}

    (ii) En los puntos interiores de $\left[ -3,1\right] $ donde la derivada de $ f\left( x,3\right) $ se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dx}\left( x,3\right) =3x^{2}+6x=3x\left( x+2\right) \end{equation*} así \begin{equation*} 3x\left( x+2\right) =0 \end{equation*} si \begin{equation*} x=0 \quad \quad \quad \text{o} \quad \quad \quad x=-2. \end{equation*} Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( x,3\right) =6x+6 \end{equation*} y evaluamos en los puntos $x=0$ y $x=-2$, que corresponden a $K\left( 0,3\right)$ y $L\left( -2,3\right)$

    Si $x=0,$ entonces \begin{equation*} \dfrac{d^{2}f}{dx^{2}}\left( 0,3\right) =6>0 \end{equation*} así $f\left( x,3\right) $ alcanza un mínimo relativo en $K\left(0,3\right) .$ El valor de la función es \begin{equation*} f\left( 0,3\right) =5. \end{equation*} Si $x=-2,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( -2,3\right) =-6 < 0 \end{equation*}

    así $f\left( x,3\right) $ alcanza un máximo relativo en $L\left(-2,3\right)$. El valor de la función es \begin{equation*} f\left( -2,3\right) =9. \end{equation*}

  • Si $x=-3,$ entonces \begin{equation*} f\left( -3,y\right) =y^{3}-3y^{2}+5 \end{equation*} con $-1\leq y\leq 3$. Los puntos extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -1,3\right] $: $-1$ y $3$, que corresponden a los puntos $E\left( -3,-1\right)$ y $I\left( -3,3\right)$ que ya teníamos. Ahí los valores de $f\left( -3,y\right) $ son \begin{eqnarray*} f\left( -3,-1\right) & = & 1 \\ f\left( -3,3\right) & = & 5; \end{eqnarray*}

    (ii) En los puntos interiores de $\left[ -1,3\right] $ donde la derivada de $ f\left( -3,y\right) $ \begin{equation*} \dfrac{df}{dy}\left( -3,y\right) =3y^{2}-6y=3y\left( y-2\right) \end{equation*} se anula.

    Tenemos \begin{equation*} 3y\left( y-2\right) =0 \end{equation*} si \begin{equation*} y=0 \quad \quad \quad \text{o} \quad \quad \quad y=2. \end{equation*} Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( -3,y\right) =6y-6 \end{equation*} y evaluamos en los puntos $y=0$ y $y=2$ que corresponden a $M\left( -3,0\right)$ y $N\left( -3,2\right)$

    Si $y=0,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( -3,0\right) =-6 < 0 \end{equation*}

    así $f\left( -3,y\right) $ alcanza un máximo relativo en $M\left(-3,0\right) .$ El valor de la función es \begin{equation*} f\left( -3,0\right) =5 \end{equation*} Si $y=2,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( -3,2\right) =6>0 \end{equation*} así, $f\left( -3,y\right) $ alcanza un mínimo relativo en $N\left( -3,2\right)$. El valor de la función es \begin{equation*} f\left( -3,2\right) =1. \end{equation*}

  • Si $x=1,$ entonces \begin{equation*} f\left( 1,y\right) =y^{3}-3y^{2}+9 \end{equation*} con $-1\leq y\leq 3$. Los puntos extremos se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ -1,3\right] $: $-1$ y $3$, que corresponden a $F\left( 1,-1\right)$ y $J\left( 1,3\right)$ que ya teníamos. Ahí los valores de $f\left( 1,y\right) $ son \begin{eqnarray*} f\left( 1,-1\right) & = & 5 \\ f\left( 1,3\right) & = & 9; \end{eqnarray*}

    (ii) Los puntos interiores de $\left[ -1,3\right] $ donde la derivada de $ f\left( 1,y\right) $: \begin{equation*} \dfrac{df}{dy}\left( 1,y\right) =3y^{2}-6y=3y\left( y-2\right) \end{equation*} se anula.

    Tenemos \begin{equation*} 3y\left( y-2\right) =0 \end{equation*} si \begin{equation*} y=0 \quad \quad \quad \text{o} \quad \quad \quad y=2. \end{equation*} Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( 1,y\right) =6y-6 \end{equation*} y evaluamos en los puntos $y=0$ y $y=2.$

    Si $y=0,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( 1,0\right) =-6 < 0 \end{equation*}

    así $f\left( 1,y\right) $ alcanza un máximo relativo en $O\left( 1,0\right).$ El valor de la función es \begin{equation*} f\left( 1,0\right) =9. \end{equation*} Si $y=2,$ entonces \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( 1,2\right) =6>0 \end{equation*} así $f\left( 1,y\right) $ alcanza un mínimo relativo en $P\left( 1,2\right).$ El valor de la función es \begin{equation*} f\left( 1,2\right) =5. \end{equation*}

  Los valores de la función obtenidos en los puntos que son candidatos a ser máximo o mínimo absolutos son: \begin{equation*} \begin{array}{lllll} f\left( 0,2\right) =1 & f\left( -3,-1\right) =1 & f\left( -3,3\right) =5 & f\left( -3,3\right) =5 & f\left( 1,-1\right) =5 \\ f\left( -2,0\right) =9 & f\left( 1,-1\right) =5 & f\left( 1,3\right) =9 & f\left( -3,0\right) =5 & f\left( -2,-1\right) =5 \\ f\left( 1,0\right) =9 & f\left( 0,-1\right) =1 & f\left( 0,3\right) =5 & f\left( -3,2\right) =1 & f\left( -2,3\right) =9 \\ f\left( 1,2\right) =5. & & & & \end{array} \end{equation*}