Máximos y Mínimos de Funciones de Varias Variables Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Ejemplo 1

Solución:

Como la función es polinomial, las derivadas parciales existen en todo el plano, entonces los valores extremos se pueden alcanzar en

• el interior de la región, en los puntos estacionarios o bien,
• en los puntos frontera de la región.

• Puntos estacionarios:

  Calculamos las derivadas parciales de primer orden de la función $f\left( x,y\right) =x^{2}+y^{2}-8x-4y+1$ \begin{equation*} \dfrac{\partial f}{\partial x}\left( x,y\right) =2x-8 \quad \quad \quad \text{ y } \quad \quad \quad \frac{\partial f}{\partial y}\left( x,y\right) =2y-4. \end{equation*} Igualamos a cero las derivadas de primer orden para determinar los puntos estacionarios \begin{eqnarray*} 2x-8 & = & 0 \\ 2y-4 & = & 0, \end{eqnarray*} de donde \begin{equation*} x=4 \quad \quad \quad \text{ y } \quad \quad \quad y=2. \end{equation*} Observamos que el punto $A\left( 4,2\right) $ se encuentra en el interior de la región.

  Calculamos las derivadas de segundo orden. \begin{equation*} \dfrac{\partial ^{2}f}{\partial x^{2}}\left( x,y\right) =2, \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y^{2}}\left( x,y\right) =2, \quad \quad \quad \dfrac{\partial ^{2}f}{\partial y\partial x}\left( x,y\right) =0=\dfrac{ \partial ^{2}f}{\partial x\partial y}\left( x,y\right) , \end{equation*} de donde, el determinante hessiano es \begin{equation*} \left\vert H\left( x,y\right) \right\vert =\left\vert \begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right\vert =4. \end{equation*} Como

  • $\dfrac{\partial ^{2}f}{\partial x^{2}}\left( 4,2\right) =2>0$ y
  • $\left\vert H\left( 4,2\right) \right\vert =4>0,$

  entonces en $A\left( 4,2\right) $ se alcanza un mínimo relativo y este valor es \begin{equation*} f(4,2)=-19. \end{equation*}

  

• Los puntos frontera son los que están en los lados del triángulo.

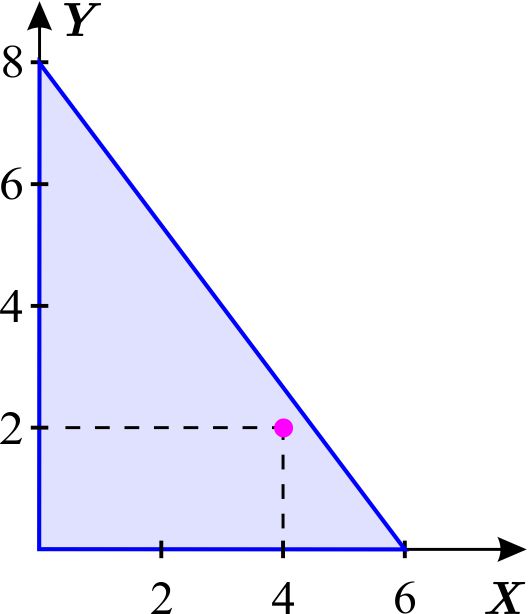
  Las ecuaciones de los lados del triángulo son \begin{equation*} \left\{ \begin{array}{lcc} y=0 & & \text{con } 0\leq x\leq 6 \\ x=0 & & \text{con } 0\leq y\leq 8 \\ y=-\dfrac{4}{3}x+8 & & \text{con }0\leq x\leq 6. \end{array} \right. \end{equation*}

  • Si $y=0,$ entonces \begin{equation*} f\left( x,0\right) =x^{2}-8x+1 \end{equation*} con $0\leq x\leq 6.$ Los valores extremos de $f\left( x,0\right) $ en $\left[ 0,6\right] $ se pueden alcanzar en:

    (i) los extremos del intervalo $\left[ 0,6\right] $: $0$ y $6$, que corresponden a $B\left( 0,0\right)$ y $C\left( 6,0\right)$. Ahí los valores de $f$ son \begin{eqnarray*} f\left( 0,0\right) & = & 1 \\ f\left( 6,0\right) & = & -11; \end{eqnarray*}

    (ii) En los puntos interiores del intervalo $\left[ 0,6\right] $ donde la derivada se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dx}\left( x,0\right) =2x-8 \end{equation*} y la igualamos a cero, para encontrar el valor de $x$ \begin{equation*} 2x-8=0, \end{equation*} es decir, $x=4.$

    Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dx^{2}}\left( x,0\right) =2>0 \end{equation*} entonces $D\left( 4,0\right) $ es un mínimo relativo de $f(x,0)$ y \begin{equation*} f\left( 4,0\right) =-15. \end{equation*}

  • Si $x=0,$ entonces \begin{equation*} f\left( 0,y\right) =y^{2}-4y+1 \end{equation*} con $0\leq y\leq 8.$ Los valores extremos de $f\left( 0,y\right) $ en $\left[ 0,8\right] $se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ 0,8\right] $: $0$ y $8$, que corresponden a $B\left( 0,0\right)$ que ya teníamos y a $E\left( 0,8\right)$. Ahí los valores de $f$ son \begin{eqnarray*} f\left( 0,0\right) & = & 1 \\ f\left( 0,8\right) & = & 33; \end{eqnarray*}

    (ii) En los puntos interiores donde la derivada se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dy}\left( 0,y\right) =2y-4 \end{equation*} y la igualamos a cero, para encontrar el valor de $y$ \begin{equation*} 2y-4=0, \end{equation*} es decir, $y=2.$

    Calculamos la segunda derivada \begin{equation*} \dfrac{d^{\,2}f}{dy^{2}}\left( 0,y\right) =2>0, \end{equation*} entonces $F\left( 0,2\right) $ es un mínimo relativo de $f(0,y)$ en $ \left[ 0,8\right] $ y \begin{equation*} f\left( 0,2\right) =4-8+1=-3. \end{equation*}

  • Si $y=-\dfrac{4}{3}x+8,$ entonces \begin{equation*} f\left( x,-\dfrac{4}{3}x+8\right) =\dfrac{25}{9}x^{2}-24x+33 \end{equation*} con $0\leq x\leq 6.$ Los valores extremos de $f\left( x,-\dfrac{4}{3} x+8\right) $ en $\left[ 0,6\right] $ se pueden alcanzar en:

    (i) Los extremos del intervalo $\left[ 0,6\right] $: $0$ y $6$, que corresponden a los puntos $E\left( 0,8\right)$ y $C\left( 6,0\right)$ que ya teníamos. Ahí los valores de $f$ son \begin{eqnarray*} f\left( 0,8\right) & = & 33 \\ f\left( 6,0\right) & = & -11; \end{eqnarray*}

    (ii) En los puntos interiores del intervalo $\left[ 0,6\right] $ donde la derivada se anula.

    Calculamos la derivada, \begin{equation*} \dfrac{df}{dx}\left( x,-\dfrac{4}{3}x+8\right) =\dfrac{50}{9}x-24 \end{equation*} y la igualamos a cero, para encontrar el valor de $x$ \begin{eqnarray*} \dfrac{50}{9}x-24 & = & 0 \\ x & = & \dfrac{108}{25}=4.32. \end{eqnarray*} Para este valor de $x=\dfrac{108}{25},$ el valor de $y$ es \begin{equation*} y=\dfrac{56}{25}=2.24 \end{equation*} Observación: El punto $G\left( \dfrac{108}{25},\dfrac{56}{25}\right) $ está en la hipotenusa del triángulo y puede verificarse que es el punto de la hipotenusa más cercano al punto estacionario $A\left( 4,2\right) $ previamente analizado.

    Calculamos la segunda derivada \begin{equation*} \dfrac{d\,^{2}f}{dx^{2}}\left( x,-\dfrac{4}{3}x+8\right) =\dfrac{50}{9}>0 \end{equation*} entonces en $G\left( \dfrac{108}{25},\dfrac{56}{25}\right) $ hay un mínimo relativo de $f\left( x,-\dfrac{4}{3}x+8\right) $ en $\left[ 0,6\right] $ , cuyo valor es \begin{equation*} f\left( \dfrac{108}{25},\dfrac{56}{25}\right) =-\dfrac{471}{25}=-18.84. \end{equation*}