Integrales Triples Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Cambio de Variables

Sean \(W_{1}\subset \mathbb{R}^{3} \) una región elemental y \( T:W_{1}\rightarrow \mathbb{R}^{3} \) una transformación inyectiva y de clase \(C^{1} \) excepto quizás en la frontera de \(W_{1}. \) Si \(T\left( W_{1}\right) =W \) es una región elemental y \(f:W\rightarrow \mathbb{R}, \) es una función integrable entonces \begin{eqnarray*} \iiint_{W}f\left( x,y,z\right) \,dx\,dy\,dz &=&\iiint_{W_{1}}\left( f\circ T\right) \left( u,v,w\right) \left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( u,v,w\right) }\right\vert \,du\,dv\,dw \\ &=&\iiint_{W_{1}}f\left( x\left( u,v,w\right) ,y\left( u,v,w\right) ,z\left( u,v,w\right) \right) \left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( u,v,w\right) }\right\vert \,du\,dv\,dw, \end{eqnarray*} donde \(T\left( u,v,w\right) =\left( x\left( u,v,w\right) ,y\left( u,v,w\right) ,z\left( u,v,w\right) \right) \) y \(\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( u,v,w\right) }\right\vert \) es el valor absoluto del jacobiano de \(T. \)

Jacobiano de la transformación cilíndrica

Jacobiano de la transformación esférica

Su regla de correspondencia es \begin{equation*} T_{e}\left( \rho ,\theta ,\phi \right) =\left( \rho \cos \theta\ \text{sen}\ \phi , \rho\ \text{sen}\ \theta\ \text{sen}\ \phi ,\rho \cos \phi \right) . \end{equation*} El jacobiano de la transformación esférica \(T_{e} \) es : \begin{eqnarray*} \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) } &=&\det \left( \begin{array}{ccc} \cos \theta\ \text{sen}\ \phi & -\rho\ \text{sen}\ \theta\ \text{sen}\ \phi & \rho \cos \theta \cos \phi \\ \text{sen}\ \theta\ \text{sen}\ \phi & \rho \cos \theta\ \text{sen}\ \phi & \rho\ \text{sen}\ \theta \cos \phi \\ \cos \phi & 0 & -\rho\ \text{sen}\ \phi \end{array} \right) \\ &=&\cos \phi \det \left( \begin{array}{cc} -\rho\ \text{sen}\ \theta\ \text{sen}\ \phi & \rho \cos \theta \cos \phi \\ \rho \cos \theta\ \text{sen}\ \phi & \rho\ \text{sen}\ \theta \cos \phi \end{array} \right) -\rho\ \text{sen}\ \phi \det \left( \begin{array}{cc} \cos \theta\ \text{sen}\ \phi & -\rho\ \text{sen}\ \theta\ \text{sen}\ \phi \\ \text{sen}\ \theta\ \text{sen}\ \phi & \rho \cos \theta\ \text{sen}\ \phi \end{array} \right) \\ &=&\cos \phi \left( -\rho ^{2} \text{sen}\ \phi \cos \phi \text{sen} ^{2}\theta -\rho ^{2} \text{sen}\ \phi \cos \phi \cos ^{2}\theta \right) -\rho\ \text{sen}\ \phi \left( \rho\ \text{sen} ^{2}\phi \cos ^{2}\theta +\rho\ \text{sen} ^{2}\phi\ \text{sen} ^{2}\theta \right) \\ &=&\cos \phi \left( -\rho ^{2} \text{sen}\ \phi \cos \phi \right) \left( \text{sen} ^{2}\theta +\cos ^{2}\theta \right) -\rho\ \text{sen}\ \phi \left( \rho\ \text{sen} ^{2}\phi \right) \left( \cos ^{2}\theta + \text{sen} ^{2}\theta \right) \\ &=&-\rho ^{2} \text{sen}\ \phi \cos ^{2}\phi -\rho ^{2} \text{sen} ^{3}\phi \\ &=&-\rho ^{2} \text{sen}\ \phi \left( \cos ^{2}\phi + \text{sen} ^{2}\phi \right) \\ &=&-\rho ^{2} \text{sen}\ \phi . \end{eqnarray*}

Ejemplos

1. Calcular el volumen de la esfera \(W \) con centro en el origen y radio \( a. \)

    

   Solución:

    

    

    

    

   

    

    

    

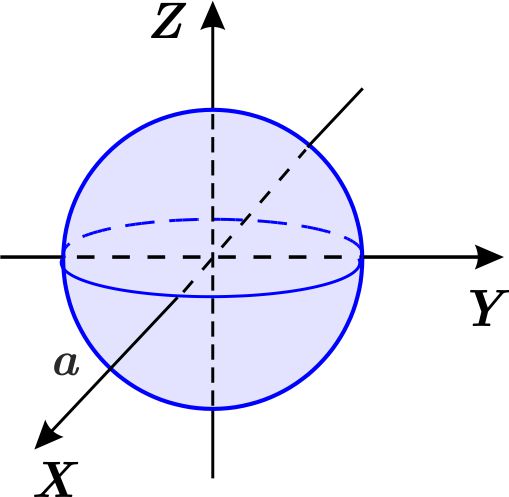
   Resolveremos el problema usando coordenadas cartesianas, cilíndricas y esféricas. En el caso de coordenadas cartesianas, solamente escribiremos la integral que debería calcularse.

   • Coordenadas cartesianas.

     La ecuación de la esfera es \begin{equation*} x^{2}+y^{2}+z^{2}\ \leq a^{2}. \end{equation*} Presentaremos a \(W \) como una región del tipo \(I. \) La proyección de la esfera sobre el plano \(XY \) es el disco con centro en el origen y radio \(a \) : \begin{equation*} x^{2}+y^{2}\leq a^{2}. \end{equation*} Así, podemos considerar el conjunto \(D \) de tipo 1 en el plano \(XY \) como \begin{equation*} D=\left\{ \left( x,y\right) \left\vert \,-a\leq x\leq a,\quad -\sqrt{a-x^{2}} \leq y\leq \sqrt{a-x^{2}}\right. \right\} . \end{equation*} Ahora despejamos \(z \) en la ecuación de la esfera \begin{eqnarray*} x^{2}+y^{2}+z^{2} &=&a^{2} \\ z^{2} &=&a^{2}-\left( x^{2}+y^{2}\right) \\ \left\vert z\right\vert &=&\sqrt{a^{2}-\left( x^{2}+y^{2}\right) }, \end{eqnarray*} de donde \begin{equation*} z=-\sqrt{a^{2}-\left( x^{2}+y^{2}\right) }\quad \quad \quad \text{ o }\quad \quad \quad z=\sqrt{a^{2}-\left( x^{2}+y^{2}\right) }. \end{equation*} Así, la esfera \(W \) con centro en el origen y radio \(a, \) como región de tipo I se puede escribir como: \begin{equation*} W=\left\{ \left( x,y,z\right) \left\vert \,\left( x,y\right) \in D,\quad - \sqrt{a^{2}-\left( x^{2}+y^{2}\right) }\leq z\leq \sqrt{a^{2}-\left( x^{2}+y^{2}\right) }\right. \right\} . \end{equation*} Entonces el volumen de la esfera es: \begin{equation*} \text{Vol }W=\int_{-a}^{a}\int_{-\sqrt{a^{2}-x^{2}}}^{ \sqrt{a^{2}-x^{2}}}\int_{-\sqrt{a^{2}-\left( x^{2}+y^{2}\right) } }^{\sqrt{a^{2}-\left( x^{2}+y^{2}\right) }}dz\,dy\,dx. \end{equation*} La región plana \(D \) está descrita como de tipo 1, pero también es de tipo 2. Por tanto, podemos cambiar el orden de integración a \( dz\,dx\,dy \)

   • Coordenadas cilíndricas.

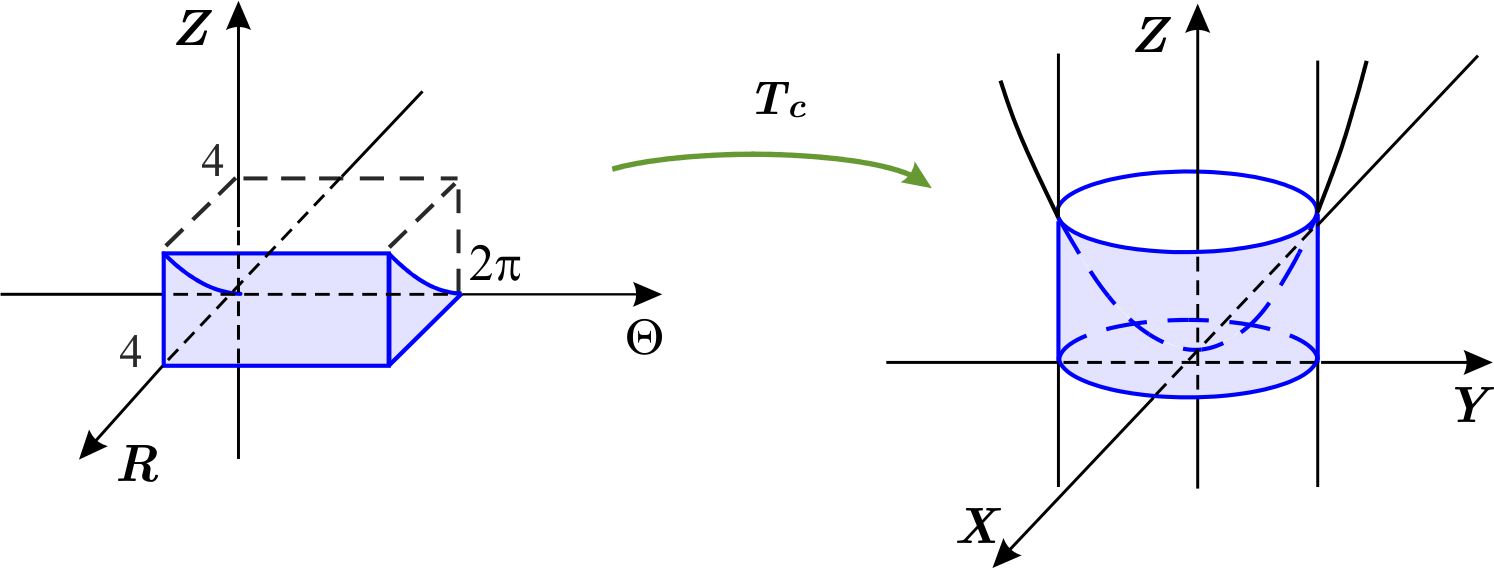
     Escribimos la ecuación de la esfera en coordenadas cilíndricas \begin{eqnarray*} x^{2}+y^{2}+z^{2} &=&a^{2} \\ r^{2}\cos ^{2}\theta +r^{2} \text{sen} ^{2}\theta +z^{2} &=&a^{2} \\ r^{2}+z^{2} &=&a^{2} \\ z^{2} &=&a^{2}-r^{2} \\ \left\vert z\right\vert &=&\sqrt{a^{2}-r^{2}}, \end{eqnarray*} de donde, \begin{equation*} z=-\sqrt{a^{2}-r^{2}}\quad \quad \quad \text{o}\quad \quad \quad z=\sqrt{ a^{2}-r^{2}}. \end{equation*} La proyección de la esfera sobre el plano \(XY \) es el círculo \begin{eqnarray*} x^{2}+y^{2} &\leq &a^{2} \\ r^{2} &\leq &a^{2} \\ r &\leq &a. \end{eqnarray*} Entonces \begin{equation*} W_{1}=\left\{ \left( r,\theta ,z\right) \left\vert \,0\leq \theta \leq 2\pi ,\quad 0\leq r\leq a,\quad -\sqrt{a^{2}-r^{2}}\leq z\leq \sqrt{a^{2}-r^{2}} \right. \right\} \end{equation*} que es una región del tipo I en el sistema \(R\Theta Z \) y es el conjunto de coordenadas cilíndricas de los puntos de la región \(W \) . Por tanto, su imagen bajo la transformación cilíndrica \(T_{c} \) es \(W \) .

      

      

      

     

      

      

      

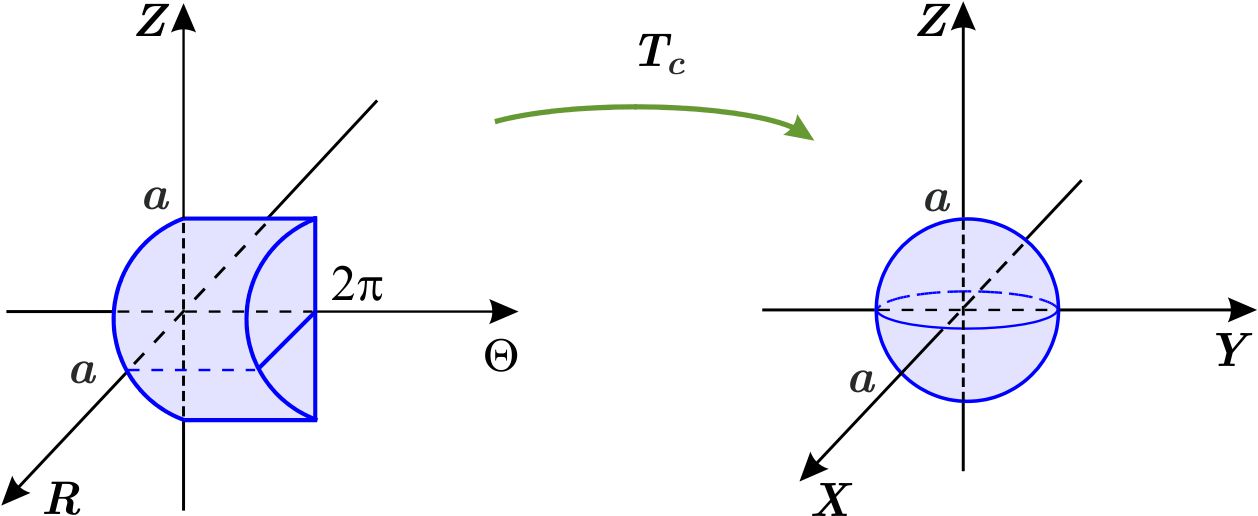
     Sabemos que el jacobiano de la transformación cilíndrica es \(\dfrac{ \partial \left( x,y,z\right) }{\partial \left( r,\theta ,z\right) }=r. \)

     Aplicamos el Teorema de cambio de variables. \begin{eqnarray*} \text{Vol }W &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( r,\theta ,z\right) }\right\vert dr\,d\theta \,dz\text{ } \\ \int_{0}^{2\pi }\int_{0}^{a}\int_{-\sqrt{ a^{2}-r^{2}}}^{\sqrt{a^{2}-r^{2}}}rdz\,dr\,d\theta &=&\int_{0}^{2\pi }\int_{0}^{a}\left. rz\right\vert _{- \sqrt{a^{2}-r^{2}}}^{\sqrt{a^{2}-r^{2}}}dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{a}r\left( \sqrt{a^{2}-r^{2}} +\sqrt{a^{2}-r^{2}}\right) \,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{a}2r\sqrt{a^{2}-r^{2}} dr\,d\theta \\ &=&\int_{0}^{2\pi }\left. \dfrac{-\left( a^{2}-r^{2}\right) ^{ \frac{3}{2}}}{\frac{3}{2}}\right\vert _{0}^{a}\,d\theta \\ &=&\int_{0}^{2\pi }\dfrac{2}{3}a^{3}d\theta \\ &=&\dfrac{2}{3}a^{3}\left( 2\pi \right) \\ &=&\dfrac{4}{3}\pi a^{3}. \end{eqnarray*}

   • Coordenadas esféricas.

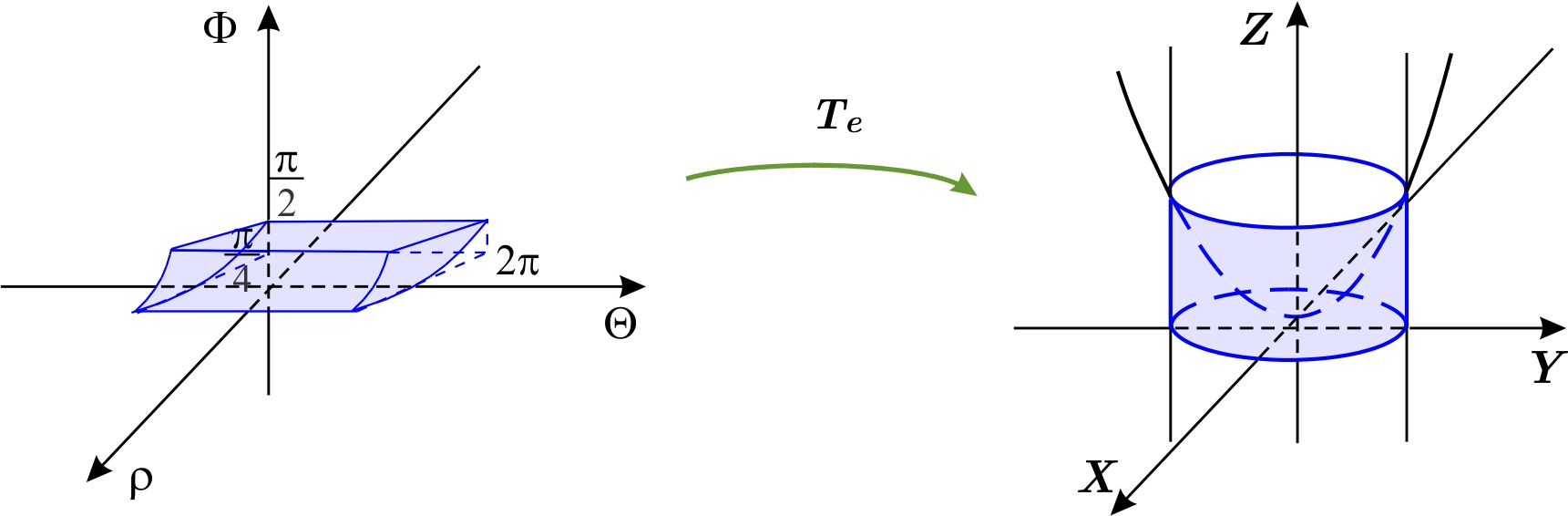
     Escribimos la ecuación de la esfera en coordenadas esféricas \begin{eqnarray*} x^{2}+y^{2}+z^{2} &=&a^{2} \\ \rho ^{2}\cos ^{2}\theta\ \text{sen} ^{2}\phi +\rho ^{2}\text{ sen}^{2}\ \theta\ \text{sen} ^{2}\phi +\rho ^{2}\cos ^{2}\phi &=&a^{2} \\ \rho ^{2} \text{sen} ^{2}\phi +\rho ^{2}\cos ^{2}\phi &=&a^{2} \\ \rho ^{2} &=&a^{2} \\ \rho &=&a. \end{eqnarray*} La región \begin{equation*} W_{1}=\left\{ \left( \rho ,\theta ,\phi \right) \,\left\vert \,0\leq \rho \leq a,\quad 0\leq \theta \leq 2\pi ,\quad 0\leq \phi \leq \pi \right. \right\} \end{equation*} es del tipo I en el sistema \(\rho \Theta \Phi \) y está formada por las coordenadas esféricas de los puntos de \(W. \)

     Así, la transformación de coordenadas esféricas \(T_{e} \) transforma la caja \(W_{1}=\left[ 0,a\right] \times \left[ 0,2\pi \right] \times \left[ 0,\pi \right] \) en la esfera con centro en el origen de radio \( a \) :

      

      

      

     

      

      

      

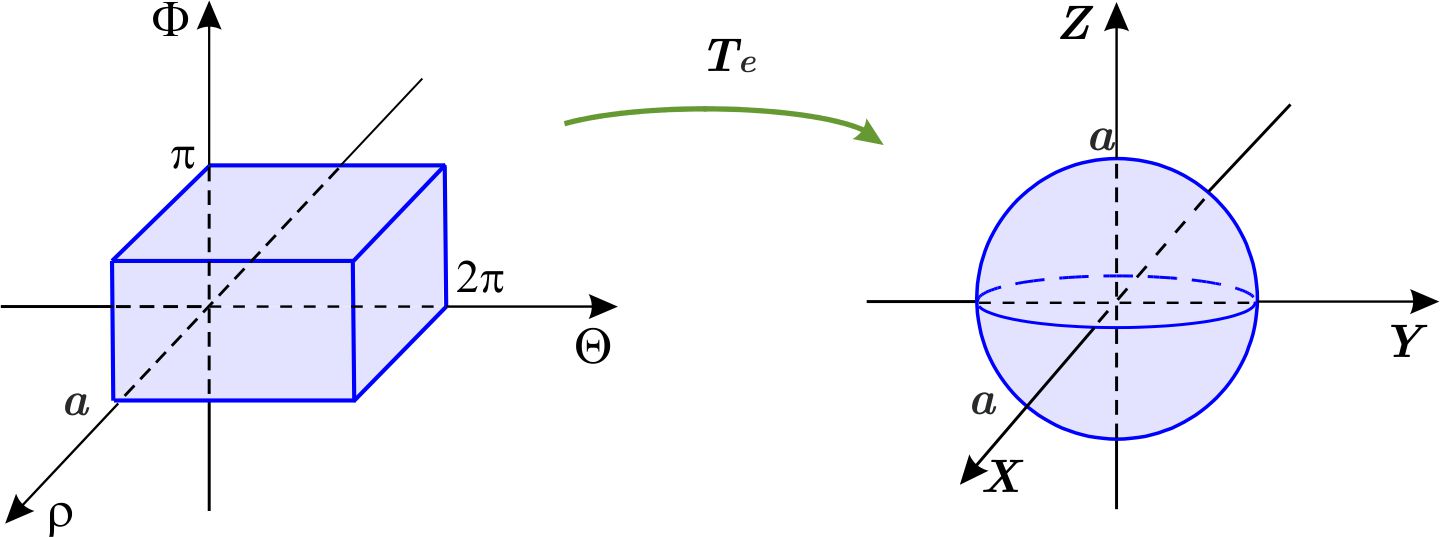
     Sabemos que el jacobiano de la transformación esférica es \(\dfrac{ \partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) } =-\rho ^{2} \text{sen}\ \phi . \)

     Aplicamos el Teorema de cambio de variables. \begin{eqnarray*} \text{Vol }W &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }\right\vert d\rho \,d\theta \,d\phi \text{ } \\ &=&\int_{0}^{2\pi }\int_{0}^{\pi }\int_{0}^{a}\rho ^{2} \text{sen}\ \phi \,d\rho \,d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{\pi }\left. \dfrac{\rho ^{3} }{3} \text{sen}\ \phi \right\vert _{0}^{a}d\phi \,d\theta \\ &=&\dfrac{a^{3}}{3}\int_{0}^{2\pi }\int_{0}^{\pi } \text{sen}\ \phi \,d\phi \,d\theta \\ &=&\dfrac{a^{3}}{3}\int_{0}^{2\pi }\left. -\cos \phi \right\vert _{0}^{\pi }\,d\theta \\ &=&\dfrac{a^{3}}{3}\int_{0}^{2\pi }2\,d\theta \\ &=&\dfrac{2a^{3}}{3}\left( 2\pi \right) \\ &=&\dfrac{4}{3}\pi a^{3}. \end{eqnarray*}

2. Encontrar el volumen del sólido \(W \) situado dentro del cono con ecuación \(z^{2}=x^{2}+y^{2} \) y de la esfera \(x^{2}+y^{2}+\left( z-4\right) ^{2}=16. \)

    

   Solución:

    

   Para calcular el volumen, escribiremos la integral en coordenadas cartesianas, cilíndricas y esféricas. Solamente calcularemos la que resulta más fácil.

   • Coordenadas cartesianas.

      

      

      

     

      

      

      

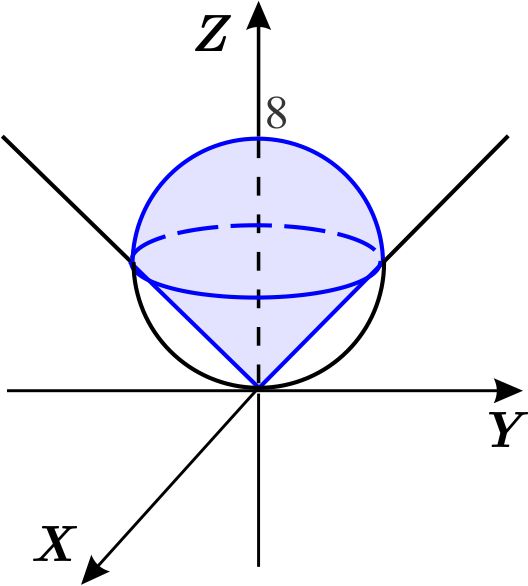
     Para encontrar la intersección del cono y la esfera, sustituimos \( z^{2}=x^{2}+y^{2} \) en la ecuación de la esfera: \begin{eqnarray*} z^{2}+\left( z-4\right) ^{2} &=&16 \\ 2z^{2}-8z+16 &=&16 \\ 2z\left( z-4\right) &=&0, \end{eqnarray*} de donde \(z=0 \) o \(z=4. \) Así el cono y la esfera se cortan en el origen y en \begin{equation*} 4^{2}=x^{2}+y^{2}, \end{equation*} es decir, en el círculo con centro en \(\left( 0,0,4\right) \) y radio \( 4, \) en el plano \(z=4. \)

     En coordenadas cartesianas describiremos la región \(W \) como de tipo I.

     La proyección \(D \) de \(W \) sobre el plano \(XY \) coincide con la del disco anterior, de manera que \(D \) es el círculo con centro en el origen, de radio \(4 \) , es decir \begin{equation*} D=\left\{ \left( x,y\right) \left\vert \,-4\leq x\leq 4,\quad -\sqrt{16-x^{2} }\leq y\leq \sqrt{16-x^{2}}\right. \right\} . \end{equation*} Para ver como varía \(z \) , despejamos \(z \) de las ecuaciones del cono y la esfera: \begin{eqnarray*} z^{2} &=&x^{2}+y^{2} \\ z &=&\sqrt{x^{2}+y^{2}} \end{eqnarray*} consideramos \(z\geq 0 \) ya que todos los puntos del esfera tienen coordenada \( z \) no negativa, y \begin{eqnarray*} x^{2}+y^{2}+\left( z-4\right) ^{2} &=&16 \\ \left( z-4\right) ^{2} &=&16-\left( x^{2}+y^{2}\right) \\ \left\vert z-4\right\vert &=&\sqrt{16-\left( x^{2}+y^{2}\right) } \\ z-4 &=&\sqrt{16-\left( x^{2}+y^{2}\right) } \\ z &=&4+\sqrt{16-\left( x^{2}+y^{2}\right) } \end{eqnarray*} consideramos que \(z-4\geq 0 \) ya que los puntos de la esfera dentro del cono son los de la semiesfera superior.

     La región está limitada, por abajo por el cono con ecuación \(z= \sqrt{x^{2}+y^{2}} \) y por arriba, por la semiesfera superior \(z=4+\sqrt{ 16-\left( x^{2}+y^{2}\right) }. \)

     Entonces \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\quad \sqrt{x^{2}+y^{2}}\leq z\leq 4+\sqrt{16-\left( x^{2}+y^{2}\right) }\right. \right\} . \end{equation*} O sea, \begin{equation*} W=\left\{ \left( x,y,z\right) \left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}},\quad \sqrt{x^{2}+y^{2}}\leq z\leq 4+ \sqrt{16-\left( x^{2}+y^{2}\right) }\right. \right\} . \end{equation*} El volumen se calcula como \begin{equation*} \text{Vol }W=\int_{-4}^{4}\int_{-\sqrt{16-x^{2}}}^{\sqrt{ 16-x^{2}}}\int_{\sqrt{x^{2}+y^{2}}}^{4+\sqrt{16-\left( x^{2}+y^{2}\right) }}dz\,dy\,dx. \end{equation*}

   • Coordenadas cilíndricas

     Escribimos el círculo \(D \) en coordenadas polares \begin{equation*} r^{2}\leq 16, \end{equation*} entonces \begin{equation*} D_{1}=\left\{ \left( r,\theta \right) \,\left\vert \,0\leq r\leq 4,\quad 0\leq \theta \leq 2\pi \right. \right\} \end{equation*} y escribimos las ecuaciones de las superficies en coordenadas cilíndricas: \begin{eqnarray*} z &=&\sqrt{x^{2}+y^{2}} \\ &=&\sqrt{r^{2}} \\ &=&r \end{eqnarray*} y \begin{eqnarray*} z &=&4+\sqrt{16-\left( x^{2}+y^{2}\right) } \\ &=&4+\sqrt{16-r^{2}}. \end{eqnarray*} De donde, \begin{equation*} W_{1}=\left\{ \left( r,\theta ,z\right) \,\left\vert 0\leq r\leq 4,\quad 0\leq \theta \leq 2\pi ,\quad r\leq z\leq 4+\sqrt{16-r^{2}}\right. \right\} \end{equation*} es una región del tipo I en el sistema \(R\Theta Z \) y está formada por las coordenadas cilíndricas de los puntos de \(W. \) Por tanto, su imagen bajo la transformación cilíndrica es \(W \) .

      

      

      

     

      

      

      

     Entonces el volumen de \(W \) se calcula como \begin{equation*} \text{Vol }W=\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }\right\vert dr\,d\theta \,dz=\int_{0}^{4}\int_{0}^{2\pi }\int_{r}^{4+\sqrt{16-r^{2}}}rdz\,d\theta \,dr. \end{equation*} Observamos que la proyección de la región \(W_{1} \) en el plano \(RZ \) es:

      

      

      

     

      

      

      

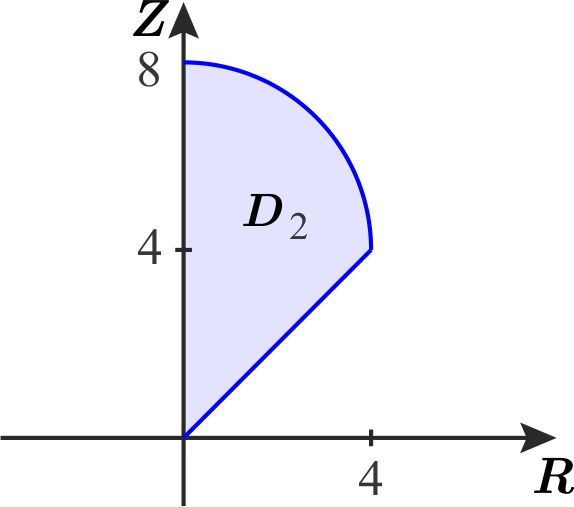
     A partir de la figura, notamos que para calcular el volumen de \(W \) , podemos hacer un cambio en el orden de integración. Dependiendo de si describimos la región de la figura anterior como de tipo \(1 \) o \(2 \) , tendremos que el orden en el que calcularemos la integral será \(d\theta \,dz\,dr \) o \(d\theta \,dr\,dz, \) respectivamente. Es decir:

     Si \(D_{2} \) se escribe como de tipo \(1 \) , se tiene: \begin{equation*} D_{2}=\left\{ \left( r,z\right) \,\left\vert \,0\leq r\leq 4,\quad r\leq z\leq 4+\sqrt{16-r^{2}}\right. \right\} , \end{equation*} de donde \begin{equation*} \text{Vol }W=\int_{0}^{4}\int_{r}^{4+\sqrt{16-r^{2}} }\int_{0}^{2\pi }rd\theta \,dz\,dr. \end{equation*} Si \(D_{2} \) se escribe como de tipo \(2 \) , se tiene: \begin{equation*} D_{2}=\left\{ \left( r,z\right) \,\left\vert \,0\leq z\leq 8,\quad 0\leq r\leq f\left( z\right) \right. \right\} , \end{equation*} donde \begin{equation*} f\left( z\right) =\left\{ \begin{array}{lcl} z & & \text{si }0\leq z\leq 4\text{ } \\ & & \\ \sqrt{16-\left( z-4\right) ^{2}} & & \text{si }4\leq z\leq 8\text{ } \end{array} \right. , \end{equation*} es decir, \begin{equation*} D_{2}=\left\{ \left( r,z\right) \,\left\vert \,0\leq z\leq 4,\quad 0\leq r\leq z\right. \right\} \cup \left\{ \left( r,z\right) \,\left\vert \,4\leq z\leq 8,\quad 0\leq r\leq \sqrt{16-\left( z-4\right) ^{2}}\right. \right\} . \end{equation*} Por tanto, \begin{equation*} \text{Vol }W=\int_{0}^{4}\int_{0}^{z}\int _{0}^{2\pi }rd\theta \,dr\,dz+\int_{4}^{8}\int_{r}^{\sqrt{16-\left( z-4\right) ^{2}}}\int_{0}^{2\pi }rd\theta \,dr\,dz. \end{equation*}

   • Coordenadas esféricas.

     Escribimos las ecuaciones del cono y de la esfera en coordenadas esféricas:

     El cono se escribe, en coordenadas esféricas como: \begin{eqnarray*} z^{2} &=&x^{2}+y^{2} \\ \rho ^{2}\cos ^{2}\phi &=&\rho ^{2}\cos ^{2}\theta\ \text{sen} ^{2}\phi +\rho ^{2} \text{sen} ^{2}\theta\ \text{sen} ^{2}\phi \\ \rho ^{2}\cos ^{2}\phi &=&\rho ^{2} \text{sen} ^{2}\phi \\ 1 &=&\dfrac{ \text{sen} ^{2}\phi }{\cos ^{2}\phi } \\ 1 &=&\tan ^{2}\phi \end{eqnarray*} y como \(0\leq \phi \leq \pi \) entonces \(\phi =\dfrac{\pi }{4}. \) De manera que \(\phi \in \left[ 0,\dfrac{\pi }{4}\right] . \)

     La ecuación en coordenadas esféricas, de la esfera es: \begin{eqnarray*} x^{2}+y^{2}+\left( z-4\right) ^{2} &=&16 \\ \rho ^{2}\cos ^{2}\theta\ \text{sen} ^{2}\phi +\rho ^{2}\text{ sen}^{2}\theta\ \text{sen} ^{2}\phi +\left( \rho \cos \phi -4\right) ^{2} &=&16 \\ \rho ^{2} \text{sen} ^{2}\phi +\rho ^{2}\cos ^{2}\phi -8\rho \cos \phi +16 &=&16 \\ \rho ^{2}-8\rho \cos \phi &=&0 \\ \rho \left( \rho -8\cos \phi \right) &=&0, \end{eqnarray*} de donde \begin{eqnarray*} \rho -8\cos \phi &=&0 \\ \rho &=&8\cos \phi . \end{eqnarray*} Observamos que no hay restricción para \(\theta , \) entonces \(\theta \in \left[ 0,2\pi \right] . \)

     La región \begin{equation*} W_{1}=\left\{ \left( \rho ,\theta ,\phi \right) \left\vert \,0\leq \theta \leq 2\pi ,\quad 0\leq \phi \leq \dfrac{\pi }{4},\quad 0\leq \rho \leq 8\cos \phi \right. \right\} \end{equation*} es del tipo I en el sistema \(\rho \Theta \Phi . \) Está formada por las coordenadas esféricas de los puntos de \(W. \) Por tanto, su imagen bajo la transformación esférica es \(W \) .

      

      

      

     

      

      

      

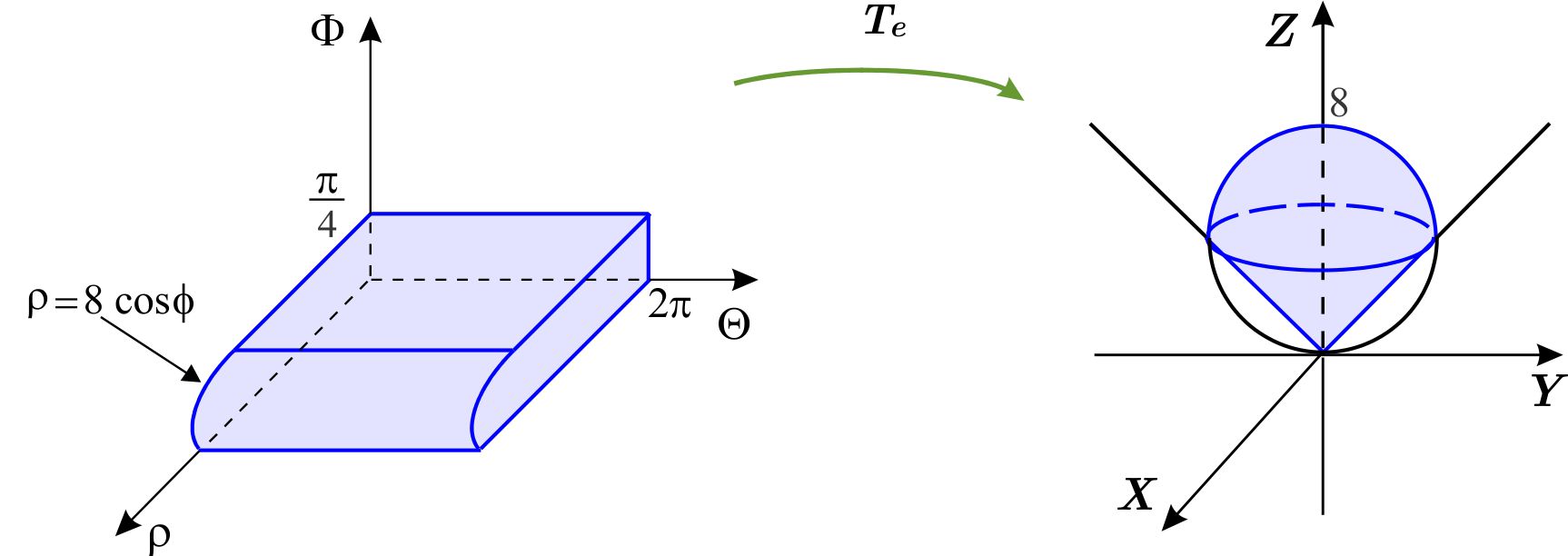
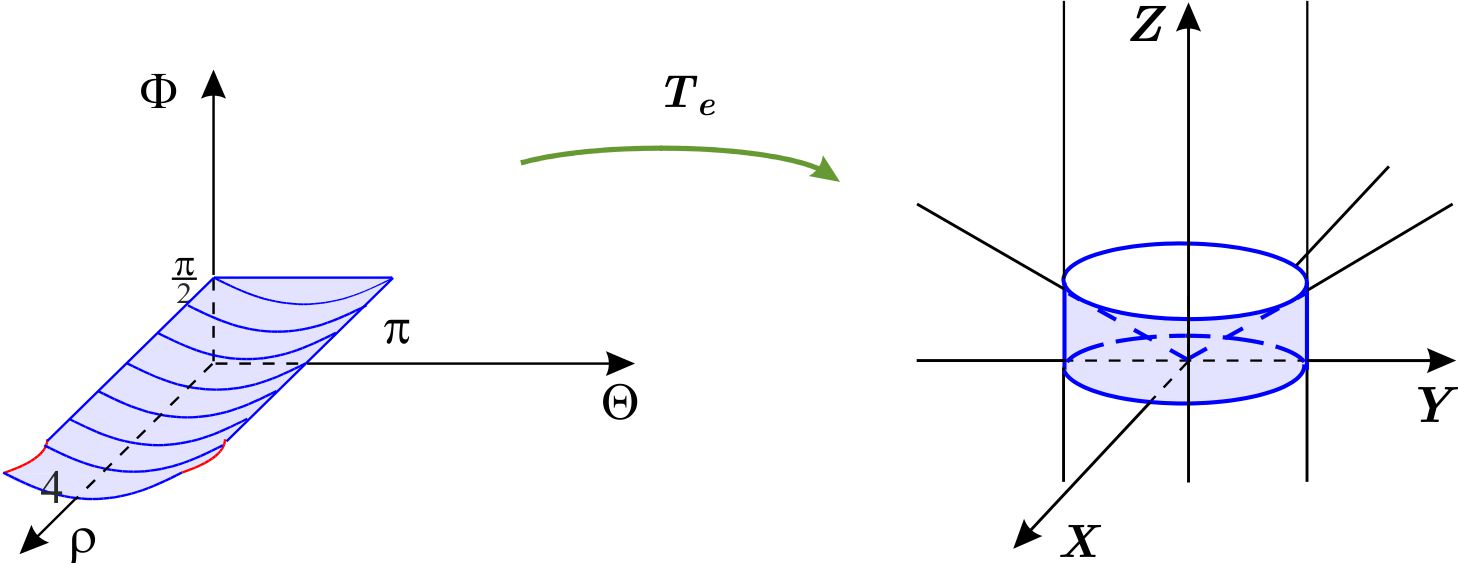
     El jacobiano de la transformación es \begin{equation*} \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }=-\rho ^{2} \text{sen}\ \phi , \end{equation*} entonces el volumen buscado es \begin{eqnarray*} \text{Vol }W &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }\right\vert d\rho \,d\theta \,d\phi \\ &=&\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{4} }\int_{0}^{8\cos \phi }\rho ^{2} \text{sen}\ \phi \,d\rho \,d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{4}}\left. \dfrac{\rho ^{3}}{3} \text{sen}\ \phi \right\vert _{0}^{8\cos \phi }d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{4}}\dfrac{1}{3} \left( 8\cos \phi \right) ^{3} \text{sen}\ \phi \,d\phi \,d\theta \\ &=&\dfrac{8^{3}}{3}\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{ 4}}\cos ^{3}\phi\ \text{sen}\ \phi \,d\phi \,d\theta \\ &=&\dfrac{8^{3}}{3}\int_{0}^{2\pi }\left. -\dfrac{1}{4}\cos ^{4}\phi \right\vert _{0}^{\frac{\pi }{4}}d\theta \\ &=&-\dfrac{8^{3}}{3\left( 4\right) }\int_{0}^{2\pi }\left( \dfrac{1 }{\sqrt{2}}\right) ^{4}-1d\theta \\ &=&-\dfrac{8^{3}}{3\left( 4\right) }\int_{0}^{2\pi }-\dfrac{3}{4} d\theta \\ &=&\dfrac{8^{3}3}{3\left( 4\right) 4}2\pi \\ &=&64\pi . \end{eqnarray*} Se puede utilizar la siguiente figura para cambiar el orden de integración:

      

      

      

     

      

      

      

3. Calcular \(\iiint_{W}x^{2}+y^{2}\,dx\,dy\,dz \) donde \(W \) es la región que se encuentra acotada por el cilindro \(x^{2}+y^{2}-16=0, \) abajo por \(z=0 \) y arriba por el paraboloide \(4z=x^{2}+y^{2}. \)

    

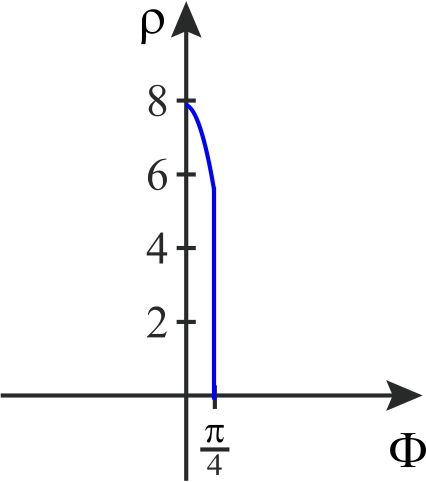
   Solución:

    

   Escribiremos la integral en coordenadas cartesianas, cilíndricas y esf éricas. Solamente calcularemos la que resulta más fácil.

   • Coordenadas cartesianas.

      

      

      

     

      

      

      

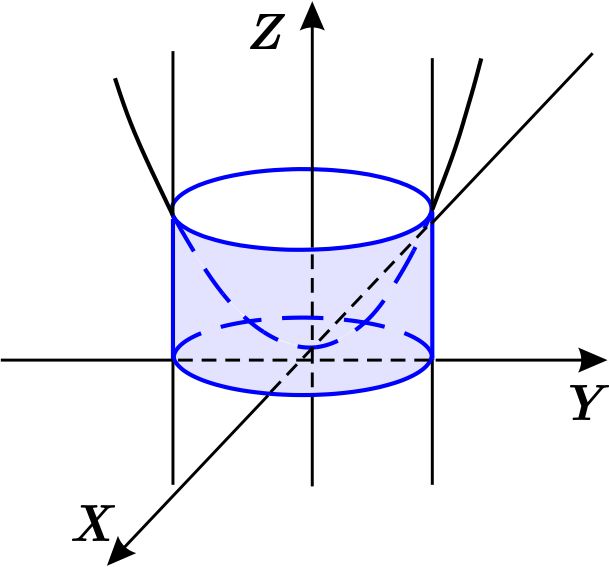
     En coordenadas cartesianas describiremos la región \(W \) como de tipo I.

     El cilindro tiene ecuación \begin{equation*} x^{2}+y^{2}=16 \end{equation*} y el paraboloide: \begin{equation*} z=\dfrac{x^{2}+y^{2}}{4}. \end{equation*} Sustituimos \(x^{2}+y^{2} \) en la ecuación del paraboloide \begin{equation*} z=\dfrac{x^{2}+y^{2}}{4}=\dfrac{16}{4}=4. \end{equation*} Es decir, el cilindro y el paraboloide se cortan en \(z=4. \) Es decir, en el círculo con centro en \(\left( 0,0,4\right) \) y radio \(4 \) en el plano \( z=4. \)

     La proyección \(D \) de \(W \) sobre el plano \(XY \) coincide con la del círculo anterior, de manera que \(D \) es el círculo con centro en el origen, de radio \(4 \) , es decir \begin{equation*} x^{2}+y^{2}\leq 16 \end{equation*} que es una región de tipo 3 en el plano, podemos escribir, describiéndola como de tipo 1.

     Así, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}}\right. \right\} , \end{equation*} de donde \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}},\quad 0\leq z\leq \dfrac{x^{2}+y^{2}}{4} \right. \right\} . \end{equation*} De manera que \begin{equation*} \iiint_{W}x^{2}+y^{2}\,dx\,dy\,dz=\int_{-4}^{4}\int _{-\sqrt{16-x^{2}}}^{\sqrt{16-x^{2}}}\int_{0}^{\frac{1}{4} \left( x^{2}+y^{2}\right) }x^{2}+y^{2}\,dz\,dy\,dx. \end{equation*}

   • Coordenadas cilíndricas.

     El cilindro \(x^{2}+y^{2}=16 \) se describe en coordenadas cilíndricas como: \begin{eqnarray*} x^{2}+y^{2} &=&16 \\ r^{2} &=&16 \\ r &=&4. \end{eqnarray*} Escribimos la ecuación del paraboloide en coordenadas cilíndricas: \begin{eqnarray*} z &=&\dfrac{x^{2}+y^{2}}{4} \\ &=&\dfrac{r^{2}\cos ^{2}\theta +r^{2} \text{sen} ^{2}\theta }{4} \\ &=&\dfrac{r^{2}}{4}. \end{eqnarray*} Entonces las superficies que acotan la región son \begin{equation*} z=0\quad \quad \quad \text{y} \quad \quad \quad z=\dfrac{r^{2}}{4}, \end{equation*} de donde, \begin{equation*} W_{1}=\left\{ \left( r,\theta ,z\right) \,\left\vert \,0\leq r\leq 4,\quad 0\leq \theta \leq 2\pi ,\quad 0\leq z\leq \dfrac{r^{2}}{4}\right. \right\} \end{equation*} es una región del tipo I en el sistema \(R\Theta Z \) y está formada por las coordenadas cilíndricas de los puntos de \(W. \) Por tanto, \( T_{c}\left( W_{1}\right) =W \) .

     Así,

      

      

      

     

      

      

      

     La integral es: \begin{eqnarray*} \iiint_{W}x^{2}+y^{2}\,dx\,dy\,dz &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{ \partial \left( r,\theta ,z\right) }\right\vert dr\,d\theta \,dz\text{ } \\ &=&\iiint_{W_{1}}\left( r^{2}\cos ^{2}\theta +r^{2} \text{sen} ^{2}\theta \right) r\,dr\,d\theta \,dz \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\int_{0}^{\frac{ r^{2}}{4}}\left( r^{2}\cos ^{2}\theta +r^{2} \text{sen} ^{2}\theta \right) r\,dz\,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\int_{0}^{\frac{ r^{2}}{4}}r^{3}dz\,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\left. zr^{3}\right\vert _{0}^{\frac{r^{2}}{4}}dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\dfrac{r^{5}}{4} dr\,d\theta \, \\ &=&\dfrac{1}{4}\int_{0}^{2\pi }\left. \dfrac{r^{6}}{6}\right\vert _{0}^{4}d\theta \\ &=&\dfrac{4^{6}}{24}\int_{0}^{2\pi }d\theta \\ &=&\dfrac{512}{3}\left( 2\pi \right) \\ &=&\dfrac{1024}{3}\pi . \end{eqnarray*}

   • Coordenadas esféricas

     Encontramos la ecuación del cilindro en coordenadas esféricas: \begin{eqnarray*} x^{2}+y^{2} &=&16 \\ \rho ^{2} \text{sen} ^{2}\phi \cos ^{2}\theta +\rho ^{2}\text{sen}^{2}\phi\ \text{sen} ^{2}\theta &=&16 \\ \rho ^{2} \text{sen} ^{2}\phi \left( \cos ^{2}\theta + \text{sen} ^{2}\theta \right) &=&16 \\ \rho ^{2} \text{sen} ^{2}\phi &=&16 \\ \rho\ \text{sen}\ \phi &=&4\text{ ya que }\rho \geq 0\text{ y }\phi \in \left[ 0,\pi \right] \\ \rho &=&\dfrac{4}{ \text{sen}\ \phi }. \end{eqnarray*} Obtenemos la ecuación del paraboloide en coordenadas esféricas: \begin{eqnarray*} z &=&\dfrac{x^{2}+y^{2}}{4} \\ \rho \cos \phi &=&\dfrac{\rho ^{2} \text{sen} ^{2}\phi }{4} \\ 4\cos \phi &=&\rho\ \text{sen} ^{2}\phi \\ \rho &=&\dfrac{4\cos \phi }{ \text{sen} ^{2}\phi }. \end{eqnarray*} Puesto que el cilindro y el paraboloide se cortan en \(z=4, \) los puntos de la intersección, \(\left( x,y,z\right) \) tienen coordenadas esféricas \( \left( \rho ,\theta ,\phi \right) \) tales que \begin{equation*} \rho \cos \phi =4, \end{equation*} de donde, \begin{equation*} \rho =\dfrac{4}{\cos \phi }. \end{equation*} Entonces \begin{equation*} \left( x,y,z\right) =\left( \dfrac{4}{\cos \phi } \text{sen}\ \phi \cos \theta ,\dfrac{4}{\cos \phi }\ \text{sen}\ \phi\ \text{sen}\ \theta ,\dfrac{4 }{\cos \phi }\cos \phi \right) =\left( 4\tan \phi \cos \theta ,4\tan \phi \ \text{sen}\ \theta ,4\right) . \end{equation*} Como estos puntos están también en el cilindro: \begin{eqnarray*} 16\tan ^{2}\phi \cos ^{2}\theta +16\tan ^{2}\phi\ \text{sen} ^{2}\theta &=&16 \\ \tan ^{2}\phi \left( \cos ^{2}\theta + \text{sen} ^{2}\theta \right) &=&1 \\ \tan ^{2}\phi &=&1 \end{eqnarray*} y puesto que la región se encuentra en el semiplano positivo, tenemos que \begin{eqnarray*} \tan \phi &=&1 \\ \phi &=&\dfrac{\pi }{4}. \end{eqnarray*} Por otra parte, el plano \(XY \) tiene ecuación, en coordenadas esféricas: \(\phi =\dfrac{\pi }{2}. \) De donde, \begin{equation*} W_{1}=\left\{ \left( \rho ,\theta ,\phi \right) \left\vert \,0\leq \theta \leq 2\pi ,\quad \dfrac{\pi }{4}\leq \phi \leq \dfrac{\pi }{2},\quad \dfrac{ 4\cos \phi }{ \text{sen} ^{2}\phi }\leq \rho \leq \dfrac{4}{ \text{sen}\ \phi }\right. \right\} \end{equation*} es una región del tipo I en el sistema \(\rho \Theta \Phi \) y está formada por las coordenadas esféricas de los puntos de \(W. \) Por tanto, su imagen bajo la transformación esférica \(T_{e} \) es \(W \) .

      

      

      

     

      

      

      

     La integral que se debe calcular es: \begin{eqnarray*} \iiint_{W}x^{2}+y^{2}\,dx\,dy\,dz &=&\iiint_{W_{1}}\rho ^{2} \text{sen} ^{2}\phi \left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }\right\vert d\rho \,d\theta \,d\phi \text{ } \\ &=&\int_{0}^{2\pi }\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}\int_{\frac{ 4\cos \phi }{ \text{sen} ^{2}\phi }}^{\frac{4}{ \text{sen}\ \phi } }\rho ^{2} \text{sen} ^{2}\phi \left( \rho ^{2} \text{sen} ^{2}\phi \right) \,d\rho \,d\phi \,d\theta \\ &=&\int_{0}^{2\pi }\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}\int_{\frac{ 4\cos \phi }{ \text{sen} ^{2}\phi }}^{\frac{4}{ \text{sen}\ \phi } }\rho ^{4} \text{sen} ^{4}\phi \,d\rho \,d\phi \,d\theta . \end{eqnarray*}

4. Calcular \(\iiint_{W}\,dx\,dy\,dz \) donde \(W \) es la región acotada arriba por \(z=9 \) y abajo por el manto superior del cono de dos mantos \(z^{2}=x^{2}+y^{2}. \)

    

   Solución:

    

   Escribiremos la integral en coordenadas cartesianas, cilíndricas y esféricas. Solamente calcularemos la que resulta más fácil.

   • Coordenadas cartesianas.

      

      

      

     

      

      

      

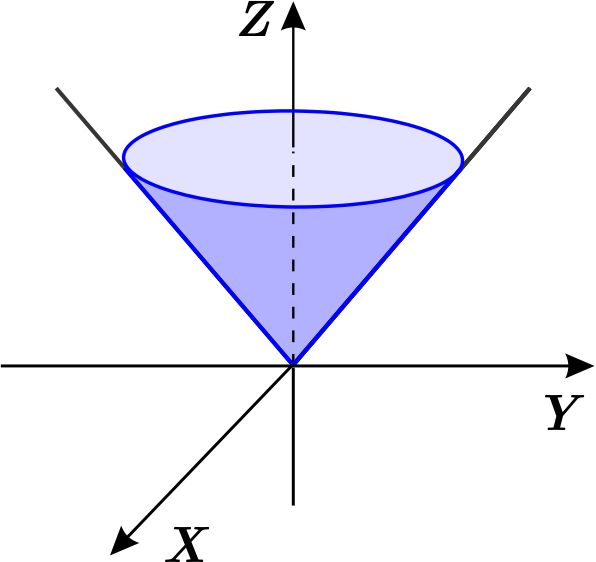
     En coordenadas cartesianas describiremos la región \(W \) como de tipo II.

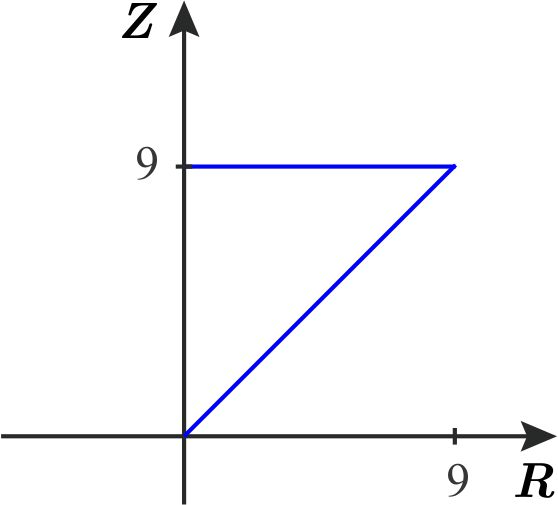
     Proyectando \(W \) en el plano \(YZ \) obtenemos la región \(D \) definida por la inecuación \begin{eqnarray*} z^{2} &\geq &y^{2} \\ z &\geq &\left\vert y\right\vert \end{eqnarray*} con \(0\leq z\leq 9. \)

     Despejamos \(x \) de \begin{eqnarray*} x^{2}+y^{2} &=&z^{2} \\ x^{2} &=&z^{2}-y^{2} \\ \left\vert x\right\vert &=&\sqrt{z^{2}-y^{2}}. \end{eqnarray*} Así \begin{equation*} W=\left\{ \left( r,\theta ,z\right) \left\vert \,0\leq z\leq 9,\quad -z\leq y\leq z,\quad -\sqrt{z^{2}-y^{2}}\leq x\leq \sqrt{z^{2}-y^{2}}\right. \right\} . \end{equation*} Entonces \begin{equation*} \iiint_{W}\,dx\,dy\,dz=\int_{0}^{9}\int_{-z}^{z}\int_{-\sqrt{ z^{2}-y^{2}}}^{\sqrt{z^{2}-y^{2}}}dx\,dy\,dz. \end{equation*}

   • Coordenadas cilíndricas.

     Las superficies que acotan la región superior e inferiormente se escriben en coordenadas cilíndricas como: \begin{equation*} z=9 \end{equation*} y \begin{eqnarray*} z^{2} &=&x^{2}+y^{2} \\ z^{2} &=&r^{2} \\ z &=&r. \end{eqnarray*} De donde, \begin{equation*} W_{1}=\left\{ \left( r,\theta ,z\right) \,\left\vert \,0\leq r\leq 9,\quad 0\leq \theta \leq 2\pi ,\quad r\leq z\leq 9\right. \right\} \end{equation*} es una región del tipo I en el sistema \(R\Theta Z \) y está formada por las coordenadas cilíndricas de los puntos de \(W. \) Por tanto, \( T_{c}\left( W_{1}\right) =W \) . Así,

      

      

      

     

      

      

      

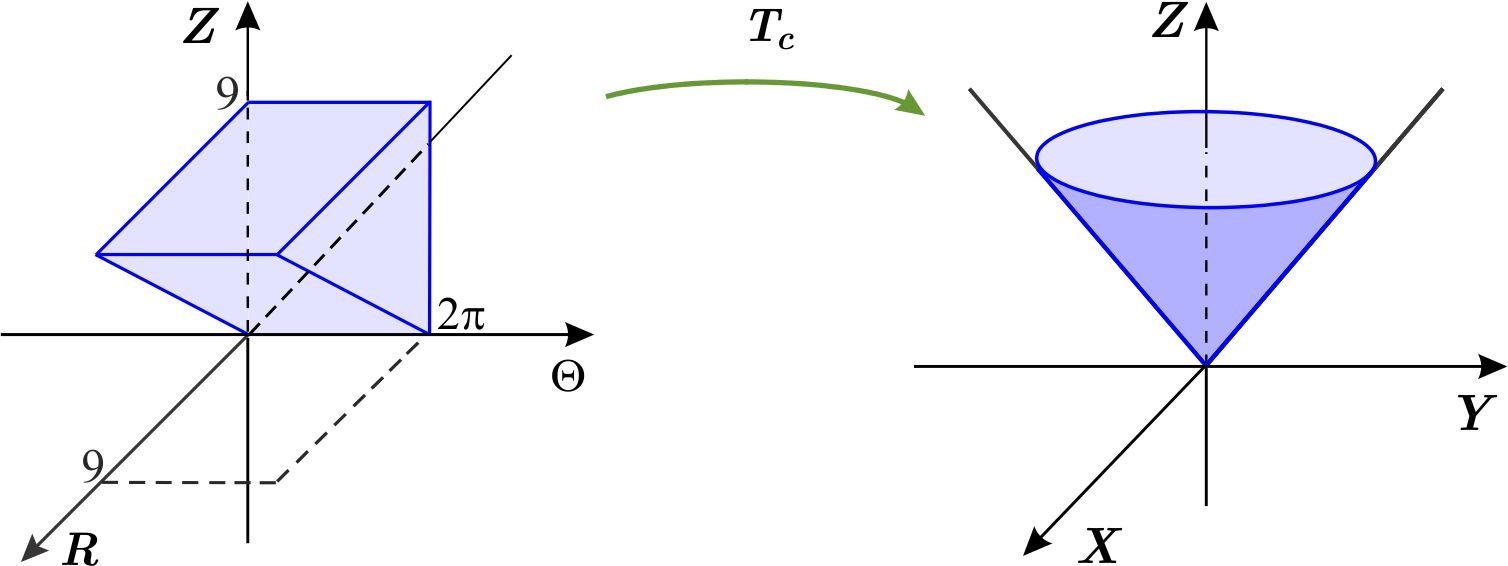
     de donde \begin{eqnarray*} \iiint_{W}\,dx\,dy\,dz &=&\iiint_{W_{1}}\left\vert \dfrac{ \partial \left( x,y,z\right) }{\partial \left( r,\theta ,z\right) } \right\vert dr\,d\theta \,dz\text{ } \\ &=&\int_{0}^{9}\int_{0}^{2\pi }\int_{r}^{9}rdz\,d\theta \,dr. \end{eqnarray*} Calculamos esta integral \begin{eqnarray*} \iiint_{W}\,dx\,dy\,dz &=&\iiint_{W_{1}}\left\vert \dfrac{ \partial \left( x,y,z\right) }{\partial \left( r,\theta ,z\right) } \right\vert \,dr\,d\theta \,dz \\ &=&\int_{0}^{9}\int_{0}^{2\pi }\int_{r}^{9}r\,dz\,d\theta \,dr \\ &=&\int_{0}^{9}\int_{0}^{2\pi }\left. rz\right\vert _{r}^{9}\,d\theta \,dr \\ &=&\int_{0}^{9}\int_{0}^{2\pi }9r-r^{2}d\theta \,dr \\ &=&\int_{0}^{9}\left. \left( 9r-r^{2}\right) \theta \right\vert _{0}^{2\pi }\,dr \\ &=&\int_{0}^{9}2\pi \left( 9r-r^{2}\right) \,dr \\ &=&\left. 2\pi \left( \dfrac{9}{2}r^{2}-\dfrac{r^{3}}{3}\right) \right\vert _{0}^{9} \\ &=&2\pi \left( \dfrac{9}{2}\left( 81\right) -\dfrac{9^{3}}{3}\right) \\ &=&243\pi . \end{eqnarray*} Si se quiere hacer un cambio en el orden de integración, puede considerarse la región:

      

      

      

     

      

      

      

   • Coordenadas esféricas.

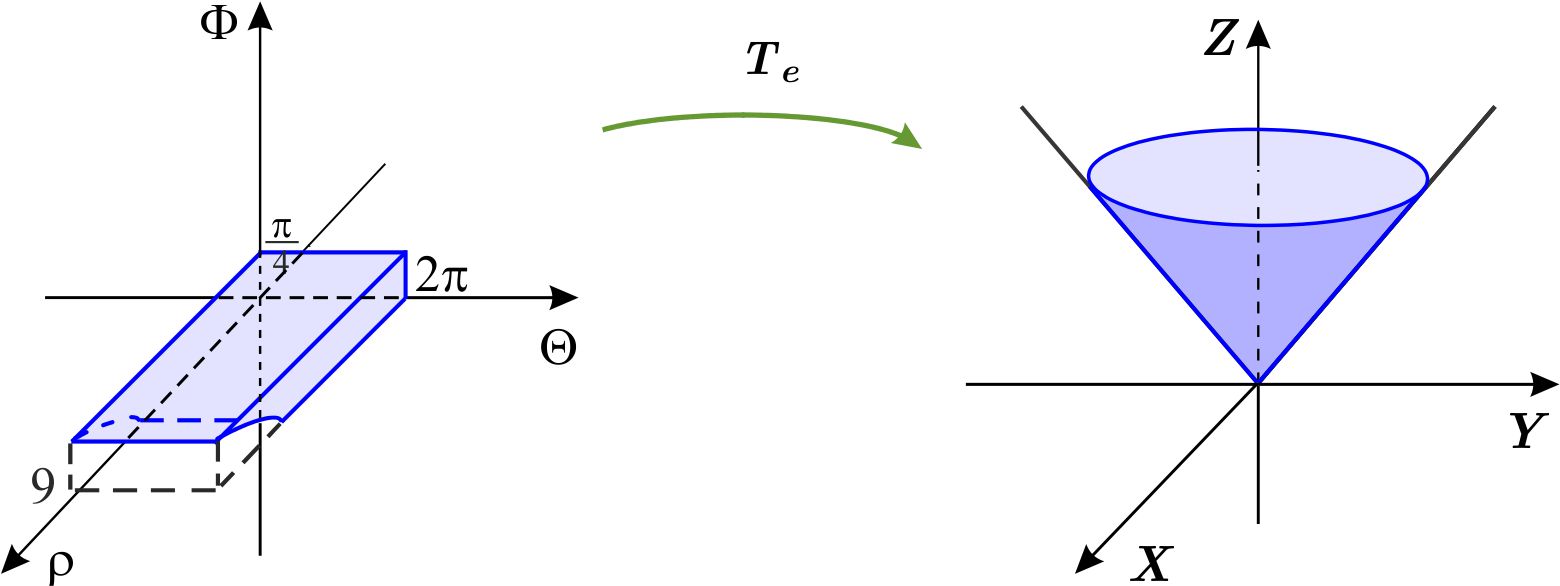
     Escribimos las ecuaciones de las superficies que acotan la región superior e inferiormente en coordenadas esféricas \begin{eqnarray*} z &=&9 \\ \rho \cos \phi &=&9 \\ \rho &=&\dfrac{9}{\cos \phi } \end{eqnarray*} y \begin{eqnarray*} z^{2} &=&x^{2}+y^{2} \\ \rho ^{2}\cos ^{2}\phi &=&\rho ^{2}\cos ^{2}\theta\ \text{sen} ^{2}\phi +\rho ^{2} \text{sen} ^{2}\theta\ \text{sen} ^{2}\phi \\ \rho ^{2}\cos ^{2}\phi &=&\rho ^{2} \text{sen} ^{2}\phi \\ 1 &=&\dfrac{ \text{sen} ^{2}\phi }{\cos ^{2}\phi } \\ 1 &=&\tan ^{2}\phi \\ \phi &=&\dfrac{\pi }{4}. \end{eqnarray*} Entonces \begin{equation*} W_{1}=\left\{ \left( \rho ,\theta ,\phi \right) \left\vert \,0\leq \theta \leq 2\pi ,\quad 0\leq \phi \leq \dfrac{\pi }{4},\quad 0\leq \rho \leq \dfrac{9}{\cos \phi }\right. \right\} \end{equation*} es una región del tipo I en el sistema \(\rho \Theta \Phi \) y está formada por las coordenadas esféricas de los puntos de \(W. \) Por tanto, \( T_{e}\left( W_{1}\right) =W \) . Así,

      

      

      

     

      

      

      

     De donde, \begin{eqnarray*} \iiint_{W}\,dx\,dy\,dz &=&\iiint_{W_{1}}\left\vert \dfrac{ \partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) } \right\vert d\rho \,d\theta \,d\phi \text{ } \\ &=&\int_{0}^{2\pi }\int_{0}^{\frac{\pi }{4} }\int_{0}^{\frac{9}{\cos \phi }}\rho ^{2} \text{sen}\ \phi \,d\rho \,d\phi \,d\theta . \end{eqnarray*}

5. Encontrar el volumen de la región \(W \) limitada por las superficies \( r^{2}=16, \) abajo por \(z=0 \) y arriba por el cono \(2z=\sqrt{x^{2}+y^{2}}. \)

    

   Solución:

    

   Calcularemos el volumen usando cilíndricas e indicaremos las integrales correspondientes usando coordenadas cartesianas y esféricas.

    

    

    

   

    

    

    

   • Coordenadas cartesianas.

     En coordenadas cartesianas describiremos la región \(W \) como de tipo I.

     Escribimos \(r^{2}=16 \) en coordenadas cartesianas \begin{eqnarray*} r^{2} &=&16 \\ x^{2}+y^{2} &=&16. \end{eqnarray*} La proyección \(D \) de \(W \) sobre el plano \(XY \) coincide con la del círculo anterior. Como la otra superficie es \begin{eqnarray*} 2z &=&\sqrt{x^{2}+y^{2}} \\ z &=&\dfrac{\sqrt{x^{2}+y^{2}}}{2}. \end{eqnarray*} Entonces \begin{equation*} W=\left\{ \left( x,y,z\right) \left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq -\sqrt{16-x^{2}},\quad 0\leq z\leq \dfrac{\sqrt{ x^{2}+y^{2}}}{2}\right. \right\} , \end{equation*} de donde \begin{equation*} \text{Vol }W=\int_{-4}^{4}\int_{-\sqrt{16-x^{2}}}^{\sqrt{ 16-x^{2}}}\int_{0}^{\frac{\sqrt{x^{2}+y^{2}}}{2}}dz\,dy\,dx. \end{equation*}

   • Coordenadas cilíndricas.

     Tenemos \begin{eqnarray*} r^{2} &=&16 \\ r &=&4. \end{eqnarray*} Escribimos la ecuación cilíndrica de la superficie \(2z=\sqrt{ x^{2}+y^{2}} \) que acota superiormente la región. Entonces \begin{eqnarray*} z &=&\dfrac{\sqrt{x^{2}+y^{2}}}{2} \\ &=&\dfrac{r}{2}. \end{eqnarray*} El conjunto \begin{equation*} W_{1}=\left\{ \left( r,\theta ,z\right) \left\vert \,0\leq \theta \leq 2\pi ,\quad \,0\leq r\leq 4,\,\quad 0\leq z\leq \dfrac{r}{2}\right. \right\} . \end{equation*} es una colección de coordenadas cilíndricas de \(W. \) Así \( T_{c}\left( W_{1}\right) =W, \) de donde,

      

      

      

     

      

      

      

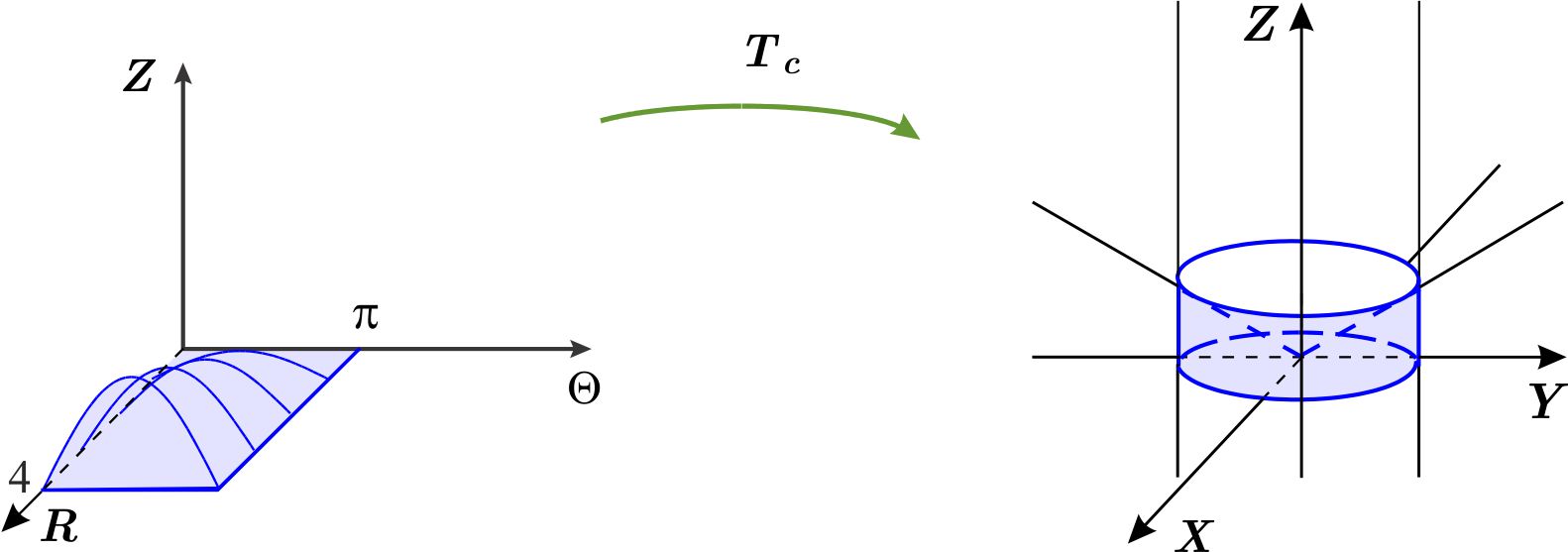
     \begin{eqnarray*} \text{Vol }W &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( r,\theta ,z\right) }\right\vert dr\,d\theta \,dz \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\int_{0}^{\frac{ r}{2}}r\,dz\,dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\left. rz\right\vert _{0}^{\frac{r}{2}}dr\,d\theta \\ &=&\int_{0}^{2\pi }\int_{0}^{4}\dfrac{r^{2}}{2} \,dr\,d\theta \\ &=&\int_{0}^{2\pi }\left. \dfrac{r^{3}}{6}\right\vert _{0}^{4}\,d\theta \\ &=&\dfrac{4^{3}}{6}\int_{0}^{2\pi }\,d\theta \\ &=&\dfrac{4^{3}}{6}\left( 2\pi \right) \\ &=&\dfrac{64}{3}\pi . \end{eqnarray*}

   • Coordenadas esféricas.

     Escribimos las ecuaciones en coordenadas esféricas \begin{eqnarray*} x^{2}+y^{2} &=&16 \\ \rho ^{2}\cos ^{2}\theta\ \text{sen} ^{2}\phi +\rho ^{2}\text{ sen}^{2}\theta\ \text{sen} ^{2}\phi &=&16 \\ \rho ^{2} \text{sen} ^{2}\phi &=&16 \\ \left\vert \rho\ \text{sen}\ \phi \right\vert &=&4, \end{eqnarray*} como \(\rho \geq 0 \) y \(0<\phi <\pi , \) entonces \(\rho\ \text{sen}\ \phi \geq 0, \) así \begin{eqnarray*} \rho\ \text{sen}\ \phi &=&4 \\ \rho &=&\dfrac{4}{ \text{sen}\ \phi } \end{eqnarray*} y \begin{eqnarray*} 2z &=&\sqrt{x^{2}+y^{2}} \\ 2\rho \cos \phi &=&\sqrt{\rho ^{2} \text{sen} ^{2}\phi } \\ 2\rho \cos \phi &=&\rho \left\vert \text{sen}\ \phi \right\vert \\ 2\rho \cos \phi &=&\rho\ \text{sen}\ \phi \quad \quad \quad \quad \text{ya que } 0\leq \phi \leq \pi \\ 2 &=&\tan \phi \\ \phi &=&\arctan \left( 2\right) . \end{eqnarray*} Si \begin{eqnarray*} z &=&0 \\ \rho \cos \phi &=&0, \end{eqnarray*} entonces \begin{eqnarray*} \cos \phi &=&0 \\ \phi &=&\dfrac{\pi }{2}. \end{eqnarray*} De donde \begin{equation*} W_{1}=\left\{ \left( \rho ,\theta ,\phi \right) \left\vert \,0\leq \theta \leq 2\pi ,\quad \arctan \left( 2\right) \leq \phi \leq \dfrac{\pi }{2} ,\quad 0\leq \rho \leq \dfrac{4}{ \text{sen}\ \phi }\right. \right\} . \end{equation*} Así,

      

      

      

     

      

      

      

     \begin{eqnarray*} \text{Vol }W &=&\iiint_{W_{1}}\left\vert \dfrac{\partial \left( x,y,z\right) }{\partial \left( \rho ,\theta ,\phi \right) }\right\vert d\rho \,d\theta \,d\phi \\ &=&\int_{0}^{2\pi }\int_{\arctan \left( 2\right) }^{ \frac{\pi }{2}}\int_{0}^{\frac{4}{ \text{sen}\ \theta }}\rho ^{2} \text{sen}\ \phi \,d\rho \,d\phi \,d\theta . \end{eqnarray*}

Ejercicios

1. Considera la región \(W \) que se encuentra en el primer octante, acotada por \(y=\sqrt{9-x^{2}} \) y \(z=4. \) Encuentra el volumen de la región usando:
   
   
   1. Coordenadas cartesianas, considerando el orden de integración \( dy\,dz\,dx. \)
   2. Coordenadas cilíndricas.
   3. Coordenadas esféricas.
   
   
   
2. Considera la región \(W \) que se encuentra dentro de \( x^{2}+y^{2}+z=8 \) sobre el plano \(z=4. \) Encuentra el volumen de la región usando:
   
   
   
   1. Coordenadas cartesianas, considerando el orden \(dy\,dz\,dx. \)
   2. Coordenadas cilíndricas.
   
   
   
3. Considera la región \(W \) acotada por abajo por el anillo \( x^{2}+y^{2}=4 \) y \(x^{2}+y^{2}=9 \) , en el plano \(XY, \) y por arriba por la esfera de radio \(3 \) :
   
   
   
   1. Encuentra el volumen de la región usando coordenadas cilíndricas.
   2. Verifica tu resultado considerando la diferencia del volumen de la semiesfera superior \(W_{2} \) menos el volumen de la región \(W_{3} \) acotada por el cilindro \(x^{2}+y^{2}=4, \) el plano \(XY \) y el hemisferio superior de la esfera de radio \(3 \) . Usa coordenadas cilíndricas.
   
   
   
4. Considera la región \(W \) acotada por abajo por el plano \(z=1 \) y arriba por la esfera \(x^{2}+y^{2}+z^{2}=4. \) Calcula el volumen de \(W \) usando coordenadas esféricas.
   
   
5. Considera el elipsoide \(E \) definido por \(\dfrac{x^{2}}{9}+\dfrac{y^{2} }{16}+\dfrac{z^{2}}{25}\leq 1. \) Encuentra el volumen de \(E \) siguiendo las instrucciones:
   1. Haz el cambio de variables \(u=\dfrac{x}{3},v=\dfrac{y}{4},w=\dfrac{ z}{5} \) encuentra la región en el sistema \(UVW \) sobre la que hay que integrar para calcular el volumen y deja indicada la integral.
   2. Calcula la integral resultante usando coordenadas esféricas.
   
   
   
6. Considera la región \(W \) que se encuentra dentro de la esfera \( x^{2}+y^{2}+z^{2}=4 \) y sobre el manto inferior del cono \(\left( z-2\right) ^{2}=x^{2}+y^{2}. \) Encuentra el volumen de \(W. \)
   1. Usando coordenadas cilíndricas.
   2. Verifica tu resultado considerando la diferencia de \(\dfrac{2}{3} \pi \left( 2^{3}\right) , \) el volumen del hemisferio superior de la esfera, menos el volumen de la región acotada por el manto inferior del cono \( \left( z-2\right) ^{2}=x^{2}+y^{2} \) y el plano \(XY \) .
   
   
   
7. Encuentra el volumen de la región acotada por las superficies \( \rho =1 \) y \(\rho =\dfrac{2}{\sqrt{3}}\cos \phi . \)