Integrales Triples

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Cambio en el orden de integración

En el cálculo de las integrales triples, como en el caso de las dobles, en ocasiones no es sencillo hacer el cálculo, pero un cambio en el orden de integración puede ayudarnos.

Para hacer el cambio de orden en las integrales dobles, la región \(D \) sobre la que vamos a integrar debe ser de tipo 3, es decir, debe poder escribirse como de tipo 1 y tipo 2.

En las triples, para poder hacer un cambio en el orden, la región \(W \) sobre la que va a integrarse, debe ser de al menos uno de los tipos I, II y III, de tal manera que la región \(D \) correspondiente sea de tipo \(3. \)

Dependiendo del tipo en el que se presenta la región \(W\subset \mathbb{R} ^{3}, \) determinamos la región plana \(D \) del tipo 1 o 2 en el plano correspondiente.

 

Por ejemplo:

 

Para presentar a una región \(W\subset \mathbb{R}^{3} \) como de tipo I, debemos determinar una región plana \(D \) del tipo 1 o tipo 2 en el plano \( XY \) . Para esto consideramos la proyección de \(W \) sobre el plano \(XY. \)

Una vez escrita la región \(W \) en \(\mathbb{R}^{3} \) de alguna de las formas anteriores, elegimos el orden en el que calcularemos la integral sobre la región \(W \). En cada tipo, dependiendo de si la región \(D \), proyección de \(W \), es de tipo \(1 \) o \(2, \) elegimos el orden para el cálculo de la integral:

 

Si la región \(W \) es:

Observación. En una integral triple, una vez establecido el orden, por ejemplo \(dx\,dy\,dz \) , notamos que al leer de izquierda a derecha, la primera variable que vemos es \(x, \) lo cual indica que se está considerando la proyección en el plano determinado por las otras dos, en este caso \(YZ. \)

Si una región \(W \) en \(\mathbb{R}^{3} \) es de los tres tipos anteriores, de manera que las proyecciones en cada uno de los planos \(XY,YZ \) y \(XZ \) son de tipo \(3, \) una integral sobre \(W \) puede escribirse en cualquiera de los seis órdenes siguientes: \begin{equation*} dz\,dy\,dx,\qquad dz\,dx\,dy,\qquad dx\,dz\,dy,\qquad dx\,dy\,dz,\qquad dy\,dz\,dx,\qquad \text{y}\qquad dy\,dx\,dz. \end{equation*}

 

Ejemplos.

 

  1. Considera la integral \[\int_{0}^{1}\int_{0}^{1-x} \int_{0}^{2}dz\,dy\,dx. \] Dibuja la región \(W \) cuyo volumen corresponde a la integral dada y escribe la integral en el orden \(dx\,dy\,dz \) .

     

    Solución:

     

    La proyección de \(W \) en el plano \(XY \) es \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,0\leq x\leq 1,\quad 0\leq y\leq 1-x\right. \right\} . \end{equation*} La región \(W \) está dada por \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\,\quad 0\leq z\leq 2\right. \right\} \\ W &=&\left\{ \left( x,y,z\right) \,\left\vert \,0\leq x\leq 1,\,\quad 0\leq y\leq 1-x,\,\quad 0\leq z\leq 2\right. \right\} \end{eqnarray*}

     

     

     

     

     

     

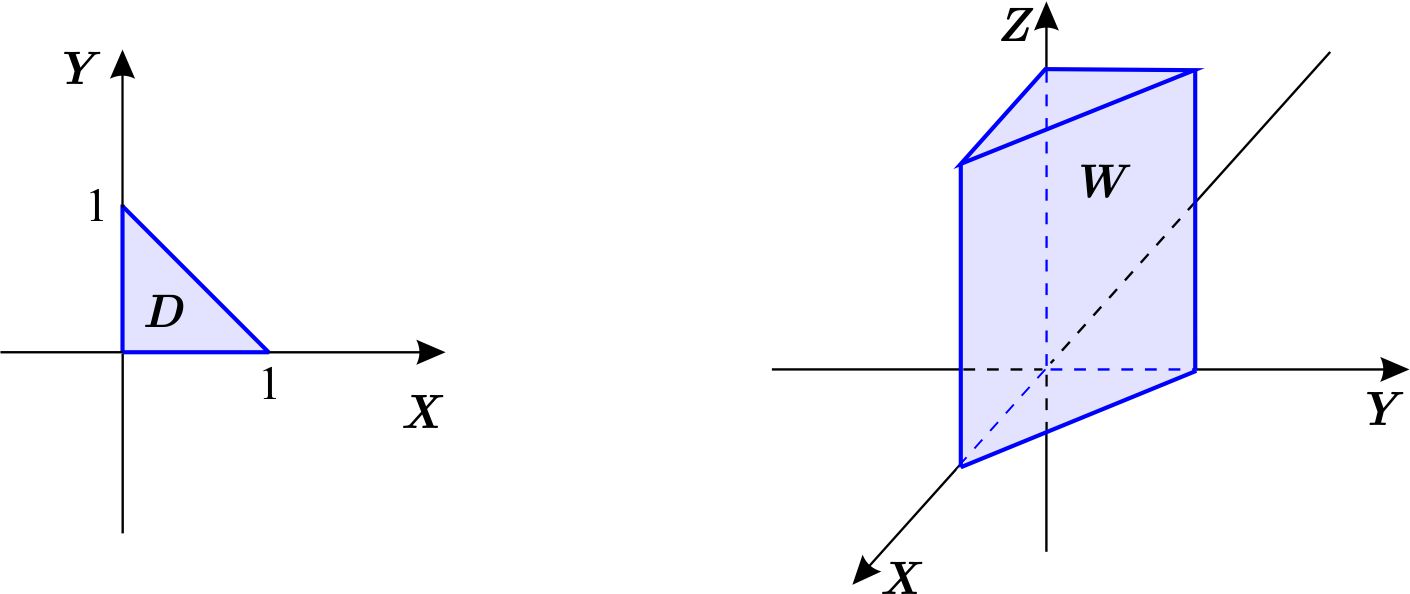
    La región \(W \) está limitada verticalmente por los planos \(YZ, \) \(XZ \) y \(x+y=1. \)

    Para escribir la integral en el orden \(dx\,dy\,dz, \) debemos escribir \(W \) como de tipo II. Usaremos la forma: \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,a\leq z\leq b,\quad \phi _{1}\left( z\right) \leq y\leq \phi _{2}\left( z\right) ,\quad \psi _{1}\left( z,y\right) \leq x\leq \psi _{2}\left( z,y\right) \right. \right\} , \end{equation*} observamos que las dos primeras condiciones, describen una región plana, escrita como de tipo \(2 \) en el plano \(YZ. \)

    Proyectamos \(W \) en el plano \(YZ \) :

     

     

     

     

     

     

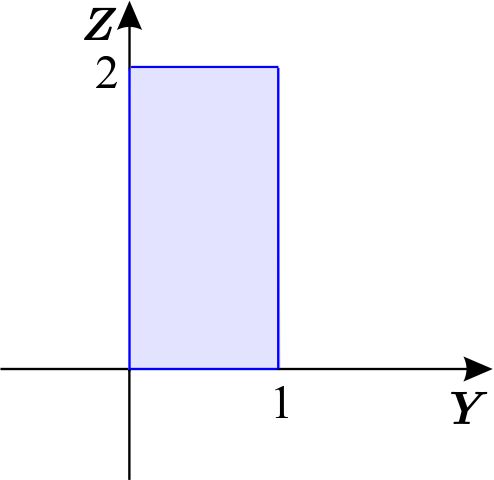
    de donde \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,0\leq z\leq 2,\quad 0\leq y\leq 1,\quad 0\leq x\leq 1-y\right. \right\} , \end{equation*} entonces \begin{equation*} \text{Vol}(W) = \int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2}dz\,dy \,dx=\int_{0}^{2}\int_{0}^{1}\int_{0}^{1-y}dx \,dy\,dz. \end{equation*} Podemos verificar directamente que las dos integrales anteriores son iguales: \begin{eqnarray*} \int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2}dz\,dy\,dx&=&\int_{0}^{1}\int_{0}^{1-x}2 dy\,dx \\ &=&\int_{0}^{1} 2(1-x) dx = 1 \\ \end{eqnarray*} \begin{eqnarray*} \int_{0}^{2}\int_{0}^{1}\int_{0}^{1-y}dx\,dy\,dz&=& \int_{0}^{2}\int_{0}^{1} 1-y \,dy\,dz \\ &=&\int_{0}^{2} \frac{1}{2} dz = 1 \end{eqnarray*}

  2. Considera la integral \[\int_{-4}^{4}\int_{-\sqrt{ 16-y^{2}}}^{\sqrt{16-y^{2}}}\int_{\sqrt{x^{2}+y^{2}} }^{4}dz\,dx\,dy. \] Dibuja la región \(W \) cuyo volumen corresponde a la integral dada y escribe la integral en el orden \(dy\,dx\,dz \) .

     

    Solución:

     

    La proyección en el plano \(XY \) es una región plana \(D \) de tipo \(2 \) : \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-4\leq y\leq 4,\quad -\sqrt{ 16-y^{2}}\leq x\leq \sqrt{16-y^{2}}\right. \right\} . \end{equation*} La región \(W \) está dada por \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\quad \sqrt{x^{2}+y^{2}}\leq z\leq 4\right. \right\} \\ W &=&\left\{ \left( x,y,z\right) \,\left\vert \,-4\leq y\leq 4,\quad -\sqrt{ 16-y^{2}}\leq x\leq \sqrt{16-y^{2}},\quad \sqrt{x^{2}+y^{2}}\leq z\leq 4\right. \right\} \end{eqnarray*}

     

     

     

     

     

     

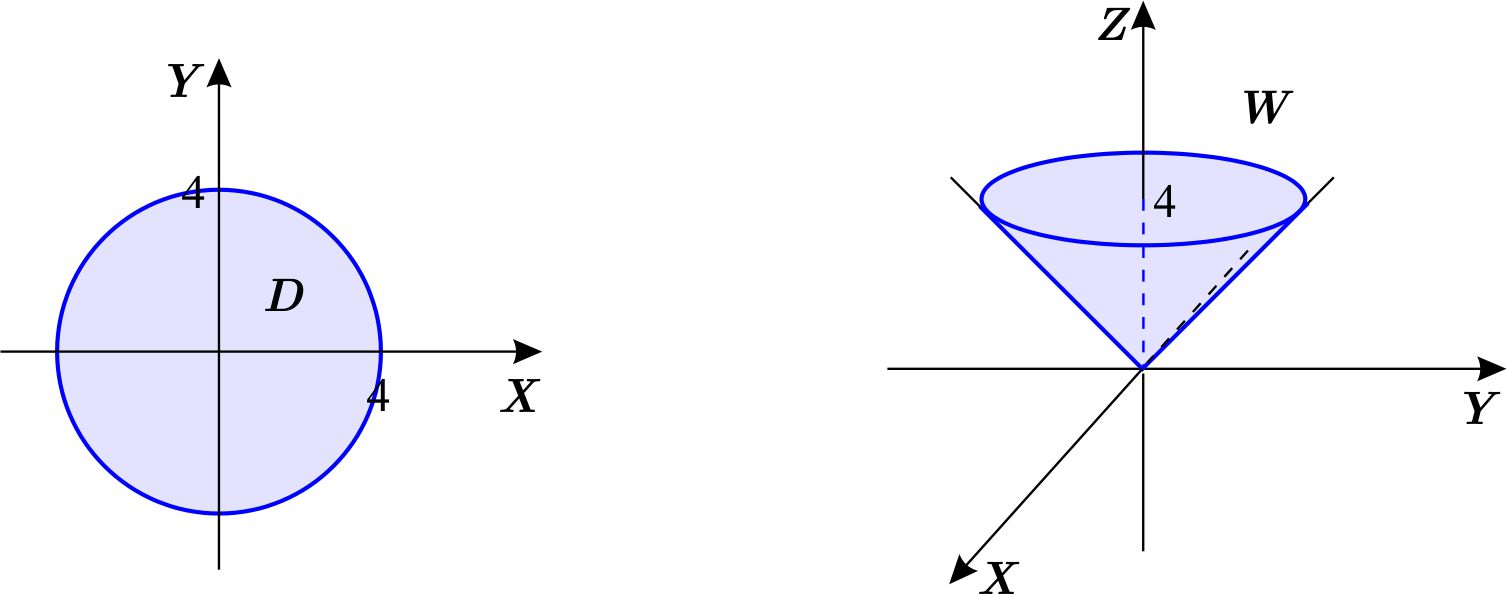
    Para escribir la integral en el orden \(dy\,dx\,dz, \) debemos escribir \(W \) como de tipo III. Usaremos la forma \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,c\leq z\leq d,\quad \phi _{1}\left( z\right) \leq x\leq \phi _{2}\left( z\right) ,\quad \psi _{1}\left( x,z\right) \leq y\leq \psi _{2}\left( x,z\right) \right. \right\} , \end{equation*} observamos que las dos primeras condiciones, describen una región en el plano \(XZ \) , escrita como de tipo \(2. \)

    Proyectamos \(W \) en el plano \(XZ \) :

     

     

     

     

     

     

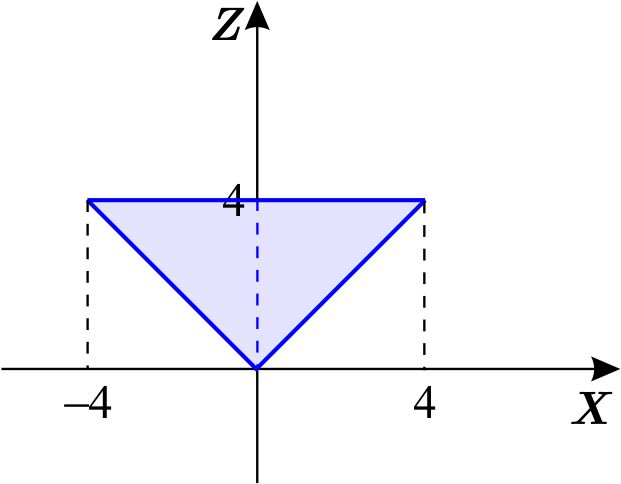
    de donde \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,0\leq z\leq 4,\quad -z\leq x\leq z,\quad -\sqrt{z^{2}-x^{2}}\leq y\leq \sqrt{z^{2}-x^{2}}\right. \right\} , \end{equation*} entonces \begin{equation*} \text{Vol}(W)=\int_{-4}^{4}\int_{-\sqrt{16-y^{2}}}^{\sqrt{16-y^{2}} }\int_{\sqrt{x^{2}+y^{2}}}^{4}dz\,dx\,dy=\int_{0}^{4} \int_{-z}^{z}\int_{-\sqrt{z^{2}-x^{2}}}^{\sqrt{ z^{2}-x^{2}}}dy\,dx\,dz. \end{equation*} Cualquiera de estas dos integrales es difícil de calcular. En la siguiente sección veremos que cuando la región de integración es un cono, la manera más fácil de calcularlas es utilizar coordenadas cilíndricas.

  3. Escribe la integral correspondiente al volumen de la región que se encuentra dentro del cilindro \(x^{2}+y^{2}=16 \) y la esfera \( x^{2}+y^{2}+z^{2}=25. \) Dibuja la región y escribe la integral, usando:
    1. El orden \(dz\,dy\,dx. \)
    2. El orden \(dx\,dz\,dy. \)

     

    Solución:

     

     

     

     

     

     

     

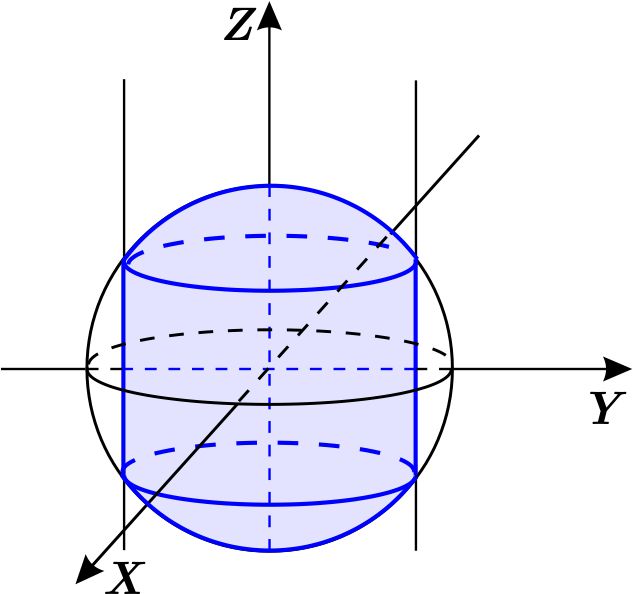
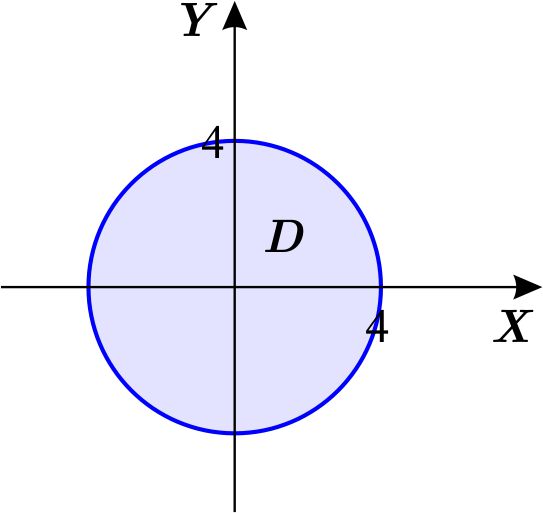
    1. Para escribir la integral usando el orden \(dz\,dy\,dx, \) debemos escribir la región \(W \) como de tipo I, observamos que su proyección en el plano \(XY \) es el círculo con centro en el origen y radio \(4 \) :

       

       

       

       

       

       

      que escribimos como una región de tipo \(1 \) en el plano \(XY \) para obtener el orden de integración \(dydx \) , es decir, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}}\right. \right\} . \end{equation*} La región \(W \) está dada por \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,y\right) \in D,\quad -\sqrt{25-x^{2}-y^{2}}\leq z\leq \sqrt{25-x^{2}-y^{2}}\right. \right\} \\ W &=&\left\{ \left( x,y,z\right) \,\left\vert -4\leq x\leq 4,\quad -\sqrt{ 16-x^{2}}\leq y\leq \sqrt{16-x^{2}},\quad -\sqrt{25-x^{2}-y^{2}}\leq z\leq \sqrt{25-x^{2}-y^{2}}\right. \right\} , \end{eqnarray*} entonces \begin{equation*} \text{Vol }W=\int_{-4}^{4}\int_{-\sqrt{16-x^{2}}}^{\sqrt{ 16-x^{2}}}\int_{-\sqrt{25-x^{2}-y^{2}}}^{\sqrt{25-x^{2}-y^{2}} }dz\,dydx. \end{equation*}

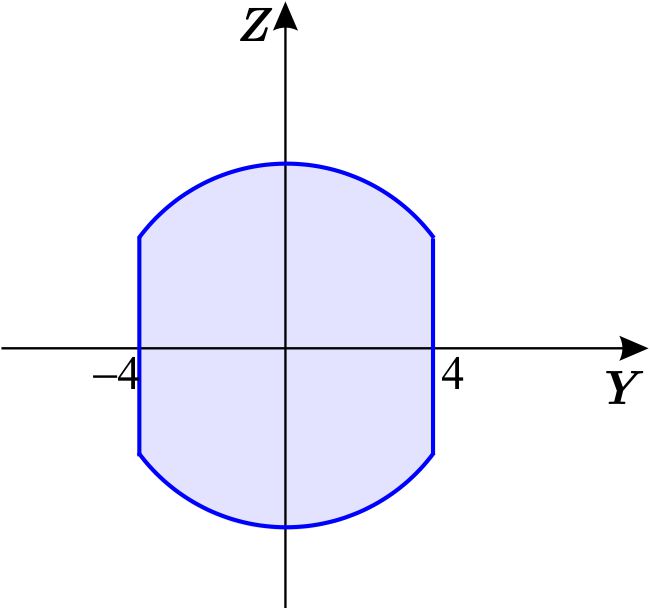
    2. Para escribir la integral usando el orden \(dx\,dz\,dy, \) debemos escribir la región \(W \) como de tipo II, observamos que su proyección en el plano \(YZ \) es:

       

       

       

       

       

       

      que escribimos como una región de tipo \(1 \) en el plano \(YZ \) , es decir, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-4\leq y\leq 4,\quad -\sqrt{ 25-y^{2}}\leq z\leq \sqrt{25-y^{2}}\right. \right\} . \end{equation*} La región \(W \) está dada por \begin{eqnarray*} W &=&\left\{ \left( x,y,z\right) \,\left\vert \,\left( y,z\right) \in D,\quad -\sqrt{16-y^{2}}\leq x\leq \sqrt{16-y^{2}}\right. \right\} \\ W &=&\left\{ \left( x,y,z\right) \,\left\vert -4\leq y\leq 4,\quad -\sqrt{ 25-y^{2}}\leq z\leq \sqrt{25-y^{2}},\quad -\sqrt{16-y^{2}}\leq x\leq \sqrt{ 16-y^{2}}\right. \right\} . \end{eqnarray*} Entonces \begin{equation*} \text{Vol }W=\int_{-4}^{4}\int_{-\sqrt{25-y^{2}}}^{\sqrt{ 25-y^{2}}}\int_{-\sqrt{16-y^{2}}}^{\sqrt{16-y^{2}}}dx\,dz\,dy. \end{equation*}

    Cualquiera de las integrales de los incisos (a) o (b) es difícil de calcular. En la siguiente sección veremos que cuando la región de integración parte de una esfera o de un cilindro, la manera más fácil de calcularlas es utilizar coordenadas esféricas o cilíndricas.
  4. Considera la región \(W \) que se encuentra dentro del cilindro \( x^{2}+y^{2}=9, \) acotada por los planos \(z=0 \) y \(x+y+z-4=0. \) Dibuja la región y escribe la integral que determina el volumen de \(W \) , usando:
    1. El orden \(dz\,dx\,dy. \)
    2. El orden \(dx\,dz\,dy. \)

     

    Solución:

     

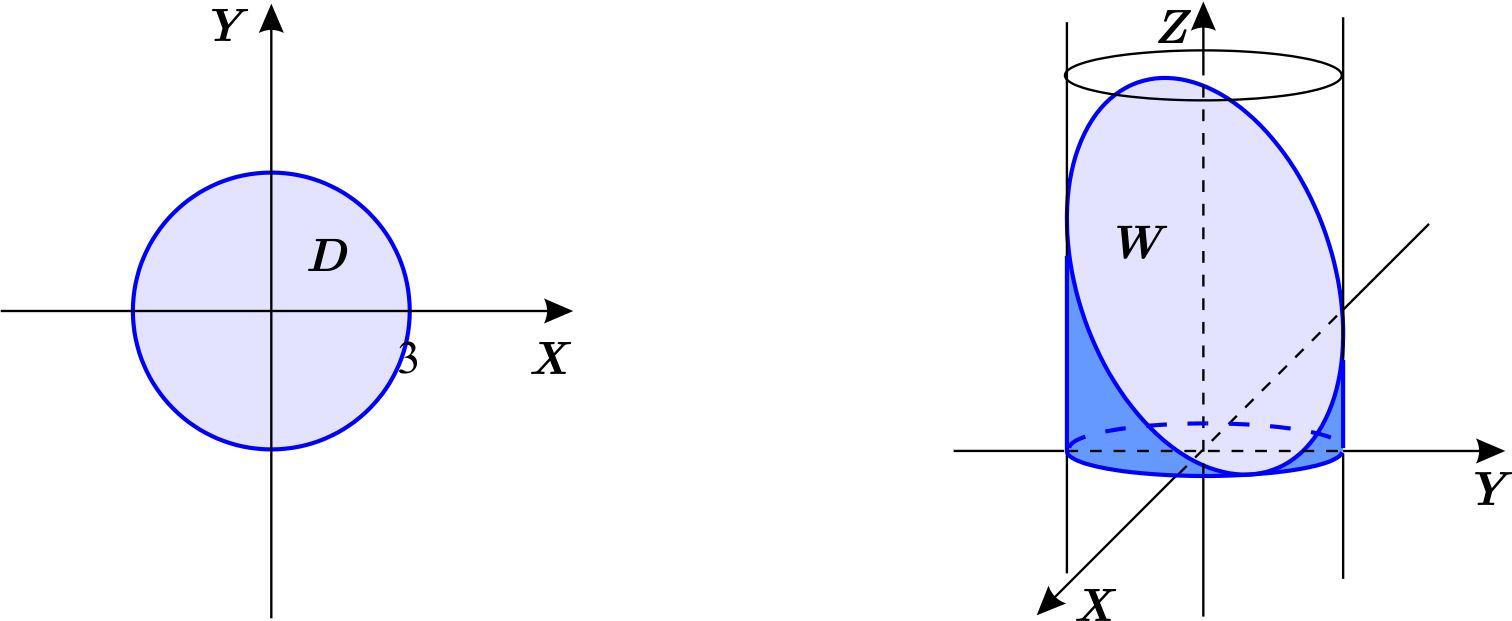
    1. Dibujamos la región y consideramos su proyección en el plano \(XY. \)

       

       

       

       

       

       

      Para establecer el orden \(dzdxdy, \) debemos escribir la región \(D \) de tipo \(2 \) , es decir, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,-3\leq y\leq 3,\;\;-\sqrt{9-y^{2}} \leq x\leq \sqrt{9-y^{2}}\right. \right\} , \end{equation*} de donde \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert -3\leq y\leq 3,\;\;-\sqrt{9-y^{2}} \leq x\leq \sqrt{9-y^{2}},\;\;0\leq z\leq 4-x-y\right. \right\} . \end{equation*} Entonces \begin{equation*} \text{Vol }W=\int_{-3}^{3}\int_{-\sqrt{9-y^{2}}}^{\sqrt{ 9-y^{2}}}\int_{0}^{4-x-y}dz\,dx\,dy \end{equation*}

    2. Para establecer el orden \(dx\,dz\,dy, \) debemos considerar la proyección de la región \(W \) en el plano \(YZ \) , si llamamos \(D_{1} \) a dicha proyección, ésta debe ser escrita como de tipo \(1 \) en el plano \( XY \) .

      Para ver la proyección, observamos que si \(x=0, \) sustituyendo en la ecuación del cilindro, obtenemos \begin{eqnarray*} x^{2}+y^{2} &=&9 \\ y^{2} &=&9 \\ y &=&\pm 3 \end{eqnarray*} y al sustituir en la ecuación del plano: \begin{eqnarray*} x+y+z-4 &=&0 \\ y+z-4 &=&0 \\ z &=&4-y, \end{eqnarray*} que es la recta en el plano \(YZ \) con pendiente \(-1, \) que pasa por los puntos \( \left( -3,7\right) \) y \(\left( 3,1\right) . \) Como la región \(D_{1} \) se encuentra sobre el plano \(YZ, \) tenemos

       

       

       

       

       

       

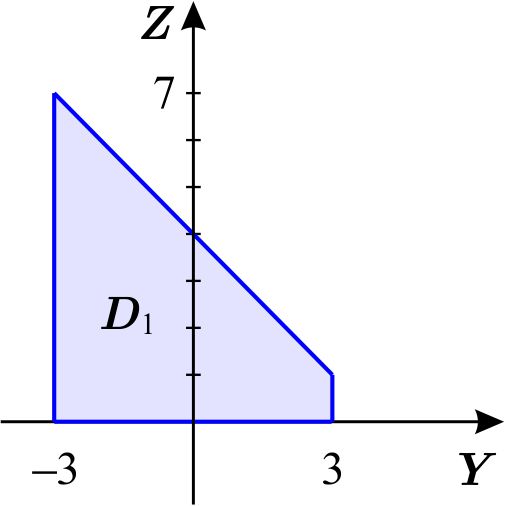
      de donde \begin{equation*} D_{1}=\left\{ \left( y,z\right) \,\left\vert \,-3\leq y\leq 3,\;\;0\leq z\leq 4-y\right. \right\} , \end{equation*} entonces \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert -3\leq y\leq 3,\;\;0\leq z\leq 4-y,\;\;-\sqrt{9-y^{2}}\leq x\leq \sqrt{9-y^{2}}\right. \right\} . \end{equation*} Así \begin{equation*} \text{Vol }W=\int_{-3}^{3}\int_{0}^{4-y}\int_{- \sqrt{9-y^{2}}}^{\sqrt{9-y^{2}}}dx\,dz\,dy. \end{equation*}

    Cualquiera de las integrales de los incisos (a) o (b) es difícil de calcular. En la siguiente sección veremos que cuando la región de integración es parte de un cilindro, la manera más fácil de calcularlas es utilizar coordenadas cilíndricas.
  5. Considera la región \(W \) que se encuentra dentro del cono \( 4x^{2}+z^{2}=y^{2}, \) acotada por el plano \(y=9 \) y debajo del plano \(z=0. \) Dibuja la región y escribe la integral que determina el volumen de \(W \) , usando:
    1. El orden \(dz\,dx\,dy. \)
    2. El orden \(dx\,dz\,dy. \)

     

    Solución:

     

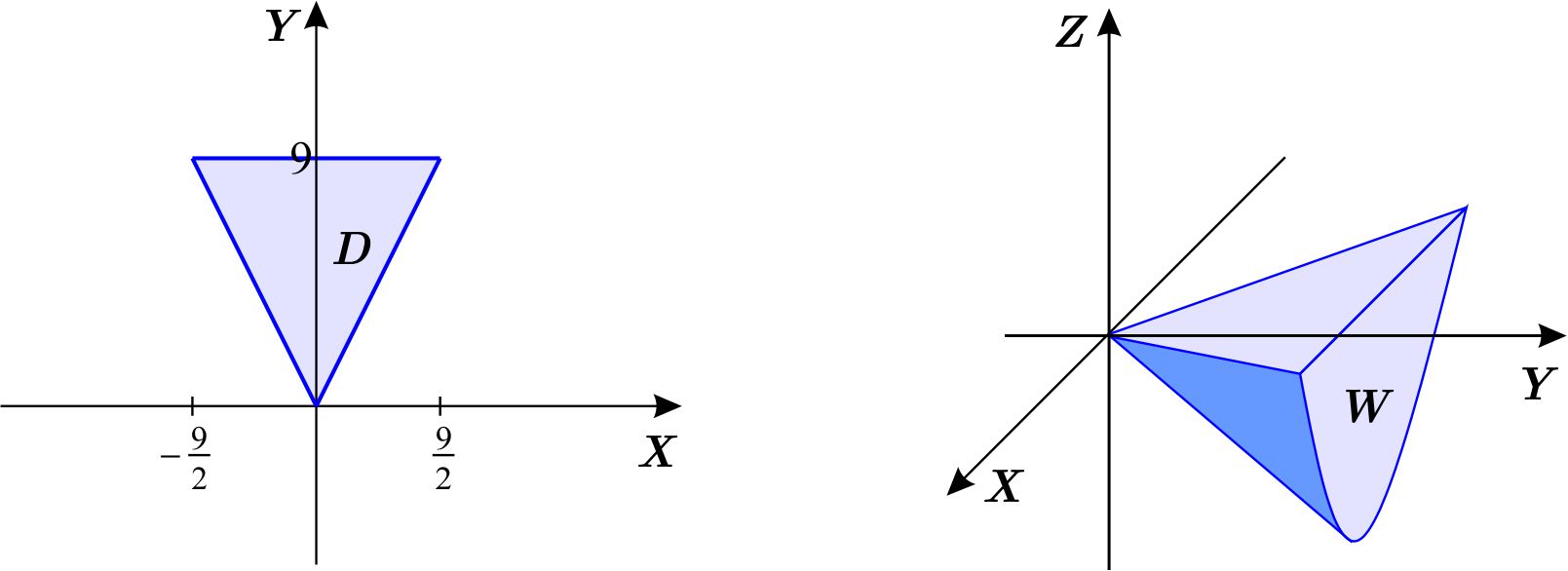
    1. Dibujamos la región y consideramos su proyección en el plano \(XY. \)

       

       

       

       

       

       

      Para ver la proyección en el plano \(XY, \) consideramos \(z=0 \) en la ecuación del cono: \begin{eqnarray*} 4x^{2}+z^{2} &=&y^{2} \\ 4x^{2} &=&y^{2} \\ y &=&\left\vert 2x\right\vert , \end{eqnarray*} puesto que \(0\leq y\leq 9, \) obtenemos la figura de la izquierda.

      Para establecer el orden \(dz\,dx\,dy, \) debemos escribir la región \(D \) de tipo \(2 \) , es decir, \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,0\leq y\leq 9,\;\;-\dfrac{y}{2} \leq x\leq \dfrac{y}{2}\right. \right\} \end{equation*} de donde \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,0\leq y\leq 9,\;\;-\dfrac{y}{2} \leq x\leq \dfrac{y}{2},\;\;-\sqrt{y^{2}-4x^{2}}\leq z\leq 0\right. \right\} . \end{equation*} Entonces \begin{equation*} \text{Vol }W=\int_{0}^{9}\int_{-\frac{y}{2}}^{\frac{y}{2} }\int_{-\sqrt{y^{2}-4x^{2}}}^{0}dz\,dx\,dy. \end{equation*}

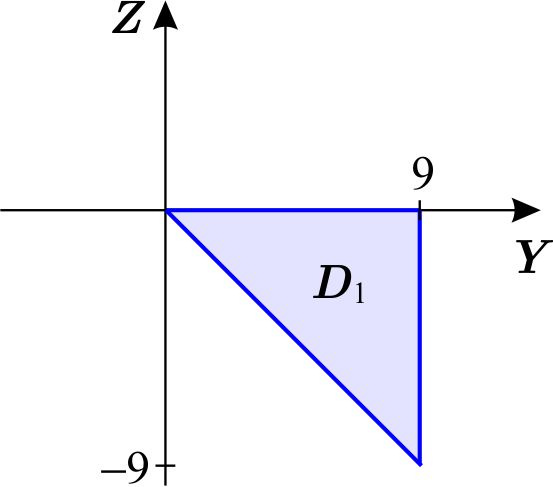
    2. Para establecer el orden \(dx\,dz\,dy, \) debemos considerar la proyección de la región \(W \) en el plano \(YZ \) , si llamamos \(D_{1} \) a dicha proyección, ésta debe ser escrita como de tipo \(1 \) en el plano \( XY \) . Para ver la proyección, observamos que si \(x=0, \) sustituyendo en la ecuación del cilindro, obtenemos \begin{eqnarray*} 4x^{2}+z^{2} &=&y^{2} \\ z^{2} &=&y^{2} \\ z &=&\left\vert y\right\vert \end{eqnarray*} y puesto que \(\,0\leq y\leq 9, \) \(z\leq 0, \) tenemos

       

       

       

       

       

       

      de donde \begin{equation*} D_{1}=\left\{ \left( y,z\right) \,\left\vert \,0\leq y\leq 9,\;\;-y\leq z\leq 0\right. \right\} , \end{equation*} entonces \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert 0\leq y\leq 9,\;\;-y\leq z\leq 0,\;\;-\dfrac{\sqrt{y^{2}-z^{2}}}{2}\leq x\leq \dfrac{\sqrt{y^{2}-z^{2}}}{2} \right. \right\} . \end{equation*} Así \begin{equation*} \text{Vol }W=\int_{0}^{9}\int_{-y}^{0}\int_{- \frac{\sqrt{y^{2}-z^{2}}}{2}}^{\frac{\sqrt{y^{2}-z^{2}}}{2}}dx\,dz\,dy. \end{equation*}

Cualquiera de las integrales de los incisos (a) o (b) es difícil de calcular. En la siguiente sección veremos que cuando la región de integración es parte de un cono, la manera más fácil de calcularlas es utilizar coordenadas cilíndricas.

Ejercicios

  1. Considera la integral \[\int_{1}^{2}\int_{1}^{z} \int_{0}^{2}dx\,dy\,dz. \] Dibuja la región \(W \) cuyo volumen corresponde a la integral dada y escribe la integral en el orden \(dy\,dz\,dx \).

  2. Escribe la integral correspondiente al volumen de la región que se encuentra dentro de la esfera \(x^{2}+y^{2}+z^{2}=9 \) y bajo el plano \(z=-1. \) Dibuja la región y escribe la integral, usando:
    1. El orden \(dz\,dy\,dx. \)
    2. El orden \(dx\,dy\,dz. \)


  3. La región \(W \) está dada como \begin{equation*} W=\left\{ \left( x,y,z\right) \,\left\vert \,\left( x,z\right) \in D,\quad 0\leq y\leq 2\right. \right\} \end{equation*} donde \(D \) es la región encerrada por las rectas \(z=x, \) \(z=-x+4, \) \(z=1. \) Escribe la integral que determina el volumen de \(W \) :
    1. Usando el orden \(dy\,dz\,dx. \)
    2. Usando el orden \(dy\,dx\,dz. \)
    3. Dibuja la proyección de \(W \) en el plano \(XY \) y escribe la integral en el orden \(dz\,dy\,dx. \)
    Universidad Nacional Autónoma de México