
Integrales Dobles
Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

 |
Integrales DoblesAngel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) |  |
Solución:
La región \( D \) en el plano \(XY\) sobre la que hay que integrar es
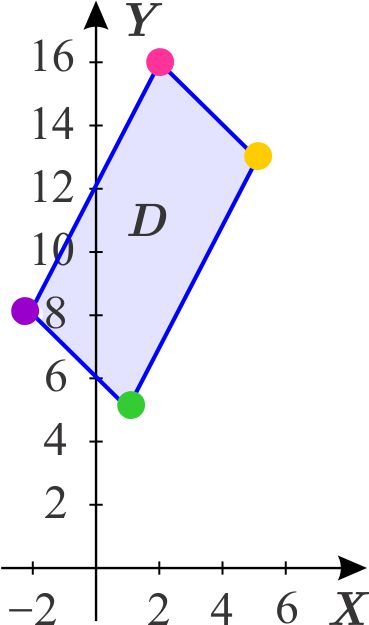
El cambio de variables propuesto corresponde a la transformación lineal \( L:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2} \), definida como \(L\left( \left( u,v\right) \right) =\left( u-v,v+2u\right) \), por lo que su matriz asociada es \begin{equation*} \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right) . \end{equation*} O sea, \begin{equation*} \ L\left( u,v\right) =\left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right) \left( \begin{array}{c} u \\ v \end{array} \right) \end{equation*} Puesto que la transformación es lineal y por tanto, transforma paralelogramos en paralelogramos, para determinar de qué paralelogramo \( D_{1}\) del plano \(UV\) proviene el paralelogramo \(D,\) basta que conozcamos de qué puntos provienen sus vértices.
Para esto consideramos la transformación inversa \(L^{-1} \), cuya matriz asociada es la inversa de la de \(L \)
Así, \begin{equation*} L^{-1}\left( x,y\right) =\left( \begin{array}{cc} \dfrac{1}{3} & \dfrac{1}{3} \\ -\dfrac{2}{3} & \dfrac{1}{3} \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) , \end{equation*} es decir, \begin{equation*} L^{-1}\left( x,y\right) =\left( \dfrac{1}{3}x+\dfrac{1}{3}y,-\dfrac{2}{3}x+ \dfrac{1}{3}y\right) , \end{equation*} o sea \begin{eqnarray*} u &=&\dfrac{1}{3}x+\dfrac{1}{3}y \\ v &=&-\dfrac{2}{3}x+\dfrac{1}{3}y, \end{eqnarray*} de donde: \begin{eqnarray*} \ L^{-1}\left( 1,5\right) &=&\left( \dfrac{1}{3}+\dfrac{5}{3},-\dfrac{2}{3}+ \dfrac{5}{3}\right) =\left( 2,1\right) \\ L^{-1}\left( 5,13\right) &=&\left( \dfrac{5}{3}+\dfrac{13}{3},-\dfrac{10}{3}+ \dfrac{13}{3}\right) =\left( 6,1\right) \\ L^{-1}\left( 2,16\right) &=&\left( \dfrac{2}{3}+\dfrac{16}{3},-\dfrac{4}{3}+ \dfrac{16}{3}\right) =\left( 6,4\right) \\ L^{-1}\left( -2,8\right) &=&\left( -\dfrac{2}{3}+\dfrac{8}{3},\dfrac{4}{3}+ \dfrac{8}{3}\right) =\left( 2,4\right) . \end{eqnarray*} Entonces \(D\) proviene del rectángulo \(D_{1}\) que tiene estos vértices y que se indica en la figura siguiente
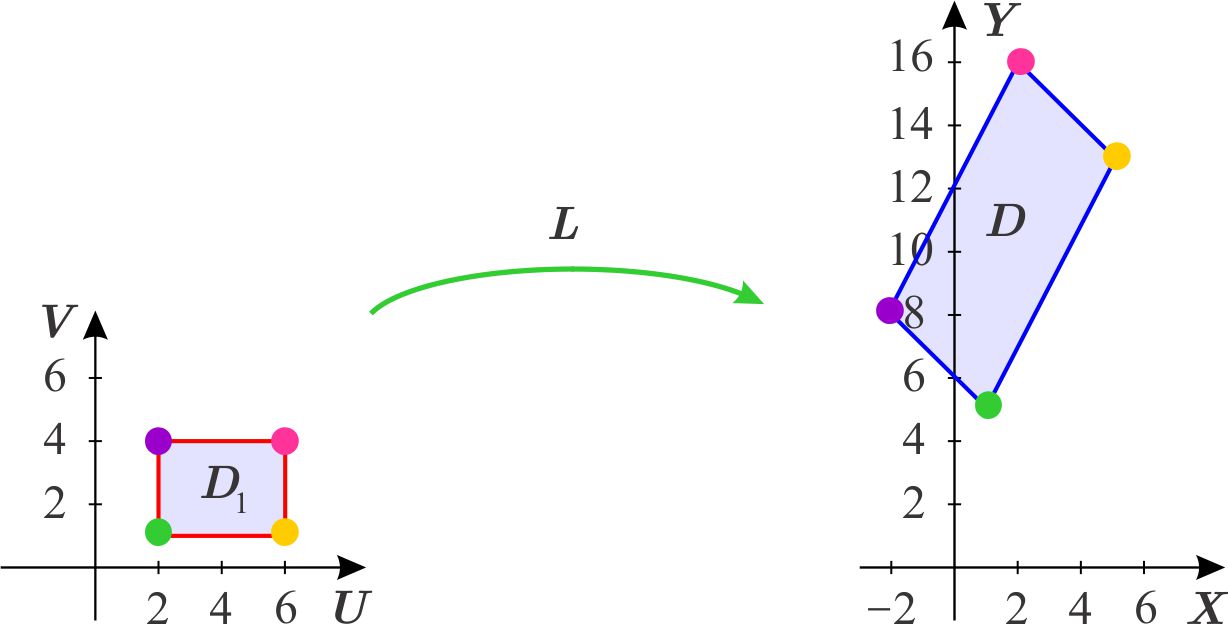
Para calcular la integral, necesitamos el jacobiano de la transformación \(L \): \begin{eqnarray*} \dfrac{\partial \left( x,y\right) }{\partial \left( u,v\right) } &=&\det \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right) \\ &=&3. \end{eqnarray*} Entonces \begin{eqnarray*} \iint_{D}xy\,dx\,dy &=&\iint_{D_{1}}\left( f\circ T\right) \left( u,v\right) \left\vert \dfrac{\partial \left( x,y\right) }{ \partial \left( u,v\right) }\right\vert \,du\,dv \\ &=&\int_{1}^{4}\int_{2}^{6}\left( u-v\right) \left( v+2u\right) \left( 3\right) \,du\,dv \\ &=&3\int_{1}^{4}\int_{2}^{6}2u^{2}-vu-v^{2}\,du\,dv \\ &=&3\int_{1}^{4}\left. \dfrac{2}{3}u^{3}-\dfrac{1}{2} vu^{2}-v^{2}u\right\vert _{2}^{6}\,dv \\ &=&3\int_{1}^{4}\dfrac{2}{3}\left( 6^{3}\right) -\dfrac{1}{2} v\left( 6^{2}\right) -v^{2}\left( 6\right) -\left( \dfrac{2}{3}\left( 2^{3}\right) -\dfrac{1}{2}v\left( 2^{2}\right) -v^{2}\left( 2\right) \right) \,dv \\ &=&3\int_{1}^{4}\dfrac{2}{3}\left( 6^{3}-2^{3}\right) -\dfrac{1}{2} v\left( 6^{2}-2^{2}\right) -v^{2}\left( 6-2\right) \,dv \\ &=&3\left. \left( \dfrac{2}{3}\left( 6^{3}-2^{3}\right) v-\dfrac{16}{2}v^{2}- \dfrac{4}{3}v^{3}\right) \right\vert _{1}^{4} \\ &=&3\left( \left( \dfrac{416}{3}\left( 4\right) -8\left( 4^{2}\right) - \dfrac{4}{3}\left( 4^{3}\right) \right) -\left( \left( \dfrac{416}{3}-8- \dfrac{4}{3}\right) \right) \right) \\ &=&3\left( \dfrac{416}{3}\left( 4-1\right) -8\left( 16-1\right) -\dfrac{4}{3} \left( 4^{3}-1\right) \right) \\ &=&3\left( 416-120-84\right) \\ &=&636. \end{eqnarray*}
Ejemplos
Solución:
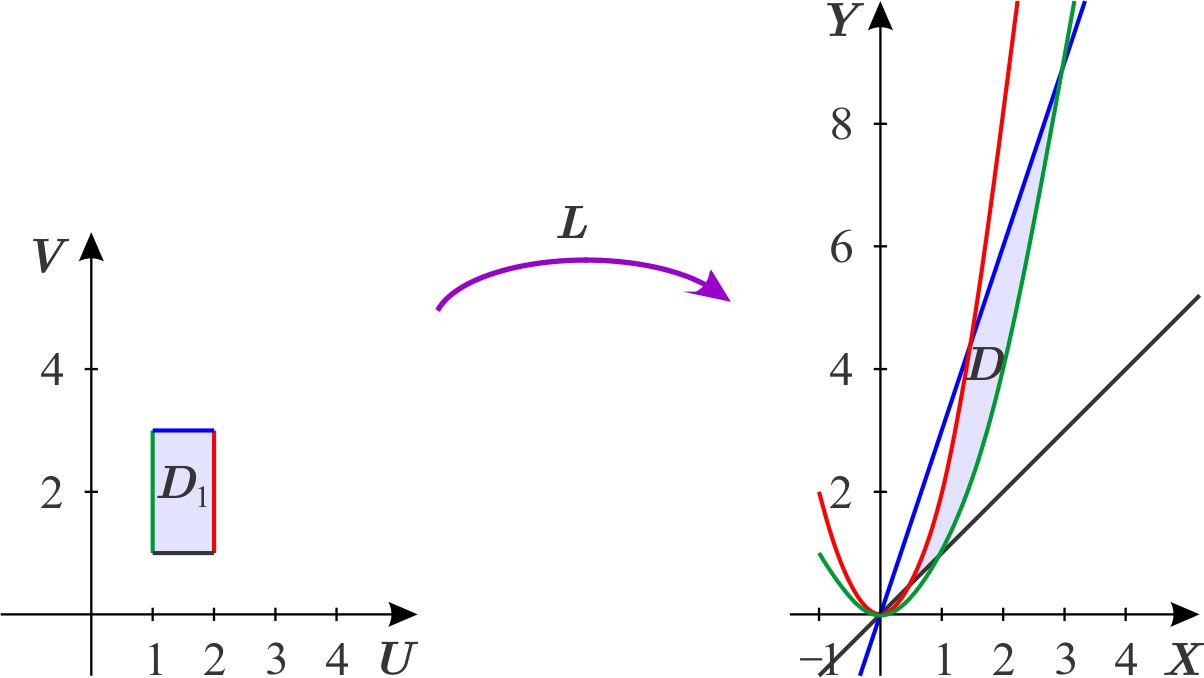
La región es:

Llamamos \(L\) a la transformación del plano \(UV\) al plano \(XY, \) la cual es tal que su inversa está definida en \(D\subset \left\{ \left. \left( x,y\right) \in \mathbb{R}^{2}\right\vert x\neq 0\text{ y }y\neq 0\right\} \) como \begin{equation*} L^{-1}\left( x,y\right) =\left( \dfrac{y}{x^{2}},\dfrac{y}{x}\right) =\left( u,v\right) \end{equation*} Para encontrar la región en el plano \(UV\) la cual tiene como imagen la región \(D\) aplicamos \(L^{-1}\) a la frontera de la región \(D \):
La recta \(y=x\) es la imagen bajo \(L\) de la recta \(v=1 \), ya que las siguientes ecuaciones son equivalentes \begin{eqnarray*} y &=&x \\ \dfrac{y}{x} &=&1 \\ v &=&1. \end{eqnarray*} La recta \(y=3x\) es la imagen bajo \(L\) de la recta \(v=3 \), ya que las siguientes ecuaciones son equivalentes \begin{eqnarray*} y &=&3x \\ \dfrac{y}{x} &=&3 \\ v &=&3. \end{eqnarray*} La parábola \(y=x^{2}\) es la imagen bajo \(L\) de la recta \(u=1 \), ya que las siguientes ecuaciones son equivalentes \begin{eqnarray*} y &=&x^{2} \\ \dfrac{y}{x^{2}} &=&1 \\ u &=&1. \end{eqnarray*} La parábola \(y=2x^{2}\) es la imagen bajo \(L\) de la recta \(u=2 \), ya que las siguientes ecuaciones son equivalentes \begin{eqnarray*} y &=&2x^{2} \\ \dfrac{y}{x^{2}} &=&2 \\ u &=&2. \end{eqnarray*} Es decir, \(D\) proviene del rectángulo \(D_{1}\) en el plano \(UV\) que está limitado por las rectas \(v=1,v=3,u=1\) y \(u=2.\)
Para calcular la integral debemos encontrar el jacobiano de la transformación \(L,\) inversa de \(L^{-1} \). La regla de correspondencia de \(L:D\subset \left\{ \left. \left( x,y\right) \in \mathbb{R}^{2}\right\vert x\neq 0\text{ y }y\neq 0\right\} \longrightarrow D_{1}\) es: \begin{eqnarray*} u &=&\dfrac{y}{x^{2}} \\ v &=&\dfrac{y}{x}. \end{eqnarray*} Despejamos \(y\) de ambas ecuaciones: \begin{eqnarray} x^{2}u &=&y \notag \\ xv &=&y, \label{1} \tag{1} \end{eqnarray} de donde, \begin{equation*} x^{2}u=xv. \end{equation*} Como todo punto de \(D\) tiene abscisa \(x\neq 0,\) entonces \begin{equation*} x=\dfrac{v}{u}. \end{equation*} Sustituimos \(x=\dfrac{v}{u}\) en (\ref{1}): \begin{eqnarray*} \left( \dfrac{v}{u}\right) v &=&y \\ \dfrac{v^{2}}{u} &=&y, \end{eqnarray*} de donde, \begin{equation*} x=\dfrac{v}{u}\quad \quad \text{y} \quad \quad y=\dfrac{v^{2}}{u}. \end{equation*} Calculamos el jacobiano de la transformación \(L \) \begin{eqnarray*} \dfrac{\partial \left( x,y\right) }{\partial \left( u,v\right) } &=&\det \left( \begin{array}{cc} -\dfrac{v}{u^{2}} & \dfrac{1}{u} \\ -\dfrac{v^{2}}{u^{2}} & \dfrac{2v}{u} \end{array} \right) \\ &=&-\dfrac{2v^{2}}{u^{3}}+\dfrac{v^{2}}{u^{3}} \\ &=&-\dfrac{v^{2}}{u^{3}}. \end{eqnarray*} Calculamos la integral, \begin{eqnarray*} \iint_{D}xy\,dx\,dy &=&\int_{1}^{3}\int_{1}^{2}\left( \dfrac{v}{u}\right) \left( \dfrac{v^{2}}{u}\right) \left( \dfrac{v^{2}}{u^{3}}\right) \,du\,dv \\ &=&\int_{1}^{3}\int_{1}^{2}\dfrac{v^{5}}{u^{5}}\,du\,dv \\ &=&\int_{1}^{3}\left. -\dfrac{v^{5}}{4u^{5}}\right\vert _{1}^{2}\,dv \\ &=&\int_{1}^{3}-\dfrac{v^{5}}{64}-\left( -\dfrac{v^{5}}{4}\right) \,dv \\ &=&\int_{1}^{3}\dfrac{15}{64}v^{5}\,dv \\ &=&\dfrac{15}{64}\left( \left. \dfrac{v^{6}}{6}\right\vert _{1}^{3}\right) \\ &=&\dfrac{15}{64}\left( \dfrac{3^{6}}{6}-\dfrac{1}{6}\right) \\ &=&\dfrac{15}{64}\left( \dfrac{364}{3}\right) \\ &=&\dfrac{455}{16}. \end{eqnarray*}
Solución:
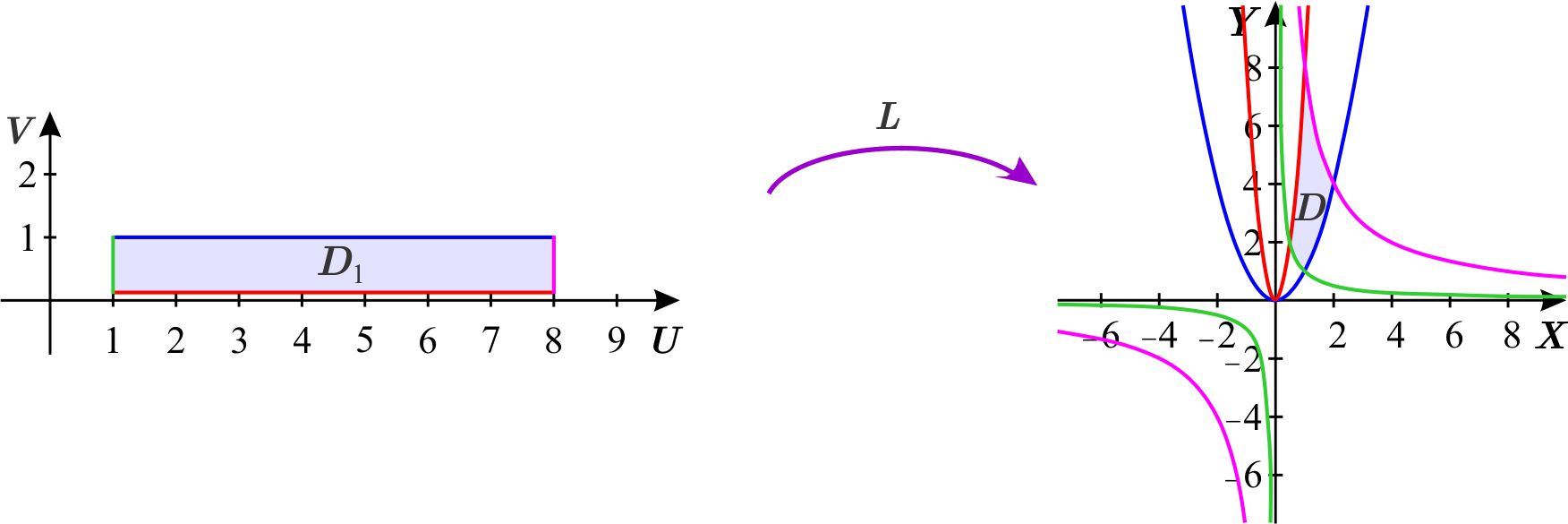
La región es:
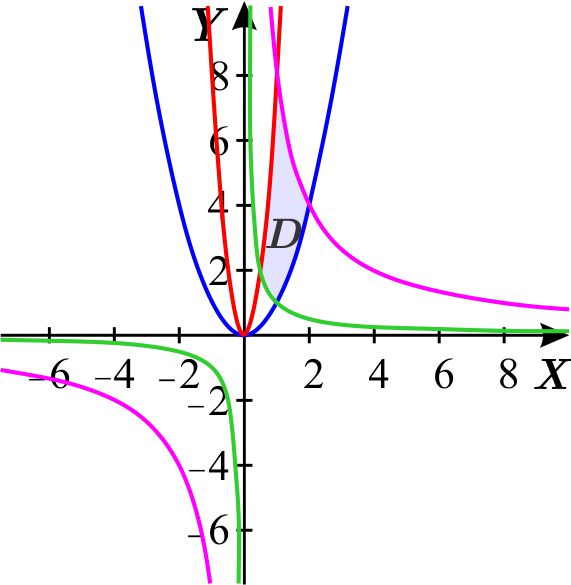
Determinemos la transformación \(L\) que da el cambio de variables propuesto. Como \begin{equation} xy=u\quad \quad \quad \text{y} \quad \quad \quad x^{2}=vy, \label{2}\tag{2} \end{equation} entonces \begin{equation} y=\frac{u}{x}\quad \quad \quad \text{y} \quad \quad \quad y=\frac{x^{2}}{v}, \label{3}\tag{3} \end{equation} de donde, \begin{eqnarray*} \frac{u}{x} &=&\frac{x^{2}}{v}; \\ uv &=&x^{3}; \\ x &=&\left( uv\right) ^{\frac{1}{3}}. \end{eqnarray*} De la primera igualdad en (\ref{3}) y esto último se sigue \begin{eqnarray*} y^{3} &=&\frac{u^{3}}{x^{3}}=\frac{u^{2}}{v}; \\ y &=&\left( \frac{u^{2}}{v}\right) ^{\frac{1}{3}}. \end{eqnarray*} Entonces \(L\left( u,v\right) =\left( \left( uv\right) ^{\frac{1}{3}},\left( \dfrac{u^{2}}{v}\right) ^{\frac{1}{3}}\right) \) está definida en el plano \(UV \), excepto en el eje \(U \).
Para encontrar la región \(D_{1}\) en el plano \(UV\) la cual tiene como imagen la región \(D\) encontramos de dónde proviene la frontera de la región \(D \).
La parábola \(y=x^{2}\) es la imagen bajo \(L\) de la recta \(v=1 \), ya que por (\ref{2}) las siguientes ecuaciones son equivalentes para \( y\neq 0 \) \begin{eqnarray*} y &=&x^{2}=vy \\ v &=&1. \end{eqnarray*} La parábola \(y=8x^{2}\) es la imagen bajo \(L\) de la recta \(v=\dfrac{1}{8} \), ya que por (\ref{2}) las siguientes ecuaciones son equivalentes para \(y\neq 0 \) \begin{eqnarray*} y &=&8x^{2} \\ y &=&8vy \\ v &=&\frac{1}{8}. \end{eqnarray*} La hipérbola \(y=\dfrac{1}{x}\) es la imagen bajo \(L\) de la recta \(u=1 \), ya que por (\ref{2}) las siguientes ecuaciones son equivalentes para \(x\neq 0 \) \begin{eqnarray*} y &=&\frac{1}{x} \\ yx &=&1 \\ u &=&1. \end{eqnarray*} La hipérbola \(y=\dfrac{8}{x}\) es la imagen bajo \(L\) de la recta \(u=8 \), ya que por (\ref{2}) las siguientes ecuaciones son equivalentes para \(x\neq 0 \) \begin{eqnarray*} y &=&\frac{8}{x}; \\ xy &=&8 \\ u &=&8. \end{eqnarray*} Es decir, \(D\) proviene del rectángulo \(D_{1}\) en el plano \(UV\) que está limitado por las rectas \(v=1,v=\dfrac{1}{8},u=1\) y \(u=8.\)
Para calcular el área de la región \(D\) encontraremos la integral \( \iint_{D}dx\,dy \), mediante el cambio de variables definido por \(L \). Para esto debemos encontrar el jacobiano de la transformación \(L. \) \begin{eqnarray*} \dfrac{\partial \left( x,y\right) }{\partial \left( u,v\right) } &=&\det \left( \begin{array}{cc} \dfrac{1}{3}\dfrac{v}{\left( uv\right) ^{\frac{2}{3}}} & \dfrac{1}{3}\dfrac{u }{\left( uv\right) ^{\frac{2}{3}}} \\ \dfrac{1}{3}\dfrac{2u}{v\left( \frac{u^{2}}{v}\right) ^{\frac{2}{3}}} & - \dfrac{1}{3}\dfrac{u^{2}}{v^{2}\left( \frac{u^{2}}{v}\right) ^{\frac{2}{3}}} \end{array} \right) \\ &=&-\frac{1}{3v}. \end{eqnarray*} Calculamos el área de la región \(D\) \begin{eqnarray*} \iint_{D}dx\,dy &=&\iint_{D_{1}}\left\vert \dfrac{\partial \left( x,y\right) }{\partial \left( u,v\right) }\right\vert \,du\,dv=\int_{\frac{1}{8}}^{1}\int_{1}^{8}\frac{1}{3v} \,du\,dv \\ &=&\frac{7}{3}\int_{\frac{1}{8}}^{1}\dfrac{1}{v}\,dv \\ &=&\frac{7}{3}\left( \log \left( 1\right) -\log \left( \frac{1}{8}\right) \right) \\ &=&\frac{7}{3}\log \left( 8\right) \\ &=&7\log \left( 2\right) . \end{eqnarray*}