Integrales Dobles Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Cambio en el Orden de Integración

Ejemplos

1. Calcular \(\iint_{D}xy\,dx\,dy\) donde \(D\) es el triángulo con vértices \(\left( -3,1\right) , \) \(\left( 2,-5\right) \) y \(\left( 6,1\right) . \)

    

   Solución:

   Dibujamos la región \(D.\)

    

   

    

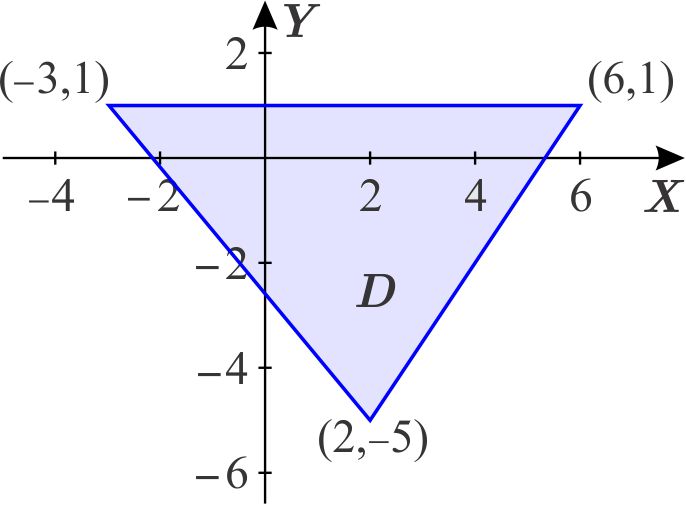
   Determinamos las ecuaciones de los lados que unen \(\left( -3,1\right) \) con \( \left( 2,-5\right) \) y \(\left( 2,-5\right) \) con \(\left( 6,1\right) . \)

   • Ecuación del lado que une \(\left( -3,1\right) \) con \(\left( 2,-5\right) \) \begin{equation*} y=-\dfrac{6}{5}x-\dfrac{13}{5}, \end{equation*} o bien \begin{equation*} x=-\dfrac{5}{6}y-\dfrac{13}{6}. \end{equation*}
   • Ecuación del lado que une \(\left( 2,-5\right) \) con \(\left( 6,1\right) . \) \begin{equation*} y=\dfrac{3}{2}x-8, \end{equation*} o bien, \begin{equation*} x=\dfrac{2}{3}y+\dfrac{16}{3}. \end{equation*}
   Observamos que si consideramos la región \(D\) como de tipo 1, hay que considerar una función combinada y a fin de cuentas tendremos que presentarla como la unión de dos regiones del tipo 1, pero si la consideramos de tipo 2 tenemos \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ -5,1\right] ,\quad \quad -\dfrac{5}{6}y-\dfrac{13}{6}\leq x\leq \dfrac{2}{3}y+\dfrac{16}{3} \right. \right\} \end{equation*} y la integral a calcular es \begin{equation} \iint_{D}xy\,dx\,dy=\int_{-5}^{1}\int_{-\frac{5 }{6}y-\frac{13}{6}}^{\frac{2}{3}y+\frac{16}{3}}xy\,dx\,dy.\, \label{1} \tag{1} \end{equation} Si pensamos la región \(D\) como de tipo 1, entonces: \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{equation*} D_{1}=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ -3,2\right] ,\quad \quad -\dfrac{6}{5}x-\dfrac{13}{5}\leq y\leq 1\right. \right\} \end{equation*} y \begin{equation*} D_{2}=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 2,6\right] ,\quad \quad \dfrac{3}{2}x-8\leq y\leq 1\right. \right\} . \end{equation*} Entonces la integral a calcular es \begin{equation*} \iint_{D}xy\,dx\,dy=\int_{-3}^{2}\int_{-\frac{6 }{5}x-\frac{13}{5}}^{1}xy\,dy\,dx+\int_{2}^{6}\int_{ \frac{3}{2}x-8}^{1}xy\,dy\,dx. \end{equation*} Ahora calculamos la integral (\ref{1}) \begin{eqnarray*} \iint_{D}xy\,dx\,dy &=&\int_{-5}^{1}\int_{- \frac{5}{6}y-\frac{13}{6}}^{\frac{2}{3}y+\frac{16}{3}}xy\,dx\,dy \\ &=&\int_{-5}^{1}\left. \dfrac{x^{2}}{2}y\right\vert _{-\frac{5}{6} y-\frac{13}{6}}^{\frac{2}{3}y+\frac{16}{3}}\,dy \\ &=&\int_{-5}^{1}\dfrac{y}{2}\left( \left( \dfrac{2}{3}y+\dfrac{16}{ 3}\right) ^{2}-\left( -\dfrac{5}{6}y-\dfrac{13}{6}\right) ^{2}\right) \,dy \\ &=&\int_{-5}^{1}\dfrac{y}{2}\left( -\dfrac{1}{4}y^{2}+\dfrac{7}{2} y+\dfrac{95}{4}\right) \,dy \\ &=&\int_{-5}^{1}-\dfrac{1}{8}y^{3}+\dfrac{7}{4}y^{2}+\dfrac{95}{8} y\,dy \\ &=&\left. -\dfrac{1}{32}y^{4}+\dfrac{7}{12}y^{3}+\dfrac{95}{16} y^{2}\right\vert _{-5}^{1} \\ &=&\left( -\dfrac{1}{32}\left( 1\right) ^{4}+\dfrac{7}{12}\left( 1\right) ^{3}+\dfrac{95}{16}\left( 1\right) ^{2}\right) -\left( -\dfrac{1}{32}\left( -5\right) ^{4}+\dfrac{7}{12}\left( -5\right) ^{3}+\dfrac{95}{16}\left( -5\right) ^{2}\right) \\ &=&\dfrac{623}{96}-\dfrac{5375}{96} \\ &=&-\dfrac{99}{2}. \end{eqnarray*}

2. Calcular \(\iint_{D}2y\,dx\,dy\) donde \(D\) es la región en el primer cuadrante comprendida entre los círculos con centro en el origen y radios \(2\) y \(6. \)

    

   Solución:

   El círculo con centro en el origen y radio \(2\) tiene ecuación \begin{equation*} x^{2}+y^{2}=4 \end{equation*} y el otro círculo \begin{equation*} x^{2}+y^{2}=36. \end{equation*} La región es de tipo 3.

    

   

    

   • Si consideramos a \(D\) como de tipo 1, dividimos la región de la siguiente manera:

      

     

      

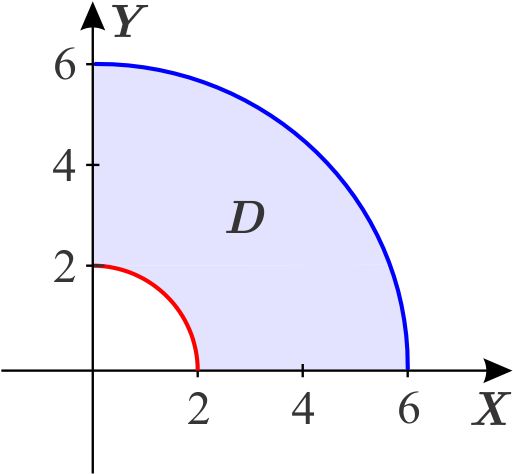
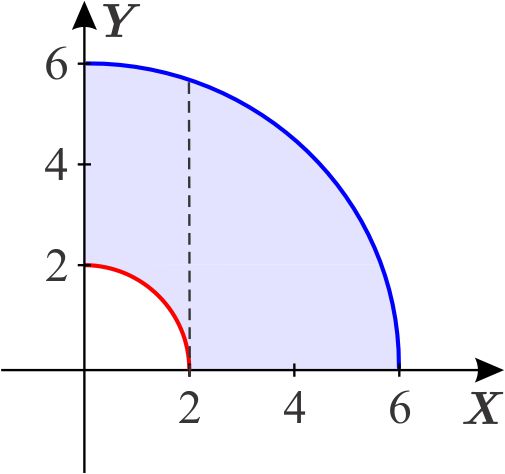
     Así \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{eqnarray*} D_{1} &=&\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 0,2\right] ,\quad \quad \sqrt{4-x^{2}}\leq y\leq \sqrt{36-x^{2}}\right. \right\} \\ D_{2} &=&\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 2,6\right] ,\quad \quad 0\leq y\leq \sqrt{36-x^{2}}\right. \right\} . \end{eqnarray*} Calculamos la integral: \begin{eqnarray*} \iint_{D}2y\,dx\,dy &=&\int_{0}^{2}\int_{\sqrt{ 4-x^{2}}}^{\sqrt{36-x^{2}}}2y\,dy\,dx+\int_{2}^{6}\int _{0}^{\sqrt{36-x^{2}}}2y\,dy\,dx \\ &=&\int_{0}^{2}\left. y^{2}\right\vert _{\sqrt{4-x^{2}}}^{\sqrt{ 36-x^{2}}}\,dx+\int_{2}^{6}\left. y^{2}\right\vert _{0}^{\sqrt{ 36-x^{2}}}\,dx \\ &=&\int_{0}^{2}36-x^{2}-\left( 4-x^{2}\right) \,dx+\int_{2}^{6}36-x^{2}\,dx \\ &=&\int_{0}^{2}32\,dx+\int_{2}^{6}36-x^{2}\,dx \\ &=&\left. 32x\right\vert _{0}^{2}+\left. 36x-\dfrac{x^{3}}{3}\right\vert _{2}^{6} \\ &=&32\left( 2\right) +36\left( 6-2\right) -\dfrac{1}{3}\left( 6^{3}-2^{3}\right) \\ &=&\dfrac{416}{3}. \end{eqnarray*}

   • Si consideramos a \(D\) como de tipo 2, dividimos la región de la siguiente manera:

      

     

      

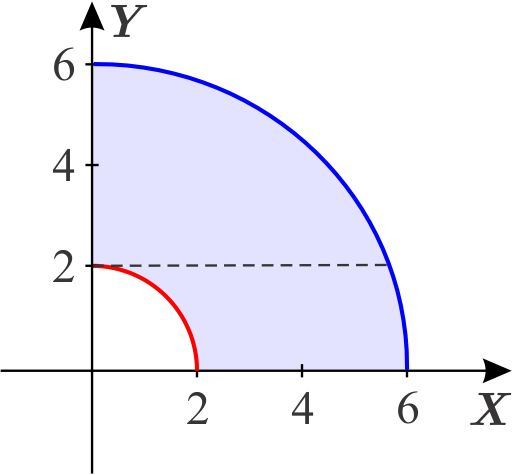
     Así \begin{equation*} D=D_{1}\cup D_{2}, \end{equation*} donde \begin{eqnarray*} D_{1} &=&\left\{ \left( x,y\right) \,\left\vert \,\,\,y\in \left[ 0,2\right] ,\quad \quad \sqrt{4-y^{2}}\leq x\leq \sqrt{36-y^{2}}\right. \right\} \\ D_{2} &=&\left\{ \left( x,y\right) \,\left\vert \,\,\,y\in \left[ 2,6\right] ,\quad \quad 0\leq x\leq \sqrt{36-y^{2}}\right. \right\} . \end{eqnarray*} Calculamos la integral \begin{eqnarray*} \iint_{D}2y\,dx\,dy &=&\int_{0}^{2}\left( \int_{\sqrt{4-y^{2}}}^{\sqrt{36-y^{2}}}2y\,dx\right) \,dy+\int_{2}^{6}\left( \int_{0}^{\sqrt{36-y^{2}} }2y\,dx\right) \,dy \\ &=&\int_{0}^{2}\left. 2xy\right\vert _{\sqrt{4-y^{2}}}^{\sqrt{ 36-y^{2}}}\,dy+\int_{2}^{6}\left. 2xy\right\vert _{0}^{\sqrt{ 36-y^{2}}}\,dy \\ &=&\int_{0}^{2}2y\sqrt{36-y^{2}}-2y\sqrt{4-y^{2}} \,dy+\int_{2}^{6}2y\sqrt{36-y^{2}}\,dy \\ &=&\left. -\dfrac{2\left( 36-y^{2}\right) ^{\frac{3}{2}}}{3}+\dfrac{2\left( 4-y^{2}\right) ^{\frac{3}{2}}}{3}\right\vert _{0}^{2}+\left. -\dfrac{2\left( 36-y^{2}\right) ^{\frac{3}{2}}}{3}\right\vert _{2}^{6} \\ &=&-\dfrac{2}{3}\sqrt{32^{3}}-\left( -\dfrac{2}{3}\sqrt{36^{3}}+\dfrac{2}{3} \sqrt{4^{3}}\right) +\dfrac{2}{3}\sqrt{32^{3}} \\ &=&\dfrac{416}{3}. \end{eqnarray*}

   Observamos que al describir la región \(D\) como de tipo 1 o 2, en cualquier caso, dividimos \(D\) en dos regiones, sin embargo, la integración resultó más sencilla al describirla como de tipo 1.

3. Calcular el área de la región \(D\) acotada por las gráficas de las rectas \(y=\dfrac{15}{14}x+\dfrac{37}{14}, \) \(y=\dfrac{1}{2}\) y la hipérbola \(xy=1. \)

    

   Solución:

   Escribimos la hipérbola como \(y=\dfrac{1}{x},\) dibujamos las tres curvas:

    

   

    

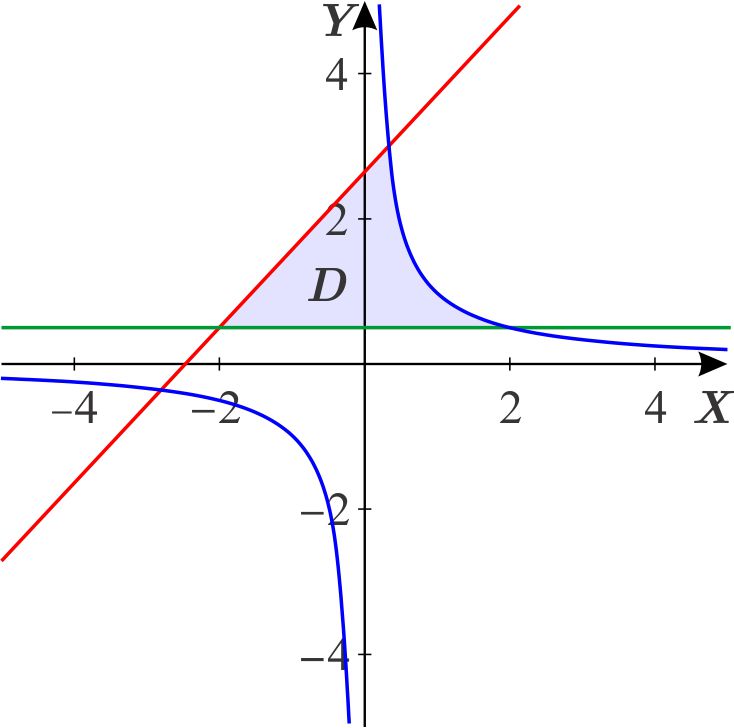
   Encontramos los puntos de intersección de las rectas y de cada una de ellas con la hipérbola: Primero determinamos el punto de intersección de las rectas. \begin{eqnarray*} \dfrac{15}{14}x+\dfrac{37}{14} &=&\dfrac{1}{2} \\ \dfrac{15}{14}x &=&\dfrac{1}{2}-\dfrac{37}{14} \\ \dfrac{15}{14}x &=&-\dfrac{15}{7} \\ x &=&-2. \end{eqnarray*} Es decir, las rectas se cortan en el punto de coordenadas \(\left( -2,\dfrac{1 }{2}\right) . \)

   Para determinar la intersección de la recta \(y=\dfrac{15}{14}x+\dfrac{37 }{14}\) con la hipérbola \(y=\dfrac{1}{x},\) resolvemos \begin{eqnarray*} \dfrac{15}{14}x+\dfrac{37}{14} &=&\dfrac{1}{x} \\ 15x^{2}+37x &=&14 \\ 15x^{2}+37x-14 &=&0 \\ \left( 5x+14\right) \left( 3x-1\right) &=&0, \end{eqnarray*} de donde \begin{equation*} x=-\dfrac{14}{5}\quad \quad \text{o} \quad \quad x=\dfrac{1}{3}. \end{equation*} Puesto que en la región a considerar únicamente interviene la rama derecha de la hipérbola, solamente consideramos \(\dfrac{1}{3},\) es decir, el punto de intersección es \(\left( \dfrac{1}{3},3\right) . \)

   Para determinar la intersección de la recta \(y=\dfrac{1}{2}\) con la hipérbola \(y=\dfrac{1}{x},\) resolvemos \begin{eqnarray*} \dfrac{1}{2} &=&\dfrac{1}{x} \\ x &=&2, \end{eqnarray*} de donde, el punto de intersección es \(\left( 2,\dfrac{1}{2}\right) . \) Dibujamos la región:

    

   

    

   • Como región de tipo 1 tenemos:

      

     

      

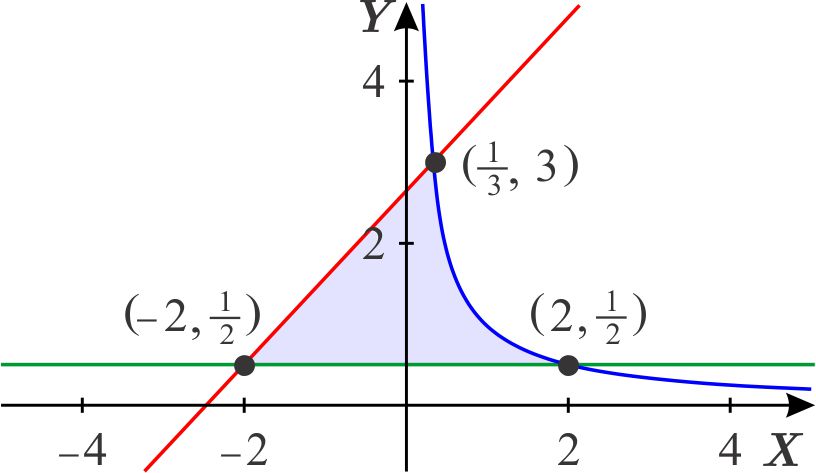
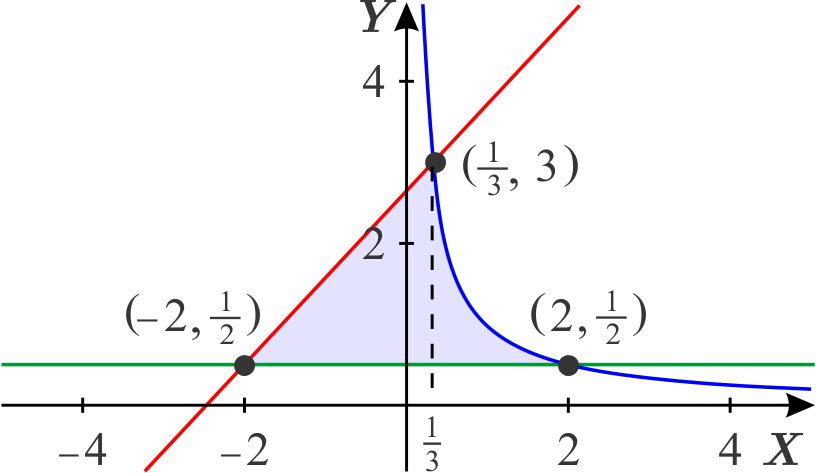
     donde \begin{eqnarray*} D_{1} &=&\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ -2,\dfrac{1}{3} \right] ,\quad \quad \dfrac{1}{2}\leq y\leq \dfrac{15}{14}x+\dfrac{37}{14} \right. \right\} \\ D_{2} &=&\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ \dfrac{1}{3},2 \right] ,\quad \quad \dfrac{1}{2}\leq y\leq \dfrac{1}{x}\right. \right\} . \end{eqnarray*} En este caso la región \(D\) considerada se escribe como \(D=D_{1}\cup D_{2}. \)

   • Para presentarla como región de tipo 2 despejamos \(x\) de las ecuaciones \(y=\dfrac{15}{14}x+\dfrac{37}{14}\) y \(y=\dfrac{1}{x} \): \begin{equation*} x=\dfrac{14}{15}y-\dfrac{37}{15} \end{equation*} y \begin{equation*} x=\dfrac{1}{y}, \end{equation*} entonces \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ \dfrac{1}{2},3\right] ,\quad \quad \dfrac{14}{15}y-\dfrac{37}{15}\leq x\leq \dfrac{1}{y}\right. \right\} . \end{equation*} Calculamos el área usando la descripción de la región como de tipo 2. \begin{eqnarray*} A &=&\iint_{D}dx\,dy \\ &=&\int_{\frac{1}{2}}^{3}\int_{\frac{14}{15}y-\frac{37}{ 15}}^{\frac{1}{y}}dx\,dy \\ &=&\int_{\frac{1}{2}}^{3}\dfrac{1}{y}-\dfrac{14}{15}y+\dfrac{37}{15 }\,dy \\ &=&\left. \ln y-\dfrac{7}{15}y^{2}+\dfrac{37}{15}y\right\vert _{\frac{1}{2} }^{3} \\ &=&\ln 3-\dfrac{7}{5}\left( 3\right) +\dfrac{37}{5}-\left( \ln \dfrac{1}{2}- \dfrac{7}{15}\left( \dfrac{1}{2}\right) ^{2}+\dfrac{37}{15}\left( \dfrac{1}{2 }\right) \right) \\ &=&\ln 6+\dfrac{25}{12}. \end{eqnarray*}

4. Evalúa la integral \(\int_{-1}^{1}\int_{0}^{ \sqrt{1-y}}xe^{y}\,dx\,dy\) cambiando el orden de integración.

   Solución:

   La región de integración \(D\) es de tipo 2: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,y\in \left[ -1,1\right] ,\quad \quad 0\leq x\leq \sqrt{1-y}\right. \right\} . \end{equation*} Despejamos \(y\) de la ecuación \(x=\sqrt{1-y} \): \begin{eqnarray*} x^{2} &=&1-y \\ -x^{2}+1 &=&y. \end{eqnarray*} La región es:

    

   

    

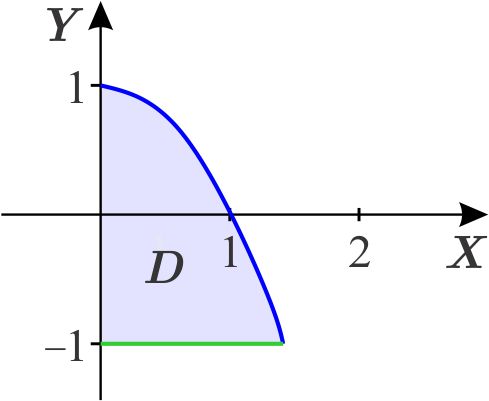
   Observamos que cuando \(y\) es igual a \(-1,\) \begin{equation*} x=\sqrt{2}. \end{equation*} Escribimos a \(D\) como región de tipo 1: \begin{equation*} D=\left\{ \left( x,y\right) \,\left\vert \,x\in \left[ 0,\sqrt{2}\right] ,\quad \quad -1\leq y\leq -x^{2}+1\right. \right\} , \end{equation*} de donde, \begin{eqnarray*} \int_{-1}^{1}\int_{0}^{\sqrt{1-y}}xe^{y}\,dx\,dy &=&\int_{0}^{\sqrt{2}}\int_{-1}^{-x^{2}+1}xe^{y}\,dy\,dx \\ &=&\int_{0}^{\sqrt{2}}\left. xe^{y}\right\vert _{-1}^{-x^{2}+1}\,dx \\ &=&\int_{0}^{\sqrt{2}}xe^{-x^{2}+1}-xe^{-1}\,dx \\ &=&\left. -\dfrac{1}{2}e^{-x^{2}+1}-\dfrac{x^{2}}{2}e^{-1}\right\vert _{0}^{ \sqrt{2}} \\ &=&-\dfrac{1}{2}e^{-2+1}-\dfrac{2}{2}e^{-1}-\left( -\dfrac{1}{2}e\right) \\ &=&-\dfrac{3}{2}e^{-1}+\dfrac{1}{2}e. \end{eqnarray*}

Ejercicios

1. Considera la región acotada por las gráficas de: la recta \( y=-2x+13\) y la parábola \(y=x^{2}-2x+4.\) Dibuja la región y encuentra su área. Verifica tu resultado cambiando el orden de integración.
2. Encuentra el área de la región acotada por \(x+2=\left( y-1\right) ^{2}\) y \(7y=-2x.\) Verifica tu resultado cambiando el orden de integración.
3. Encuentra el área de la región acotada por \(y=\dfrac{x^{2}}{4} , \) \(y=2\sqrt{x}\) y debajo de la recta que une los puntos \(\left( 1,2\right) \) y \(\left( 3,0\right) .\) Verifica tu resultado cambiando el orden de integración. Evalúa las siguientes integrales cambiando el orden de integración, ya que así es más sencillo calcularlas.
    
4. \(\int_{0}^{1}\int_{x}^{1}\sqrt{y^{2}+1}\,dy\,dx. \)
    
5. \(\int_{0}^{4}\int_{\sqrt{x}}^{2}\dfrac{4y^{2}}{ y^{5}+6}\,dy\,dx. \)
    
6. \(\int_{0}^{2}\int_{-\sqrt{x}}^{\sqrt{x} }y\,dy\,dx+\int_{2}^{4}\int_{-\sqrt{4-x}}^{\sqrt{4-x} }y\,dy\,dx \)
    
7. \(\int_{0}^{1}\int_{\text{arcsen}x}^{\frac{\pi }{ 2}}e^{\cos y}\,dy\,dx. \)
    
8. \(\int_{1}^{4}\int_{\sqrt[5]{x}}^{\sqrt{x}}e^{\frac{ x}{y^{2}}}\,dy\,dx+\int_{4}^{32}\int_{\sqrt[5]{x}}^{2}e^{ \frac{x}{y^{2}}}dy\,dx. \)
    
9. \(\int_{0}^{8}\int_{\sqrt[3]{x}}^{2}e^{y^{4}}\,dy \,dx. \)
    
10. \(\int_{0}^{1}\int_{\arctan y}^{-\frac{\pi }{4} \left( y-2\right) }y\,dx\,dy. \)