Hipótesis: Sea el triángulo ABC y sean AL una bisectriz interna, BM' y CN' las bisectrices externas de los otros dos ángulos.

Demostración.

P1.
Por el Teorema II.7.h, teorema de la bisectriz, sabemos que la bisectriz interna AL divide al lado opuesto BC, y es tal que satisface .

P2.
Por el mismo Teorema, la bisectriz externa BM' divide al lado opuesto CA, y es tal que satisface .

P3.
Igualmente, la bisectriz externa CN' divide al lado opuesto AB, y es tal que satisface .

P4.
Multiplicando miembro a miembro (1), (2) y (3) obtenemos
.

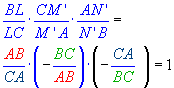Por lo tanto, .

Por el Teorema II.7.e, recíproco del teorema de Ceva, se sigue que las bisectrices AL, BM' y CN' se intersectan.

Q.E.D.