Reescribiendo la proposición I.34 en lenguaje actual:

I.34  En todo paralelogramo los lados y los ángulos opuestos son iguales, y la diagonal divide el área del paralelogramo en dos áreas iguales.

Hipótesis: Sea ABCD un paralelogramo, y BC su diagonal.

Demostración.

P1.
Como AB es paralela a CD, y la recta BC es transversal a ellas, por la Proposición I.29, tenemos que los ángulos alternos y son iguales entre sí.
Es decir, .

P2.
Nuevamente, como AC es paralela a BD, y BC es transversal a ellas, por la Proposición I.29, tenemos que los ángulos alternos y son iguales entre sí.
Es decir, .

P3.
Por lo tanto, y son dos triángulos que tienen los dos ángulos y igual a los dos ángulos y , respectivamente, y el lado BC colinda con los ángulos iguales y es común a ambos.
Por la Proposición I.26, se sigue que los triángulos tienen los lados restantes iguales a los lados restantes, respectivamente, y el ángulo restante igual al ángulo restante, y en consecuencia, los triángulos y son iguales.
Por lo tanto,
.

P4.
Como = y
= , por la Noción común 2, el ángulo = .
Por lo tanto, .

P5.
Resumiendo,
,
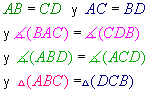Por lo tanto, en todo paralelogramo los lados y los ángulos opuestos son iguales entre sí.

P6.
Como consecuencia de trazar la diagonal BC, en el paso 3, concluimos que los triángulos y son iguales. Por lo tanto, la diagonal BC divide el área del paralelogramo en dos áreas iguales.

Por lo tanto, en todo paralelogramo los lados y los ángulos opuestos son iguales, y la diagonal divide el área en dos partes iguales.

Q.E.D.