Coordenadas Cilíndricas y Esféricas

Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\)

\(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Obtén la ecuación en coordenadas rectangulares de la superficie \( S \) cuya ecuación esférica es \( \rho =12\cos \phi . \)

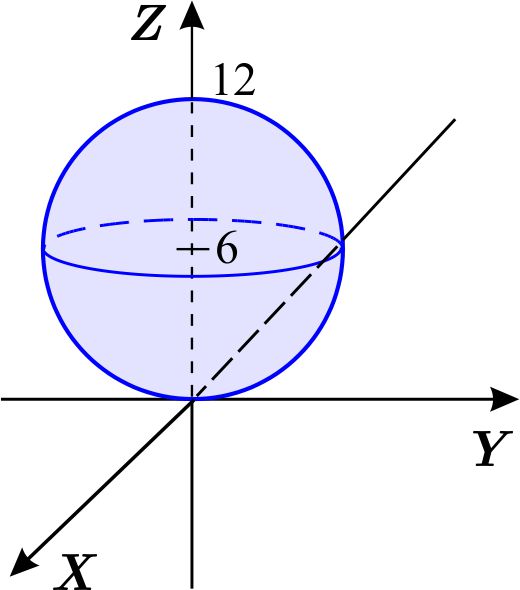
Solución:

\[ \rho =12\cos \phi \] Sustituimos \(\cos \phi =\frac{z}{\rho }\) \[ \rho ^{2} = 12z \] ahora sustituimos \(\rho^{2}=x^{2}+y^{2}+z^{2}\) \[ x^{2}+y^{2}+z^{2}=12z \] pasamos todo del lado izquierdo y completamos el trinomio cuadrado perfecto \begin{eqnarray*} x^{2}+y^{2}+z^{2}-12z &=&0 \\ x^{2}+y^{2}+z^{2}-12z+6^{2} &=&36 \\ x^{2}+y^{2}+\left( z-6\right) ^{2} &=&36 \end{eqnarray*} Por tanto, \( S \) es una esfera con centro en \( \left( 0,0,6\right) \) y radio \( 6. \)

Universidad Nacional Autónoma de México