Coordenadas Cilíndricas y Esféricas Angel Carrillo Hoyo, Elena de Oteyza de Oteyza\(^2\), Carlos Hernández Garciadiego\(^1\), Emma Lam Osnaya\(^2\) \(^1\) Instituto de Matemáticas, UNAM; \(^2\) Facultad de Ciencias, UNAM

Obtén la ecuación esférica del manto superior del cono circular de dos mantos \( S \) cuya ecuación rectangular es \( x^{2}+y^{2}- \dfrac{z^{2}}{4}=0. \)

Solución:

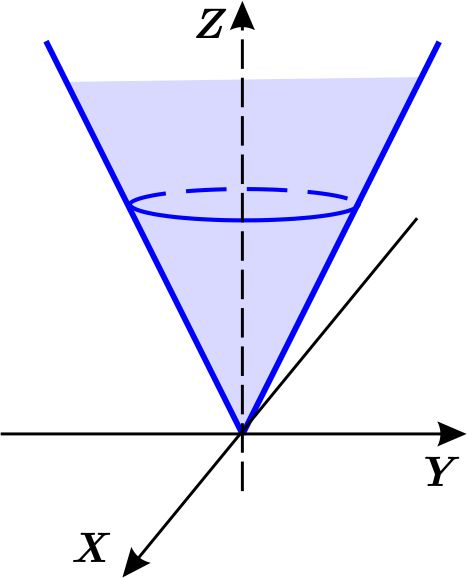
Como \( x^{2}+y^{2}=\rho ^{2}\ \text{sen}\ ^{2}\phi \) y \( z=\rho \cos \phi \) entonces la ecuación \( x^{2}+y^{2}-\dfrac{z^{2}}{4}=0 \) se transforma en \begin{eqnarray*} \rho ^{2}\ \text{sen}\ ^{2}\phi &=&\dfrac{\rho ^{2}\cos ^{2}\phi }{4} \\ \tan ^{2}\phi &=&\dfrac{1}{4} \\ \left\vert \tan \phi \right\vert &=&\dfrac{1}{2}. \end{eqnarray*} Como estamos interesados en el manto superior, entonces \( 0<\phi <\dfrac{\pi }{2}. \) La función \( \tan \) es no negativa en \( \left[ 0,\dfrac{\pi }{2} \right) , \) por lo que \begin{eqnarray*} \left\vert \tan \phi \right\vert &=&\tan \phi =\dfrac{1}{2} \\ \phi &=&\arctan \dfrac{1}{2}. \end{eqnarray*}