Segundo teorema fundamental

En este apartado podrás encontrar el segundo teorema fundamental del cálculo y algunas de sus consecuencias.

Es aquí que requerirás de manera importante el Teorema del valor medio para derivadas. Conviene que lo revises antes de entrar en materia. En la demostración nos referiremos a este teorema como TVM.

Teorema 2 (Segundo teorema fundamental del cálculo infinitesimal)



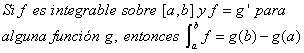
Observaciones

1. Este teorema tiene mucho parecido al Corolario del Primer teorema fundamental. La conclusión es la misma.
2. Sin embargo, en una de las hipótesis hay una diferencia importante. En el corolario se pide que f sea continua en [a,b], en cambio en este segundo teorema, sólo se pide que f sea integrable.
3. Ya sabemos que si f es continua en [a,b], es integrable, pero el recíproco no es cierto. ¿Recuerdas?.
4. Por tanto este segundo teorema fundamental, es más fuerte que el corolario. Lo incluye.

Ejemplos

A continuación te presentamos un par de ejemplos sencillos, pero ilustrattivos, de funciones integrables, que no son continua, pero a las cuales se les puede aplicar el segundo teorema fundamental.

Es evidente que este segundo teorema fundamental también se aplica a funciones continuas (ya que son integrables), pero para ellas, basta el Corolario del primer teorema fundamental.