El número e y la exponencial
En este apartado encontrarás la relación entre el número exp(1) y la función exponencial. Igualmente encontrarás las primeras aproximaciones para dicho número y la gráfica de la función exponencial, relacionada con la de su inversa, log(x).
El número exp(1), adquiere ahora mayor interés y habrá que precisar su valor. Sabemos que es un real, pero ¿será racional o irracional?. Por lo pronto, le asignaremos un nombre más corto.
Definición
Es decir el número e, es aquel para el cual log(e) = 1. En otras palabras:
Si mueves el punto rojo x, cuando la integral vale 1, entonces x = e.
(desde luego que en el interactivo nos dará un valor aproximado)
i.e. 
Queda la duda sobre el valor del número e. Para empezar haremos ver que: 
, lo cual no es muy halagüeño, pero con las herramientas teóricas que tenemos hasta ahora, es lo que podemos lograr. Veamos:
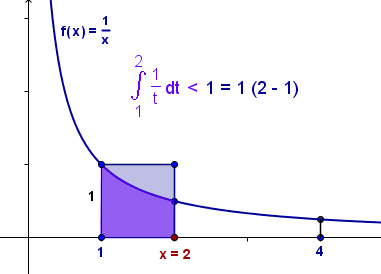
El área del cuadrado en azul es mayor que el área bajo la curva.
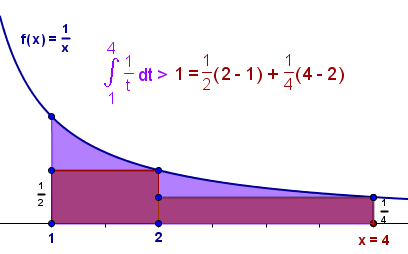
La suma de las áreas de los rectángulos en rojo,
es
menor que
el área bajo la curva.
Es decir:
Consecuentes con el trabajo de las propiedades de los exponentes para números racionales, definiremos, la exponencial en términos del número e = exp(1), de la siguiente manera:
Definición
Observaciones
