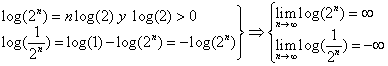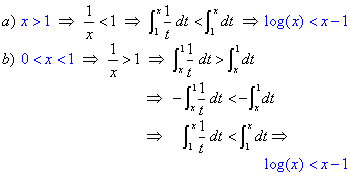La función logaritmo

En este apartado encontrarás la definición de la función logaritmo y la demostración de sus propiedades más importantes. Con lo anterior allanaremos el camino para definir la función exponencial y para la demostración igualmente de sus propiedades más importantes.

Definición

Puedes mover x y observar que: a) log(x) < 0 para 0< x < 1,
b) log(x) = 0 para x = 1 y c) log(x) > 0 para x > 1.

Estas propiedades corresponden a las propiedades de la integral que hemos visto con anticipación. Por ejemplo a), corresponde a la propiedad .

Por otra parte log(x) no es posible definirlo para , puesto que no está acotada en el intervalo .
Ahora estamos en posibilidad de demostrar una de las propiedades más importantes de la función logaritmo, a saber:

Teorema 1

A partir de este teorema tenemos dos resultados particulares de interés.

Corolario 1

Corolario 2

Análisis primario de log(x)

1. Por el teorema fundamental del cálculo, tenemos que , lo cual significa que log(x) es creciente.
2. Como , significa que el crecimiento de log(x) es cada vez menor, conforme x crece.
3. A pesar de ello, log(x) no está acotada, ni superior, ni inferiormente, puesto que:
4. Por tanto . Esto último nos indica que .
5. Como , entonces log(x) es asintótica al eje negativo de las y.
6. Como , entonces log(x) es cóncava.
7. Y por último , puesto que:
   
   

Clic para ir al interactivo