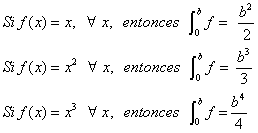
Entonces por el Teorema 4, tenemos que

Ejemplos y observaciones
En
este apartado encontrarás algunos ejemplos que son posibles a partir de la aplicación de los teoremas hasta ahora vistos.
Hemos visto que
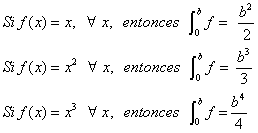
Entonces por el Teorema 4, tenemos que

Por otra parte hemos visto que
Una función discontinua de primera clase (o con discontinuidad removible) es integrable, como por ejemplo
![]()

¿La recuerdas? Si no puedes ir a los ejemplos del Criterio de Integrabilidad o dar clic aquí.
Utilizando el Teorema 5, podemos extender la integrabilidad
Podemos hacer ver que una función continua en un intervalo cerrado, excepto en uno de sus puntos, en donde tiene una discontinuidad de segunda clase (o no removible), es integrable sobre [a,b].
Por ejemplo, la función
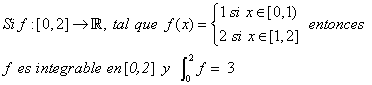
La razón es que es integrable sobre [0,1] y sobre [1,2], entonces, por el teorema 5 es integrable en [0,2] y la integral es fácil de calcular. ¿Puedes ingeniar otras funciones discontinuas de primera y segunda clase que sean integrables?.
El Teorema 7, nos permite tener una idea entre que valores está la integral
Algunas veces resulta muy difícil calcular una integral, entonces poder aproximarla aunque sea de manera burda, será un avance. Para ver un ejemplo, puedes dar clic aquí
Sobre la notación
Hasta ahora hemos utilizado una notación muy cómoda y económica para la integral: ![]() . Esto es porque en nuestras expresiones hasta sólo hemos manejado una sóla variable. Cuando en una expresión hay más de una variable, entonces es necesario hacer explícita la variable de integración y en ese caso, las otras se comportan como constantes respecto a ésta. Por ejemplo:
. Esto es porque en nuestras expresiones hasta sólo hemos manejado una sóla variable. Cuando en una expresión hay más de una variable, entonces es necesario hacer explícita la variable de integración y en ese caso, las otras se comportan como constantes respecto a ésta. Por ejemplo:
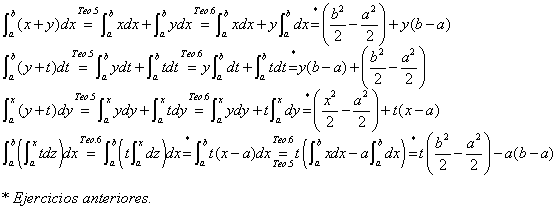
Un detalle más sobre la notación
Las integrales a continuación, significan lo mismo
![]()