Proposición 1-
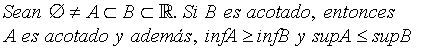
El ínfimo del subconjunto A, es mayor que el ínfimo del conjunto B que lo contiene y el supremo del subconjunto A es menor que el supremo del conjunto B que lo contiene.
Conceptos previos
Para comprender mejor la construcción del concepto de Integral, es muy importante que tengas claros los conceptos de ínfimo y supremo, relacionados por supuesto con conjuntos acotados y con el axioma del supremo, vistos en el curso de Cálculo Diferencial e Integral I. También debes tener claro el significado de función acotada y el concepto de partición de un intervalo cerrado, que incluiremos en esta sección.
Ínfimo y Supremo de un conjunto
Si deseas recordar estos conceptos, da clic aquí.
Función acotada
Si deseas recordar, da clic aquí.
Algunas proposiciones
Para tener presentes algunos resultados que se utilizan casi de inmediato en este apartado, incluimos las siguientes proposiciones.
Proposición 1-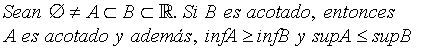
El ínfimo del subconjunto A, es mayor que el ínfimo del conjunto B que lo contiene y el supremo del subconjunto A es menor que el supremo del conjunto B que lo contiene.
Proposición 2-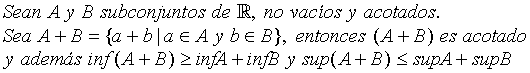 
Estas proposiciones serán de mucha utilidad, la primera para la construcción del concepto de integral y la segunda, en los teoremas de álgebra de las funciones integrables. Te conviene tenerlos en cuenta.
Proposición 3- 
Los siguientes tres resultados te permitirán calcular tus primeras integrales, por medio de la definición.
Proposición 4 -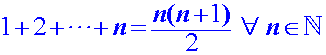 
Proposición 5 - 
Proposición 6 - 
El concepto de límite lo debes tener muy bien asimilado.
Definición de límite - 
Ya por último te recomenamos tener claro el Teorema del Valor Medio para Derivadas.
Teorema del Valor Medio - 
Partición de un intervalo [a,b]
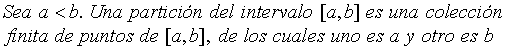
Como se trata de un conjunto finito de puntos, estos pueden ser numerados y ordenados como:
Así es que pensaremos en una partición, como un conjunto finito y ordenado de puntos, donde el primero es a y el último es b. Es decir que siempre pensaremos en que a < b.
Para reflexionar
