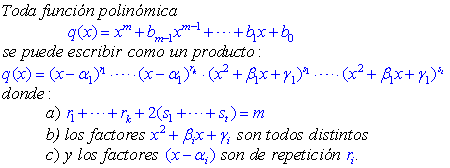
Integración por fracciones parciales
En este apartado encontrarás un método para integrar cocientes de funciones polinomiales, también llamadas funciones racionales. La justificación teórica de dicho método se basa en el Teorema Fundamental del Álgebra y en otros resultados que se desarrollan en el estudio de las funciones complejas.
Por lo anterior, sólo exhibiremos los teoremas correspondientes, sin su demostración y lo que sí, desarrollaremos diversos ejemplos que permitan entender este método de integración por fracciones parciales.
Teorema 1 (Descomposición de un polinomio en factores reales y complejos)
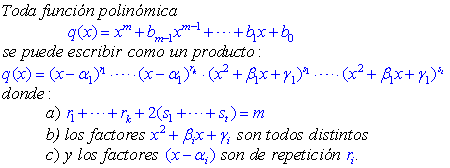
Es decir que toda función polinómica se puede escribir como un producto de factores reales y complejos. Los factores reales pueden ser con repetición y los factores complejos son por pares y distintos.
Teorema 2 (Descomposición de un cociente de polinomios en fracciones parciales)
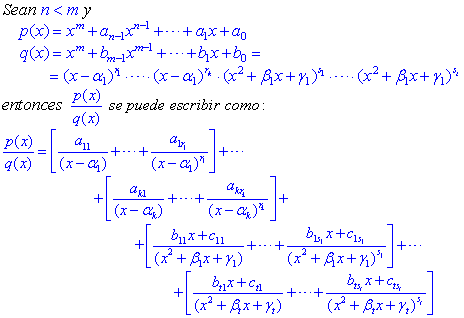
Es decir:
Por ejemplo
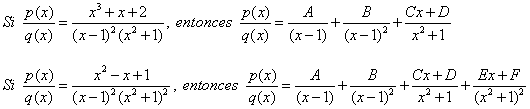
Y claro, el problema es calcular las incógnitas A, B, C, D y en su caso E y F. Desde luego el teorema 2, asegura que existe solución.
El método de integración
La posibilidad que proporciona el Teorema 2, de descomponer el cociente de polinomios en fracciones, permite calcular la integral de dicho cociente como una suma de integrales de dichas fracciones, las cuales son realmente sencillas de obtener.
Ejemplos
En los ejemplos que presentamos, consideraremos por separado los cuatro casos posibles:

En caso que existan combinaciones, que es lo más probable, se aplica lo correspondiente a cada caso.
Igualmente en los ejemplos que presentamos haremos énfasis en el cálculo de las fracciones parciales y dejaremos indicadas las integrales correspondientes.
En los siguientes ejemplos, ilustramos el caso a) en
el
cual, el denominador tiene raíces reales simples.
En los siguientes ejemplos, ilustramos el caso b) en
el cual, el denominador tiene raíces reales repetidas.
En los siguientes ejemplos, ilustramos el caso c) en
el cual, el denominador tiene raíces complejas simples.
En los siguientes ejemplos, ilustramos el caso d) en
el cual, el denominador tiene raíces complejas repetidas.
En general las integrales que resultan después de aplicar este método de fracciones parciales, son mucho más sencillas, así justificamos el haberlas dejado indicadas.
En el siguiente apartado, veremos algunos casos de reducción de integrales a casos más sencillos, mediante fórmulas llamadas de reducción.