Funciones coseno y seno

En este apartado encontrarás la definición de la función coseno en términos del área del sector circular y la definición de la función seno. Además encontrarás algunos teoremas, relacionados con sus derivadas.

Para iniciar, estableceremos la definición para y luego la extenderemos a todos los reales. En la definición siguiente es importante recordar que la función área es uno a uno y además que el área del sector circular en términos del arco x es .

Definición

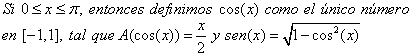
Observaciones

a) La función coseno está bien definida puesto que la función área es inyectiva. No puede haber una x que tenga dos valores cos(x).

b) La función seno también está bien definida, puesto que y por tanto su raíz es real.

c) De la definición del coseno, tenemos que y por tanto, las funciones 2A y coseno, son inversas. Esta propiedad será necesario tenerla en cuenta en la demostración de nuestro siguiente teorema.

Antes, enunciaremos un lema (sin demostración) sobre la derivada de la inversa de una función, que de aquí en adelante será súmamente utilizado.

Lema 1 (la derivada de la inversa)

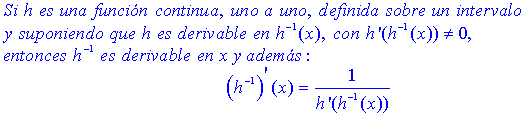
Teorema 1 (Derivada de las funciones coseno y seno)

Análisis de la función cos(x)

Utilizando lo ya visto, haremos un análisis de la función coseno, para hacer ver que su gráfica en es la siguiente:

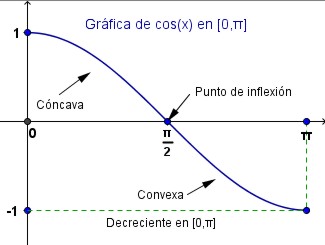
Clic sobre la gráfica para ver el análisis

Análisis de la función sen(x)

Similarmente, haremos un análisis de la función seno, para ver que su gráfica en es la siguiente:

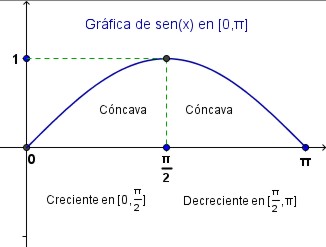
Clic sobre la gráfica para ver el análisis

Falta extender la definición a todos los reales. Para ello establecemos la siguiente

Definición

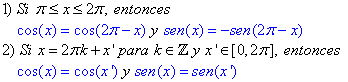
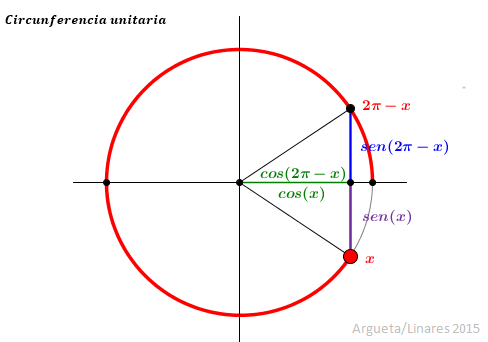
Clic para ir a interactivo para el caso

Extensión del Teorema 1 (Derivada de las funciones seno y coseno)

Observación

Para el caso de la definición anterior, las funciones seno y coseno toman los mismos valores, así que el teorema 1 queda obvio.

 

---