Para calcular el área del sector circular, trataremos dos casos:
Caso
. El área del sector circular se obtiene de sumar el área del tríangulo, más el área de la región en verde, representada por la integral de 
de t a 1, es: 
(2)Área del sector circular
Ahora podremos calcular el área del sector circular, pero con respecto a la abscisa del punto que define el rayo terminal del ángulo.
Dos casos a tratar
Para calcular el área del sector circular, trataremos dos casos:
Caso . El área del sector circular se obtiene de sumar el área del tríangulo, más el área de la región en verde, representada por la integral de de t a 1, es: (2)
Caso 
. El área del sector circular se obtiene restando el área del tríangulo del área de la región en verde, representada por la integral de de t a 1, es: (3)
Es importante hacer notar que como en este caso t es negativo o cero, la expresión 
es negativa o cero respectivamente.
Clic para ir a interactivo
Las expresiones (2) y (3) son la misma, en lo que difieren en cada caso, es en el signo de t, pero la fórmula para obtener el área del sector circular es la misma y además queda en función de t. Por lo tanto
Definición
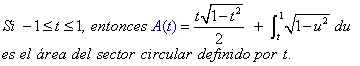
Análisis de A(t)
1) A(t) es continua en el intervalo [-1,1]. El primer sumando es producto de continuas y para la continuidad del segundo sumando basta recordar el primer teorema fundamental del cálculo.
2) A(t) es derivable en el intervalo (-1,1). El primer sumando es producto de derivables y para la derivabilidad del segundo sumando basta recordar el primer teorema fundamental del cálculo.
3) Por otra parte 
4) Además 
5) Y por otro lado 
6) Así,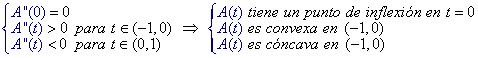 
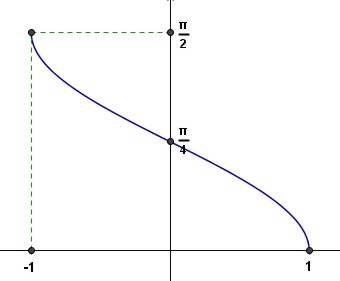
7) Finalmente 
, es continua, uno a uno, convexa en (-1,0) y cóncava en (0,1) y su gráfica es la siguiente:
