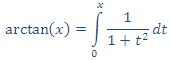
Polinomio de Taylor de arctan(x)

Cuando una función f es n veces derivable en un punto a, el Corolario del apartado anterior, nos ofrece un método útil para calcular su polinomio de Taylor en a. Ilustraremos este hecho con la función f(x) = arctan(x).

Procedimiento paso a paso

1. Recordemos que: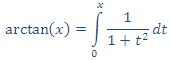

2. Calculando el cociente del integrando con todo y resto, nos queda:

3. De donde:

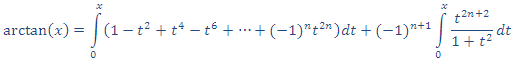
4. Realizando la integral sumando por sumando, excepto el último, nos queda:

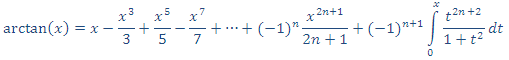
5. De acuerdo con el Corolario, el polinomio:

sería el polinomio de Taylor de grado 2n+1 en 0, para f(x)=arctan(x) siempre que:

6. Como: 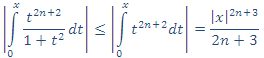, entonces:

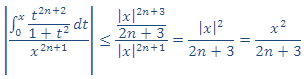
7. Y como: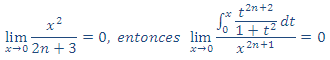

8. Entonces: es el polinomio de Taylor de f(x)=arctan(x) de grado 2n+1, en 0.

9. Volviendo a la desigualdad del punto 6:

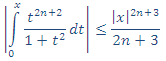
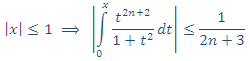
10. Como , entonces 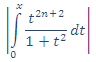se puede hacer tan pequeño como se quiera, haciendo n suficientemente grande.

Es decir, entre mayor sea el grado del polinomio de Taylor, más parecido será a la función f(x)=arctan(x).

En el siguiente apartado, trataremos de extender estas ideas a otras funciones y haremos el análisis de los polinomios de Taylor, con relación a su grado.