En este apartado encontrarás la definición del
que cumpla ciertas características y algunos de los ejemplos más sencillos.Polinomio de Taylor
En este apartado encontrarás la definición del que cumpla ciertas características y algunos de los ejemplos más sencillos.
Importante recordar
Para la siguiente definición, será importante recordar del apartado anterior, que si:
es un polinomio de grado n en (x - a), entonces los coeficientes tienen la siguiente expresión:
(3)
Definición (Polinomio de Taylor de grado n para f en a)
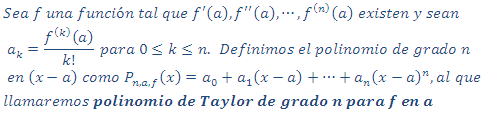
Surge una pregunta
Una primera pregunta que podría surgir, es la siguiente:
El resultado siguiente nos dará una primera respuesta:
Proposición 0
Es decir,
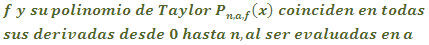
Ejemplos
Calcularemos el Polinomio de Taylor para funciones más o menos sencillas, pero también veremos algún caso con complicaciones, lo cual nos llevará a buscar métodos alternativos.
Una primera función para la cual es relativamente fácil
calcular su
.
Sabemos
que existen todas sus derivadas hasta el orden n y son ella misma.
 |
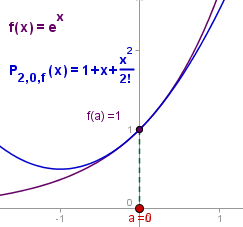
Otro ejemplo mas o menos sencillo es la función seno, de la cual
sabemos que es
derivable siempre y se puede evaluar fácilmente en 0.
 |
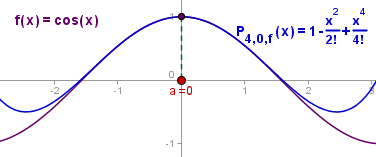
Otro ejemplo mas o menos sencillo es la función coseno, de la cual
sabemos que es derivable siempre y se puede evaluar fácilmente en 0.
 |
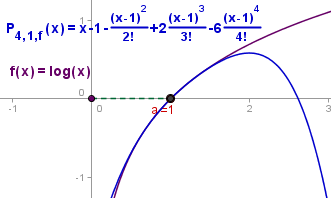
Otros ejemplo mas o menos sencillo es log(x) que igualmente es n veces derivable,
pero al no estar definida en 0, haremos el cálculo de su polinomio de Taylor en 1.
 |
Con el mismo método del ejemplo anterior te será posible descubrir que:
 |
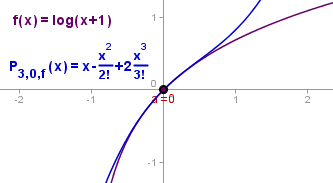
Un ejemplo complicado, que nos obliga a buscar métodos alternativos.
 |
En lo subsecuente necesitaremos construir la teoría necesaria para resolver casos como el anterior u otros.
