Introducción
Entre todas las funciones que se estudian en Cálculo Diferencial e Integral, las polinomiales son las más sencillas de todas. Los procedimientos para el cálculo de límites, para derivarlas o para integrarlas son bastante fáciles. Pero aún para evaluarlas en cualquier punto, se reducen a un número finito de multiplicaciones y adiciones.
En cambio el cálculo en otras funciones, como las logarítmicas, exponenciales, racionales o trigonométricas o combinaciones de ellas, pueden adquirir tintes de gran dificultad. Por ejemplo, si queremos calcular ![]() al menos no resulta inmediato.
al menos no resulta inmediato.
Ya en capítulos anteriores vimos las dificultades que se tienen para funciones que nos son polinómicas el cálculo de límites o de derivadas, por ejemplo![]() . Estas dificultades no están ausentes en el cálculo de integrales y es por todo esto que se destaca la importancia de poder aproximar funciones mediante funciones polinomiales.
. Estas dificultades no están ausentes en el cálculo de integrales y es por todo esto que se destaca la importancia de poder aproximar funciones mediante funciones polinomiales.
Una propiedad de los Polinomios
Antes de incursionar en la teoría para aproximar funciones por medio de funciones polinomiales, estudiemos una propiedad particular estas.
Sea ![]() una función polinomial de grado n y con dominio en los reales.
una función polinomial de grado n y con dominio en los reales.
Lo primero que podemos observar es que ![]() .
.
Derivando, tenemos ![]() , de donde:
, de donde: ![]()
Derivando nuevamente, tenemos ![]() , de donde:
, de donde: ![]()
Volviendo a derivar, nos queda ![]() , de donde:
, de donde: ![]()
Derivando una vez más, tenemos ![]() , de donde:
, de donde: ![]()
Podemos observar en general que:
![]() para
para ![]() ,
,
asumiendo que: ![]() .
.
Es decir, los coeficientes del polinomio se pueden escribir de la siguiente forma:
![]() asumiendo que:
asumiendo que: ![]() (1)
(1)
En resumen
En resumen un polinomio de grado n, lo podemos escribir de la siguiente forma:
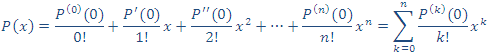 (2)
(2)
Es fácil observar que si:
![]() , entonces:
, entonces:
![]() (3)
(3)
con las mismas suposiciones anteriores: ![]() .
.
En el siguiente apartado será muy importante tener en cuenta las expresiones (1), (2) y (3).