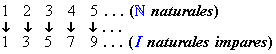
Para saber si dos conjuntos finitos A y B, tienen la misma cantidad de elementos, bastaría hacer corresponder cada uno de los elementos de A con cada uno de los de B y si no sobra ningún elemento, se concluye que si tienen la misma cantidad de elementos.
Este método, consiste matemáticamente en establecer una relación biyectiva (uno a uno y sobre) entre A y B, el cual se puede extender a conjuntos infinitos, de la siguiente manera:
Definición
Dos
conjuntos infinitos A y B, tienen la misma cardinalidad si entre ellos se
puede establecer una relación biyectiva.
Notación
Denotaremos por #(A) la cardinalidad del conjunto A.
El
todo no siempre es mayor que las partes
Dando
clic en Proposición
r1, verás la demostración
de que: Los impares positivos tienen la misma cardinalidad que los Naturales.
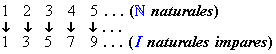
Dando clic en Proposición r2, verás la demostración de que: Los pares positivos tienen la misma cardinalidad que los Naturales.
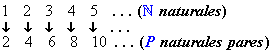
Así, no obstante que los naturales impares y los naturales pares son subconjuntos propios de los naturales, tenemos que: ![]() .
.
Una importante reflexión
Un subconjunto puede tener la misma cardinalidad del conjunto que lo contiene, pero nunca mayor, ¿Puedes explicarlo?. Así, podemos entender que: ![]() . Más adelante haremos ver que la igualdad no puede ser.
. Más adelante haremos ver que la igualdad no puede ser.
Los
Naturales y los Enteros tienen la misma Cardinalidad: ![]()
Dando
clic en Proposición
r3, verás su demostración.
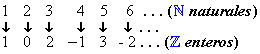
Los
Enteros y los Racionales tienen la misma Cardinalidad: ![]()
Dando
clic en Proposición r4, verás la ilustración
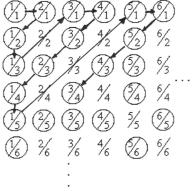
de la relación biyectiva entre los Naturales y los racionales positivos
(por las proposiciones anteriores con eso basta). El método consiste
en ir relacionando los naturales con los racionales en forma diagonal.
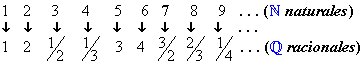
La
cardinalidad de los Racionales es menor que la Cardinalidad de los Reales: ![]()
Basta
demostrar que no es posible establecer una relación sobre entre los naturales y los reales del
intervalo [0,1].
Daremos
dos demostraciones.
Dando
clic en Proposición
r5, verás la primera demostración.
Para la segunda demostración partiremos del siguiente resultado que llamaremos:
R1.- La intersección de intervalos cerrados anidados y no vacíos,
es no vacía.
Da clic en su enunciado para ver la idea de su demostración.
Dando clic en Proposición r6, verás la segunda demostración.
Observaciones
muy importantes
Los
naturales, los enteros y los racionales por tener la misma cardinalidad,
se dice que son conjuntos numerables.
Cualquier
subconjunto infinito de los naturales tiene la cardinalidad de los naturales.
Todo
conjunto numerable tiene la misma cardinalidad que los naturales.
Los
irracionales y por tanto los reales, son conjuntos no numerables.
Conclusiones
En resumen, tenemos que:
![]()